Vorbehalte bei der Korrelation
Einführung in die Statistik in Python

Maggie Matsui
Content Developer, DataCamp
Nicht-lineare Beziehungen
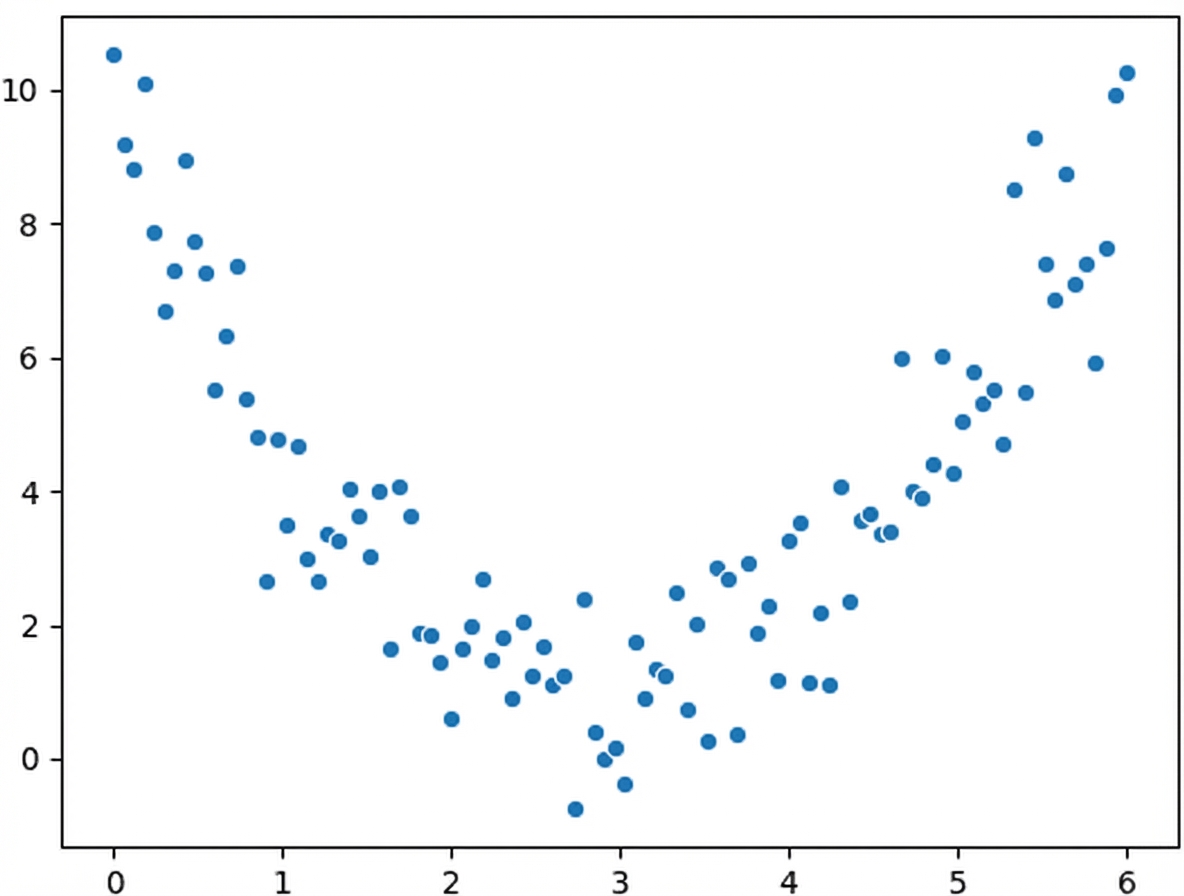
$$r = 0.18$$
Nicht-lineare Beziehungen
Was wir sehen:
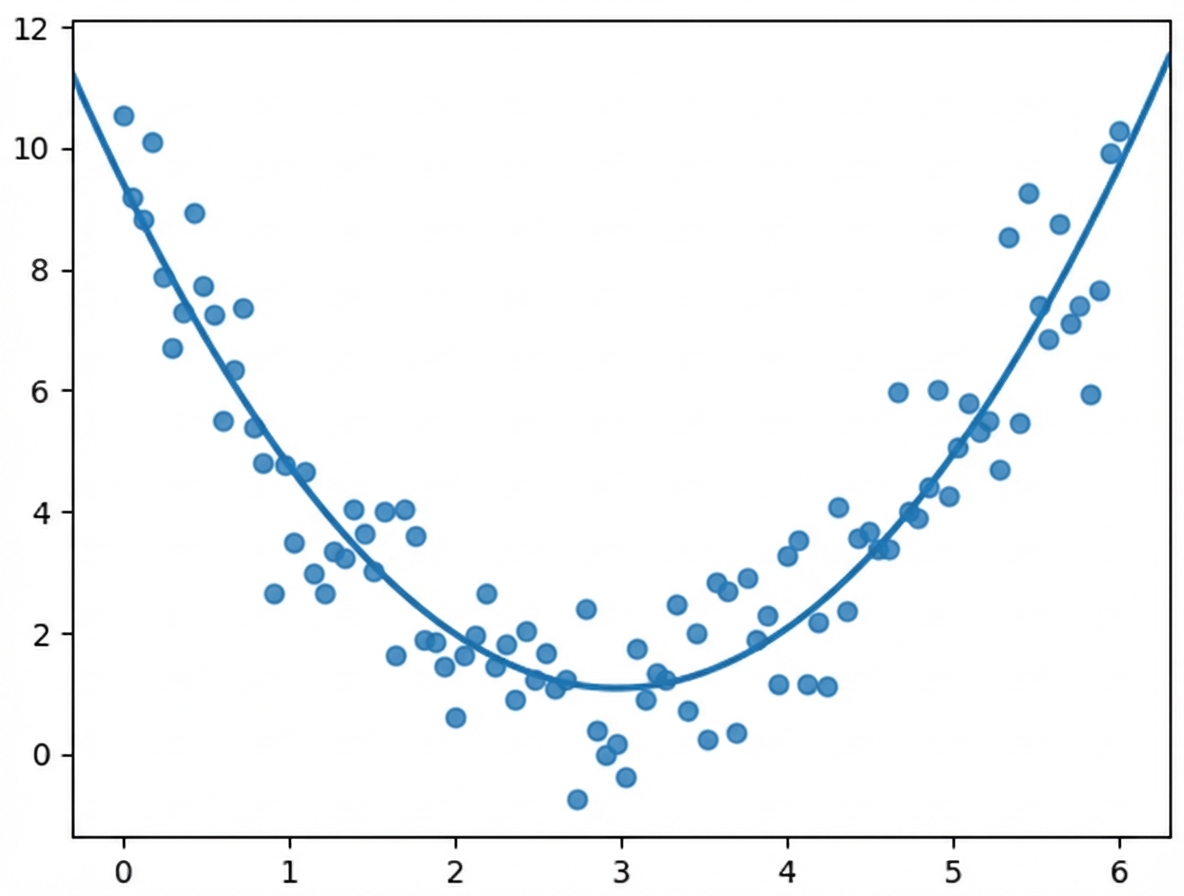
Was der Korrelationskoeffizient sieht:
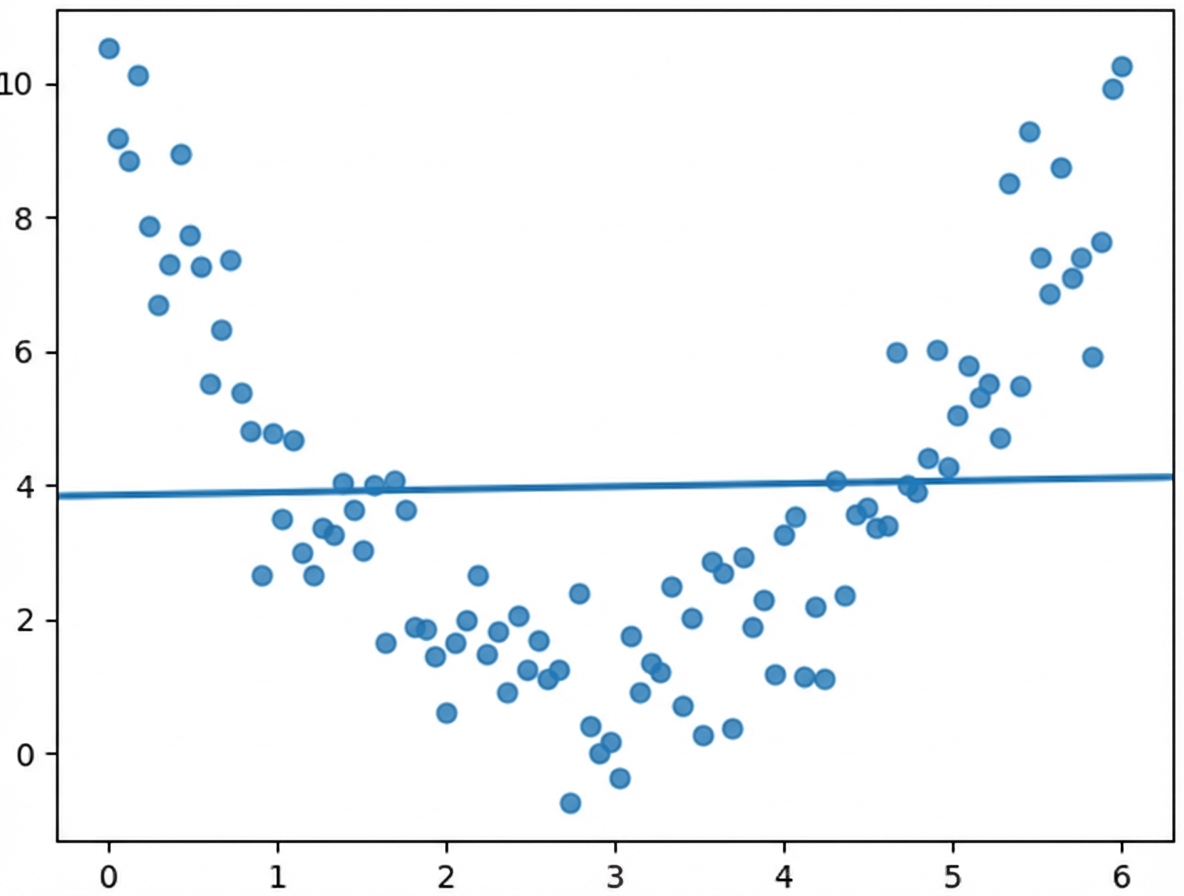
Die Korrelation berücksichtigt nur lineare Beziehungen
Korrelation sollte nicht blind verwendet werden
df['x'].corr(df['y'])
0.081094
Visualisiere deine Daten immer

Daten zum Schlaf von Säugetieren
print(msleep)
name genus vore order ... sleep_cycle awake brainwt bodywt
1 Cheetah Acinonyx carni Carnivora ... NaN 11.9 NaN 50.000
2 Owl monkey Aotus omni Primates ... NaN 7.0 0.01550 0.480
3 Mountain beaver Aplodontia herbi Rodentia ... NaN 9.6 NaN 1.350
4 Greater short-ta... Blarina omni Soricomorpha ... 0.133333 9.1 0.00029 0.019
5 Cow Bos herbi Artiodactyla ... 0.666667 20.0 0.42300 600.000
.. ... ... ... ... ... ... ... ... ...
79 Tree shrew Tupaia omni Scandentia ... 0.233333 15.1 0.00250 0.104
80 Bottle-nosed do... Tursiops carni Cetacea ... NaN 18.8 NaN 173.330
81 Genet Genetta carni Carnivora ... NaN 17.7 0.01750 2.000
82 Arctic fox Vulpes carni Carnivora ... NaN 11.5 0.04450 3.380
83 Red fox Vulpes carni Carnivora ... 0.350000 14.2 0.05040 4.230
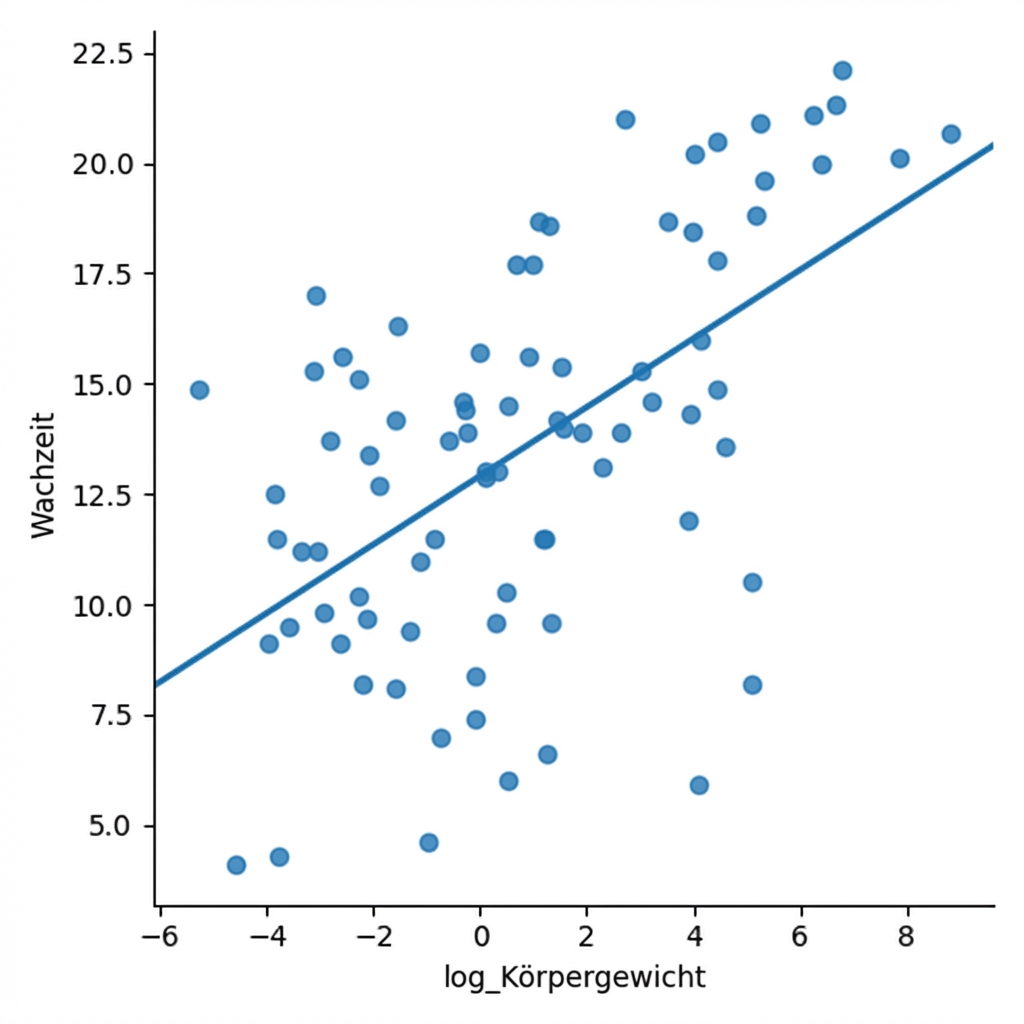
Körpergewicht vs. Wachzeit
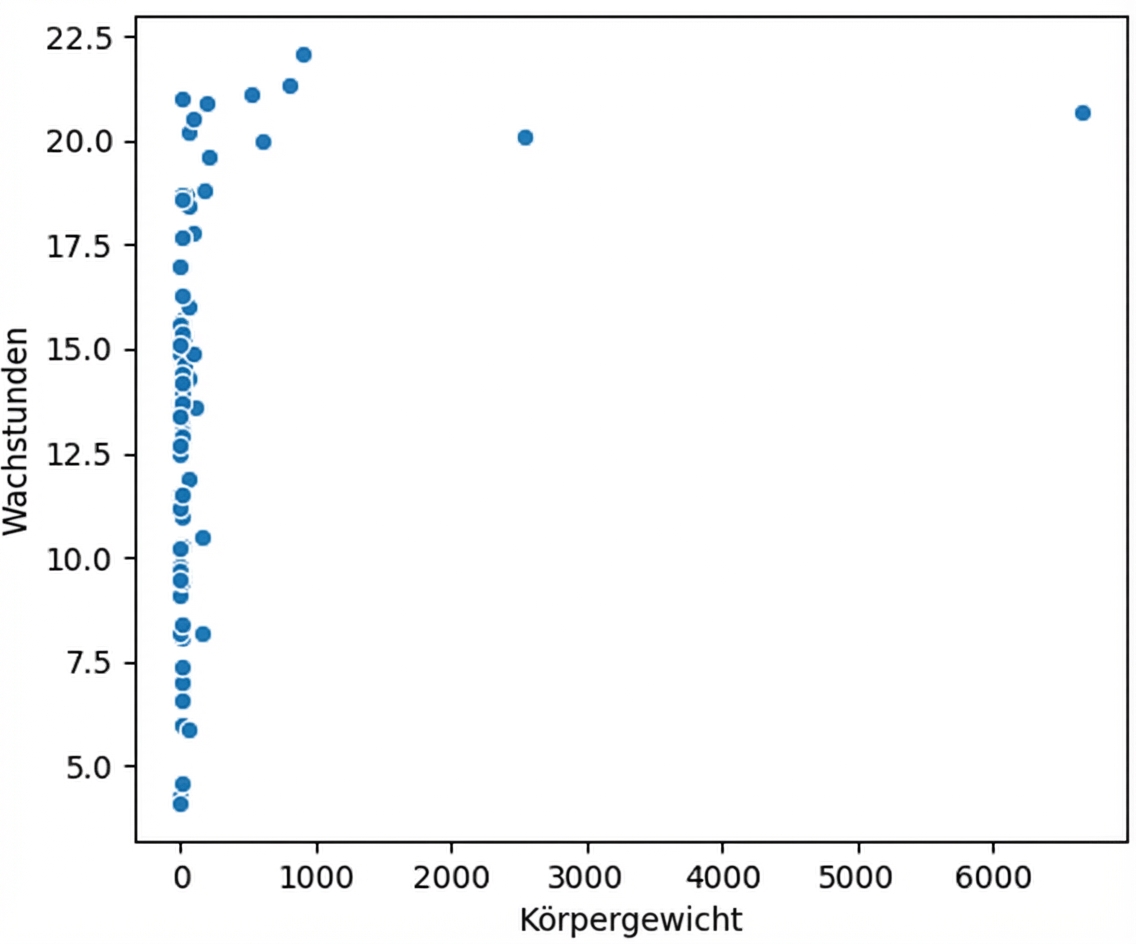
msleep['bodywt'].corr(msleep['awake'])
0.3119801
Verteilung des Körpergewichts
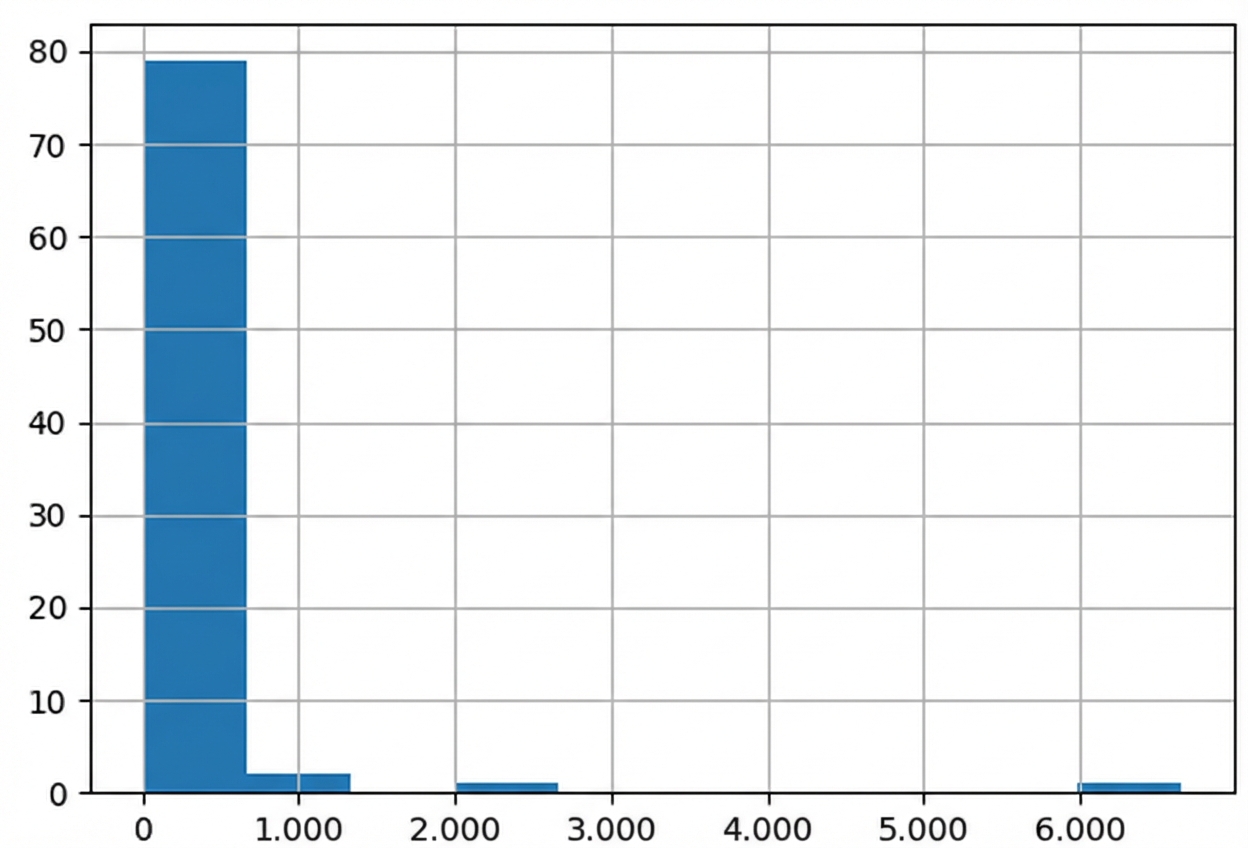
Log-Transformation
msleep['log_bodywt'] = np.log(msleep['bodywt'])sns.lmplot(x='log_bodywt', y='awake', data=msleep, ci=None) plt.show()
msleep['log_bodywt'].corr(msleep['awake'])
0.5687943
Andere Transformationen
- Log-Transformation (
log(x)) - Quadratwurzel-Transformation (
sqrt(x)) Reziproke Transformation (
1 / x)Kombinationen davon, z. B.:
log(x)undlog(y)sqrt(x)und1 / y
Warum nutzt man eine Transformation?
- Bestimmte statistische Methoden setzen voraus, dass die Variablen eine lineare Beziehung haben
- Korrelationskoeffizient
- Lineare Regression
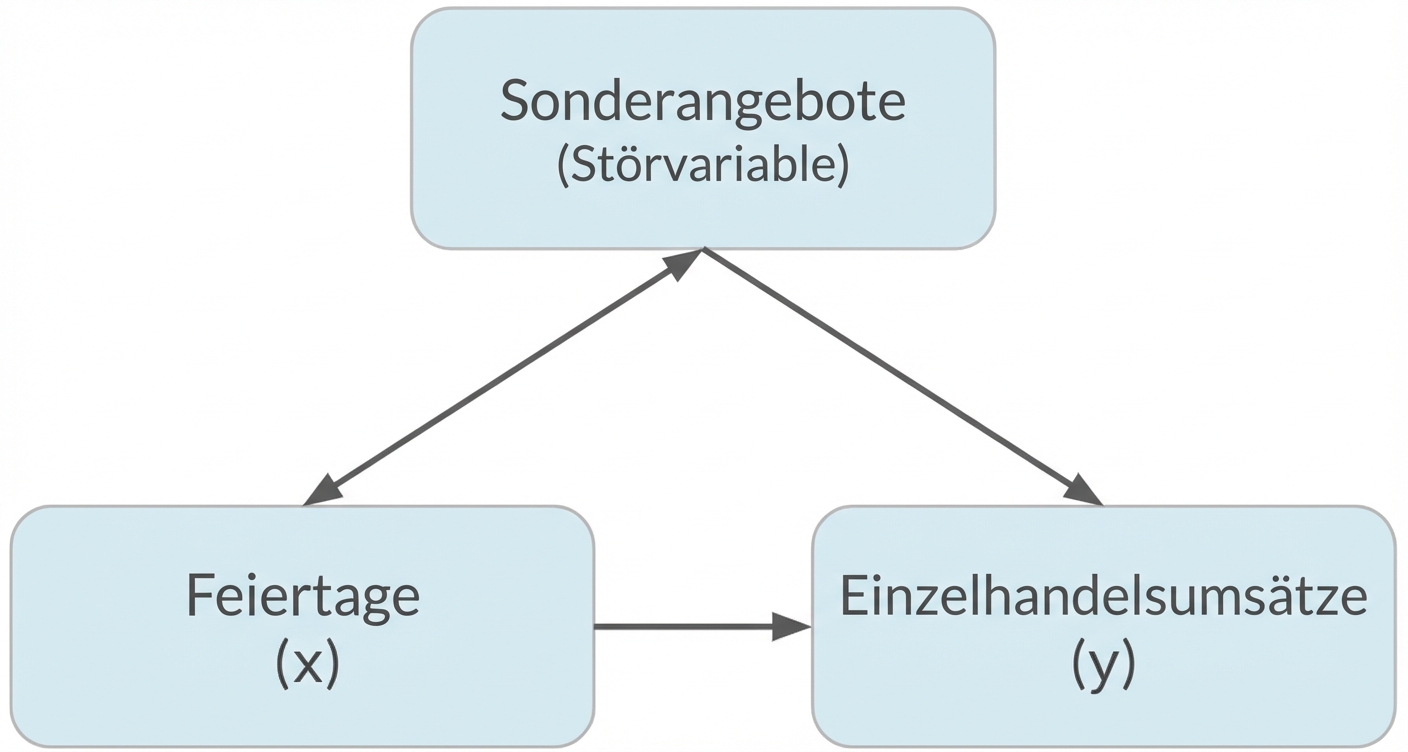
Korrelation bedeutet nicht gleich Kausalität
Wennx mit ykorreliert, bedeutet das nicht, dass x yverursacht
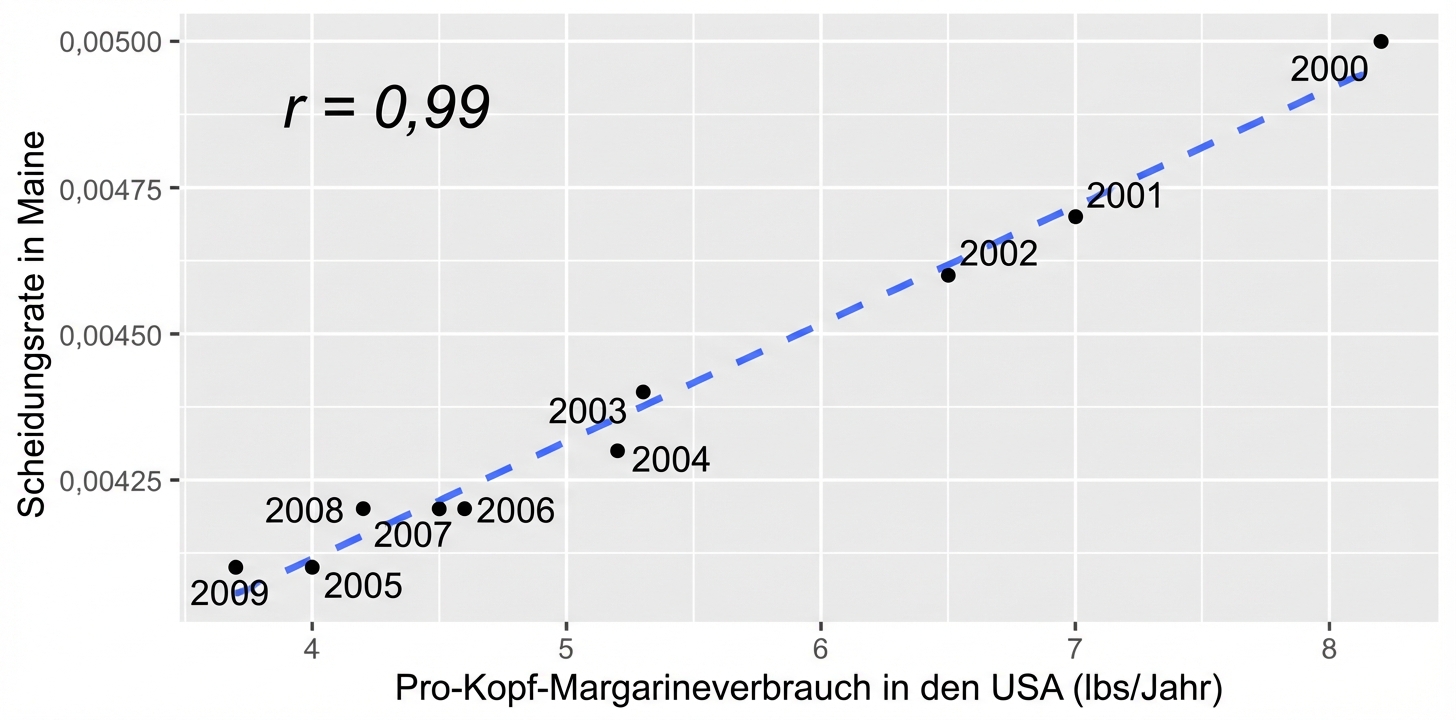
Verzerrungen
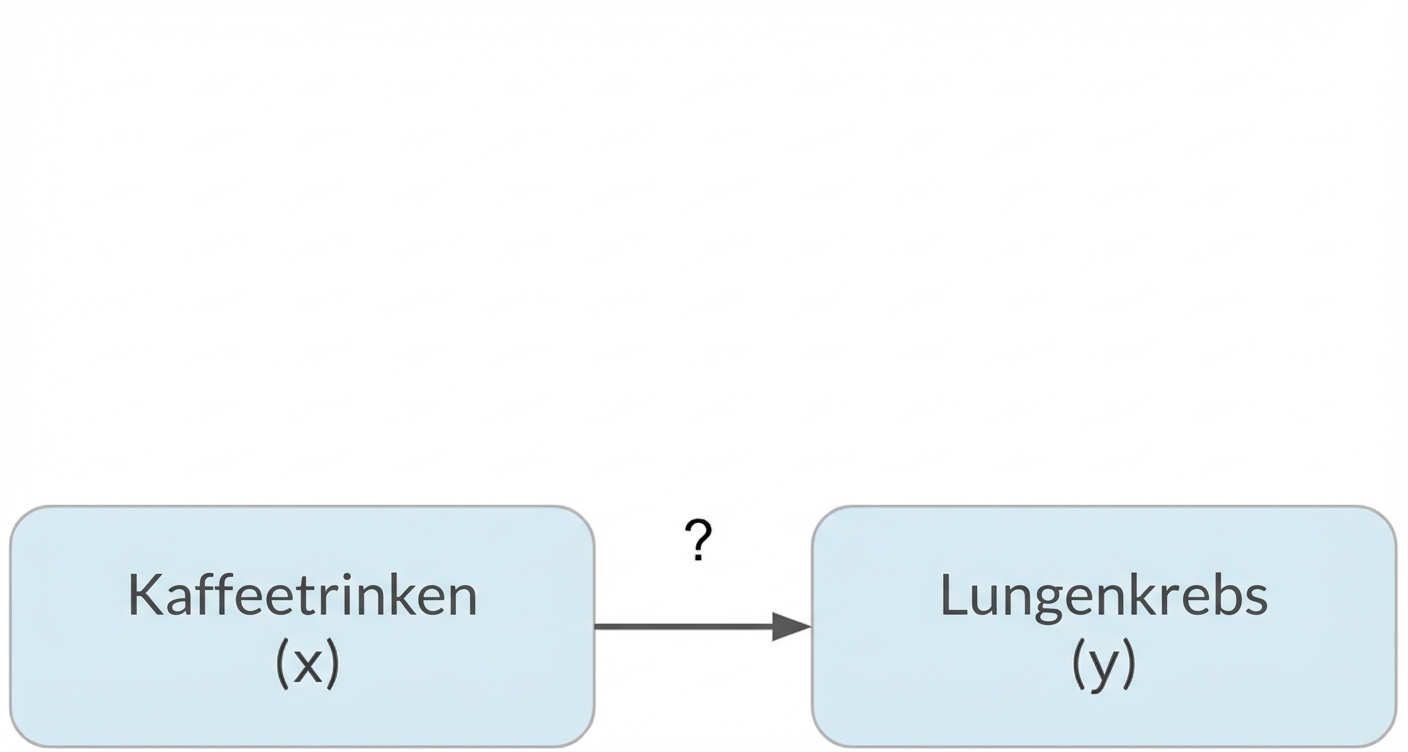
Verzerrungen
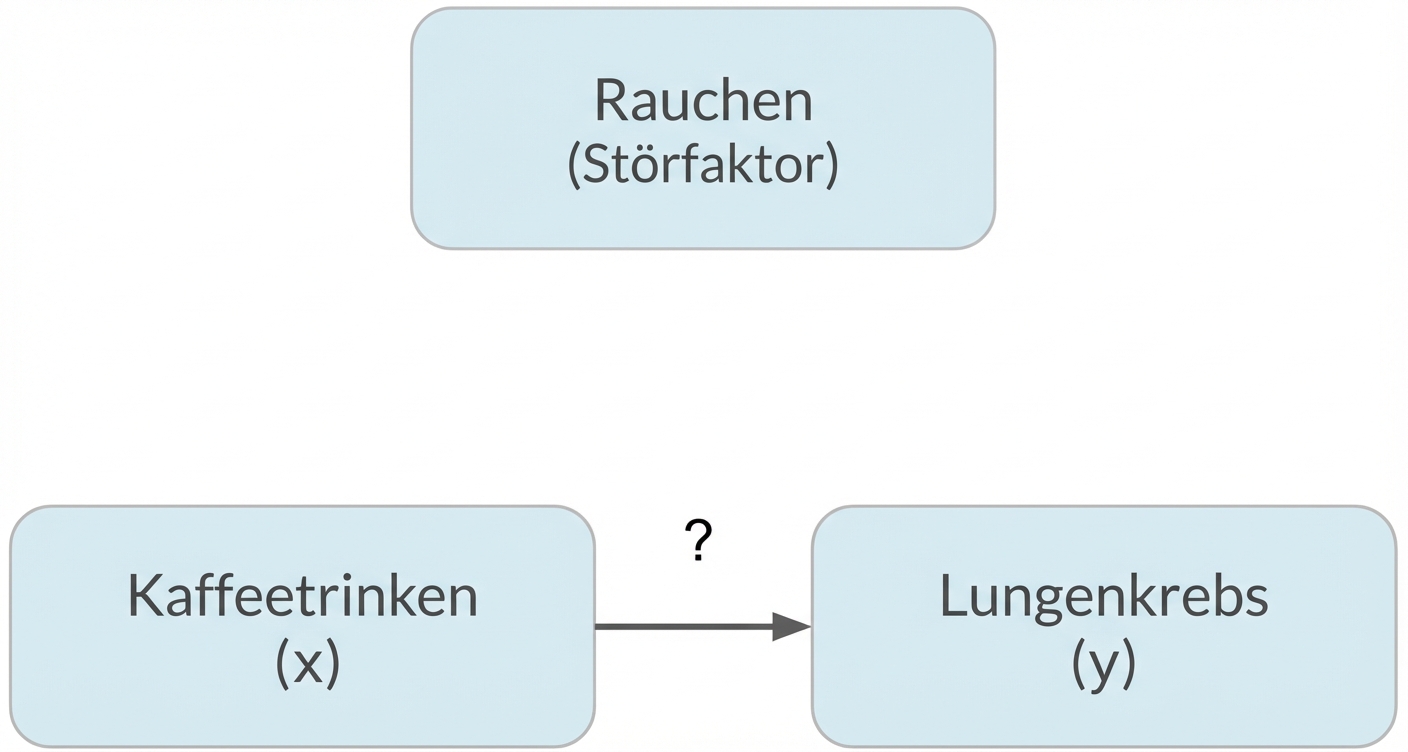
Verzerrungen
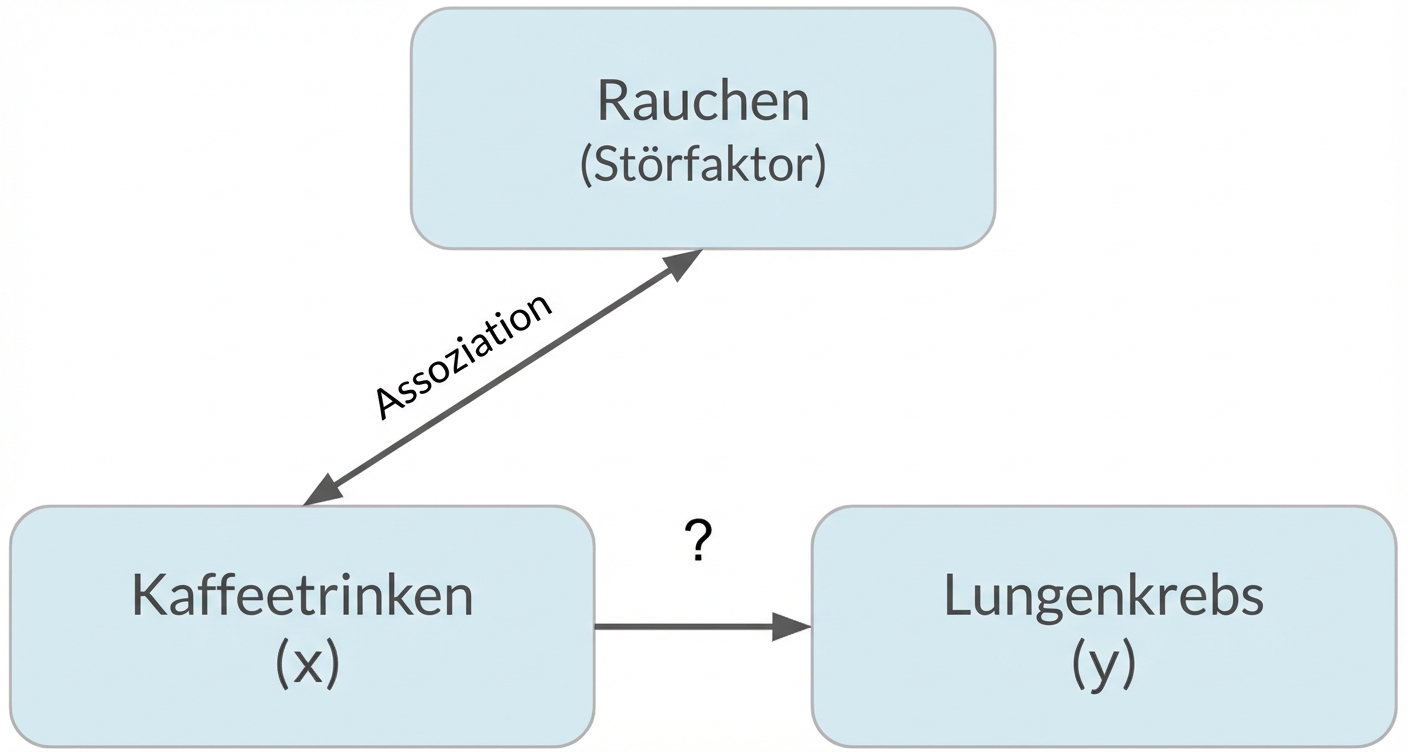
Verzerrungen
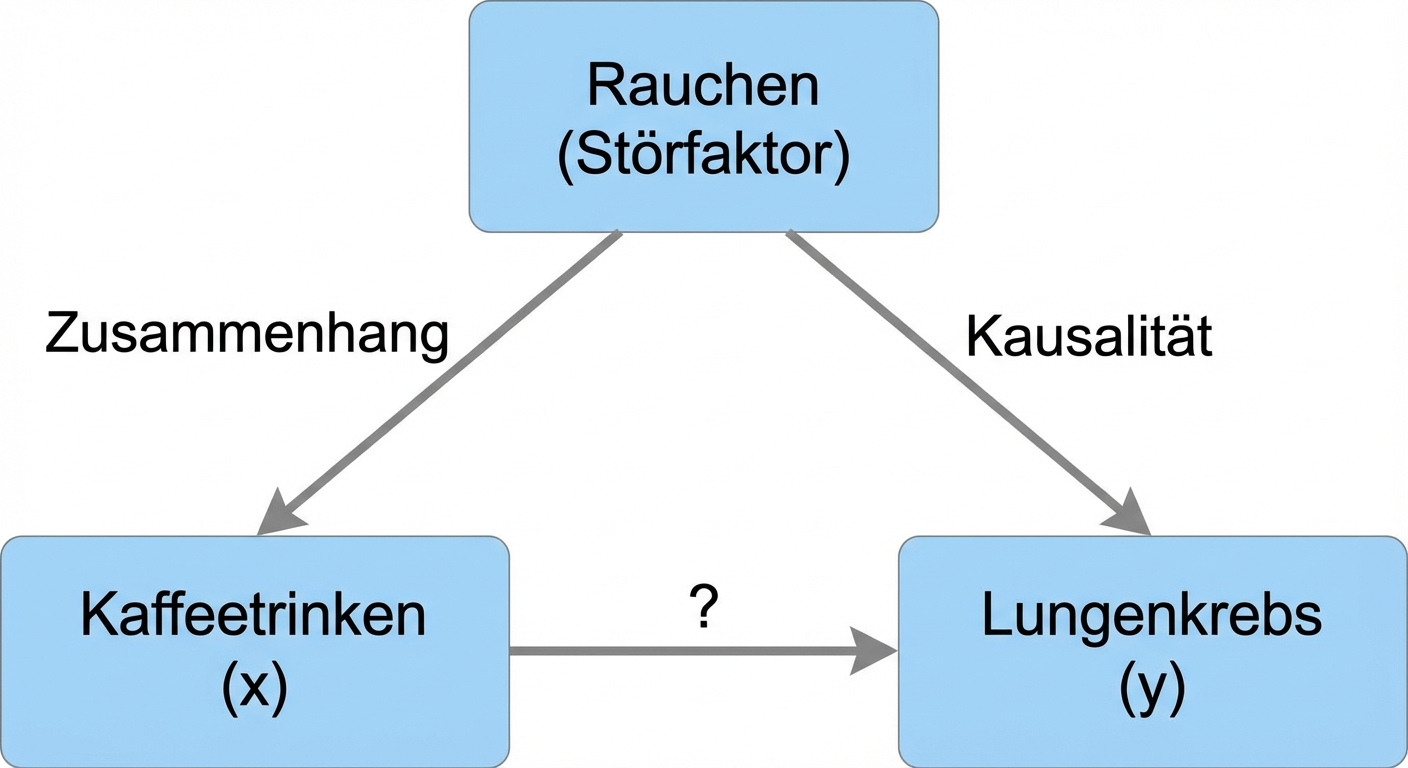
Verzerrungen
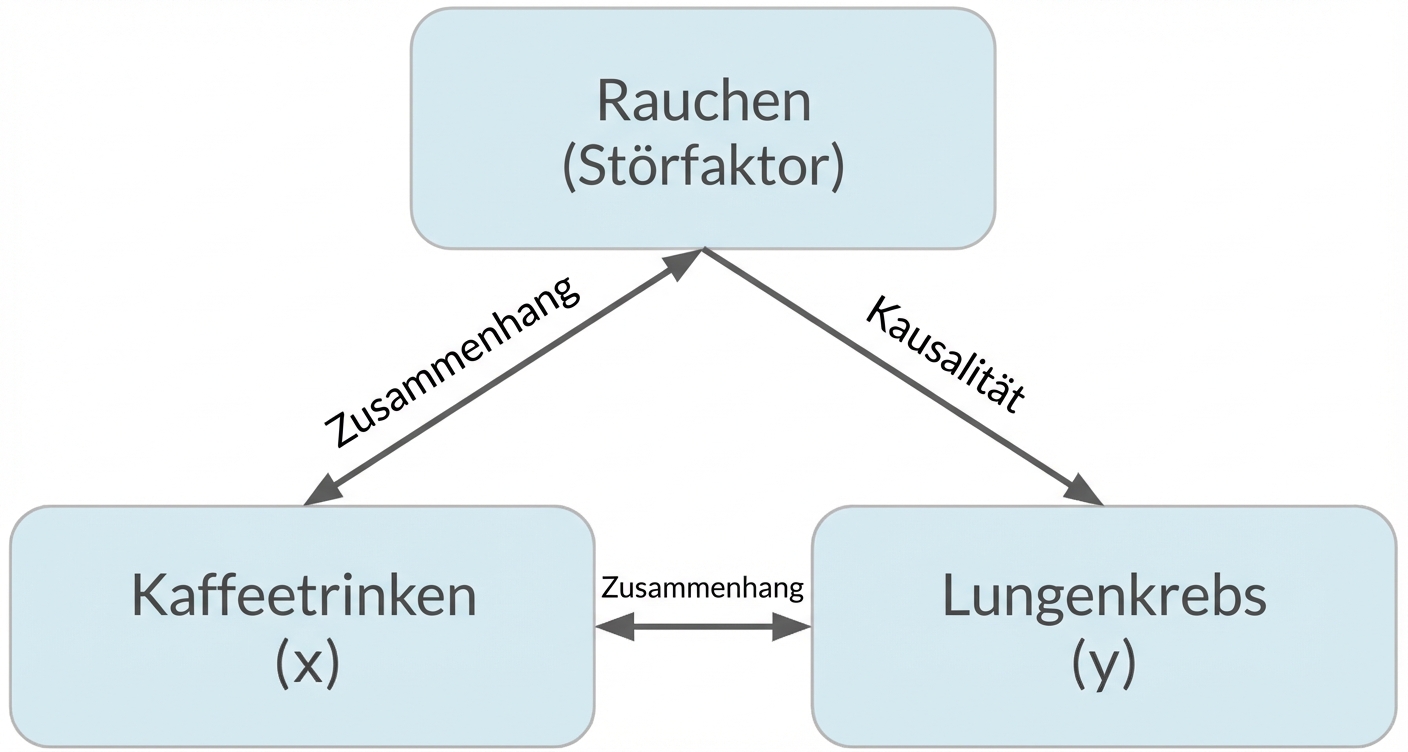
Lass uns üben!
Einführung in die Statistik in Python

