Die Binomialverteilung

Einführung in die Statistik in Python

Maggie Matsui

Content Developer, DataCamp

Der Münzwurf

Hand, die eine Münze wirft, wobei eine Seite H (Kopf) mit 50 % Wahrscheinlichkeit, die andere Seite T (Zahl) mit 50% Wahrscheinlichkeit ist

Einführung in die Statistik in Python

Binäre Ergebnisse

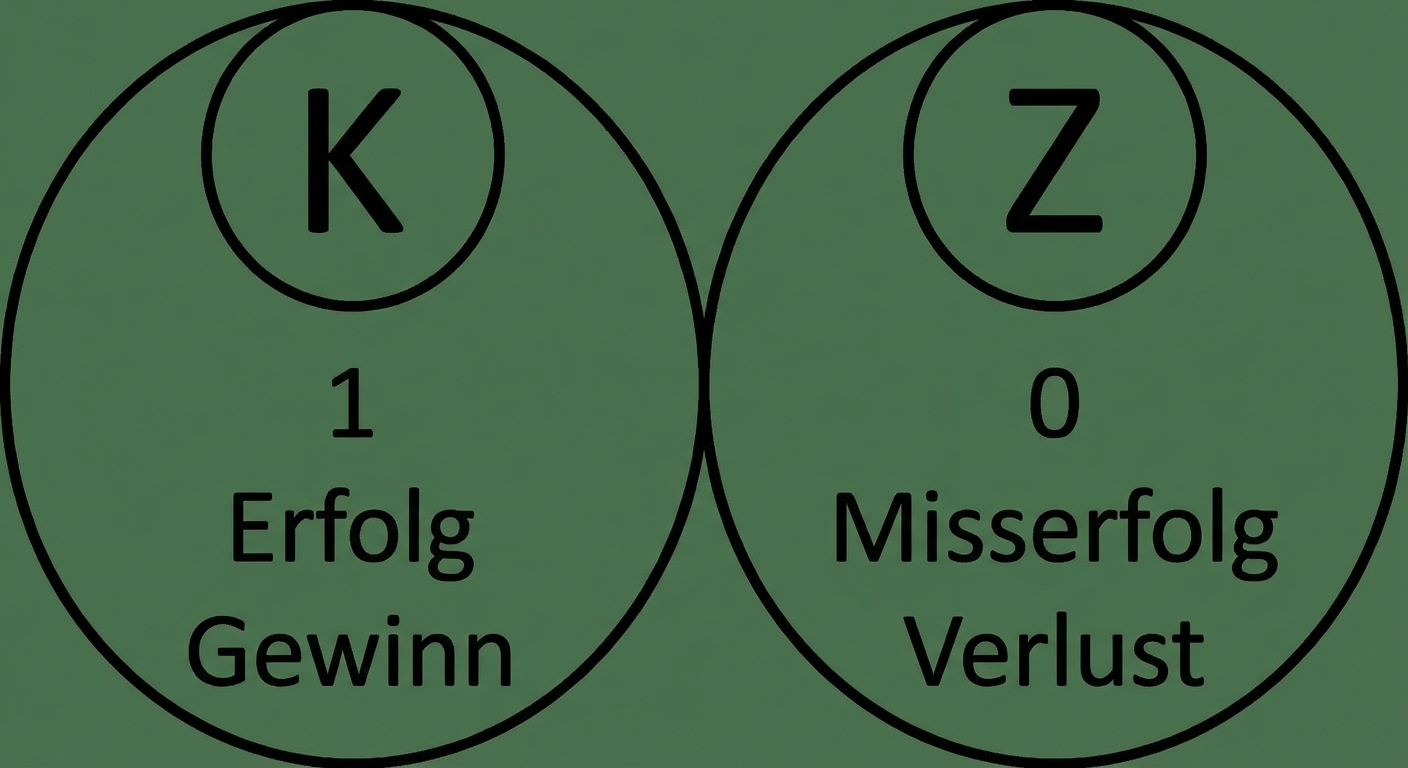
H und T, 1 und 0, Erfolg und Misserfolg, Gewinn und Verlust

Einführung in die Statistik in Python

Ein einziger Flip

binom.rvs(# of coins, probability of heads/success, size=# of trials)

1 = Kopf, 0 = Zahl

from scipy.stats import binom

binom.rvs(1, 0.5, size=1)

array([1])
Einführung in die Statistik in Python

Ein Münzwurf viele Male

binom.rvs(1, 0.5, size=8)

array([0, 1, 1, 0, 1, 0, 1, 1])

 

binom.rvs(1, 0.5, 8) mit 1 rot, 0,5 gelb, 8 blau. Text: Wirf 1 (rot) Münze mit 50 % (gelb) Erfolgschance 8 (blau) mal

Einführung in die Statistik in Python

Viele Münzwürfe ein Mal

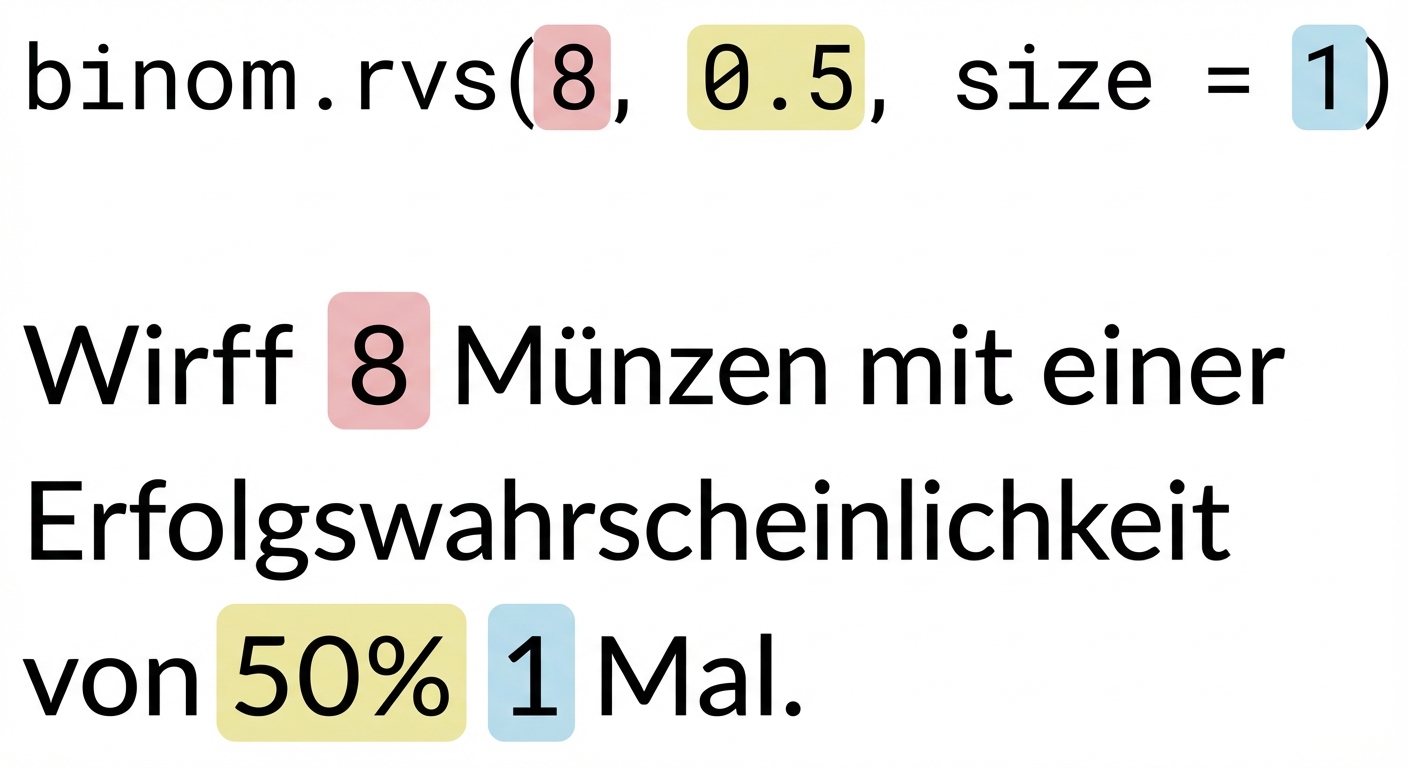
binom.rvs(8, 0.5, size=1)

array([5])

 

binom.rvs(8, 0,5, Größe = 1) mit 8 rot, 0,5 gelb, 1 blau. Text: Wirf 8 (rot) Münzen mit 50 % (gelb) Erfolgschance 1 (blau) Mal

Einführung in die Statistik in Python

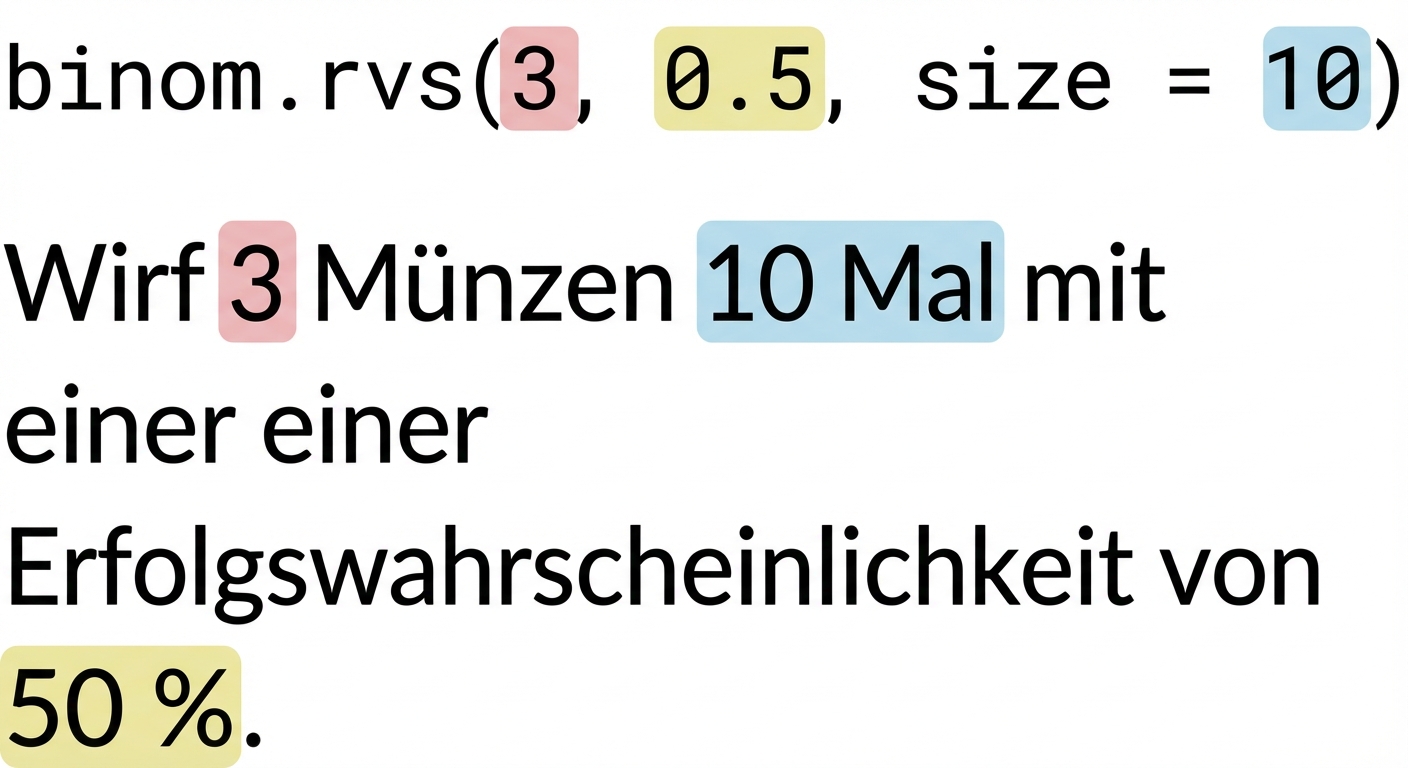
Viele Münzwürfe viele Male

binom.rvs(3, 0.5, size=10)

array([0, 3, 2, 1, 3, 0, 2, 2, 0, 0])

 

binom.rvs(3, 0.5, size=10) mit 3 rot, 0,5 gelb, 10 blau. Text: Wirf 3 Münzen (rot) mit einer Erfolgschance von 50 % (gelb) 10 (blau) mal

Einführung in die Statistik in Python

Andere Wahrscheinlichkeiten

binom.rvs(3, 0.25, size=10)

array([1, 1, 1, 1, 0, 0, 2, 0, 1, 0])

 

Bild von Münze mit Kopf mit 25%iger Wahrscheinlichkeit und mit Zahl mit 75%iger Wahrscheinlichkeit

Einführung in die Statistik in Python

Binomialverteilung

Wahrscheinlichkeitsverteilung der Anzahl von Erfolgen in einer Folge von unabhängigen Ereignissen

z. B. Anzahl der Kopfseiten in einer Folge von Münzwürfen

Beschrieben durch $n$ und $p$

  • $n$: Gesamtzahl der Versuche
  • $p$: Erfolgswahrscheinlichkeit
binom.rvs(n=10, p=0.5, size=20)

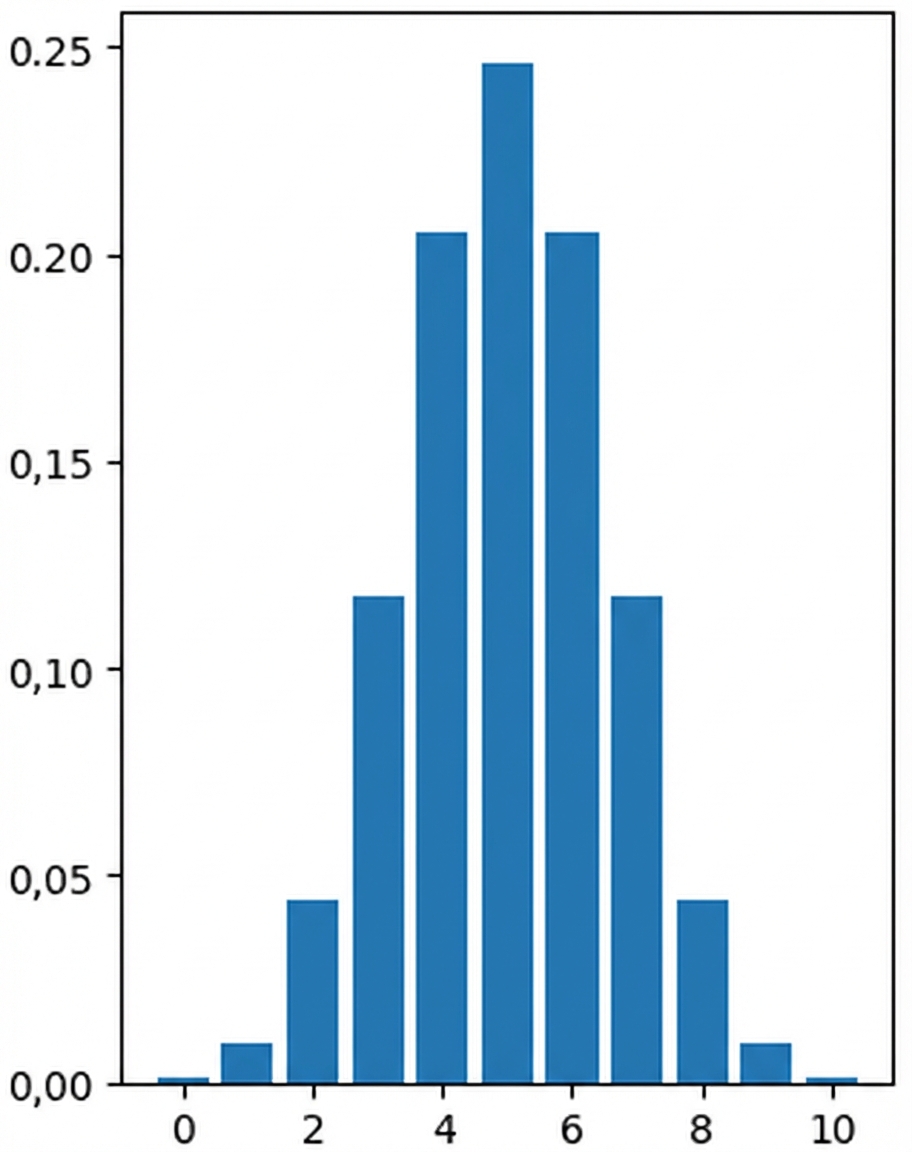
Diagramm der Binomialverteilung mit n = 10, p = 0,5

Einführung in die Statistik in Python

Wie hoch ist die Wahrscheinlichkeit für 7 Kopfseiten?

$P(\text{heads} = 7)$

# binom.pmf(num heads, num trials, prob of heads)
binom.pmf(7, 10, 0.5)

0.1171875
Einführung in die Statistik in Python

Wie hoch ist die Wahrscheinlichkeit für 7 oder weniger Mal Kopfseite?

$P(\text{heads} \le 7)$

binom.cdf(7, 10, 0.5)

0.9453125
Einführung in die Statistik in Python

Wie hoch ist die Wahrscheinlichkeit von mehr als 7 Mal Kopfseite?

$P(\text{heads} > 7)$

1 - binom.cdf(7, 10, 0.5)

0.0546875
Einführung in die Statistik in Python

Erwartungswert

$\text{Expected value} = n \times p$

Erwartete Anzahl für die Kopfseite aus 10 Würfen $= 10 \times 0,5 = 5$

Einführung in die Statistik in Python

Unabhängigkeit

Die Binomialverteilung beschreibt die Anzahl der Erfolge bei unabhängigen Versuchen

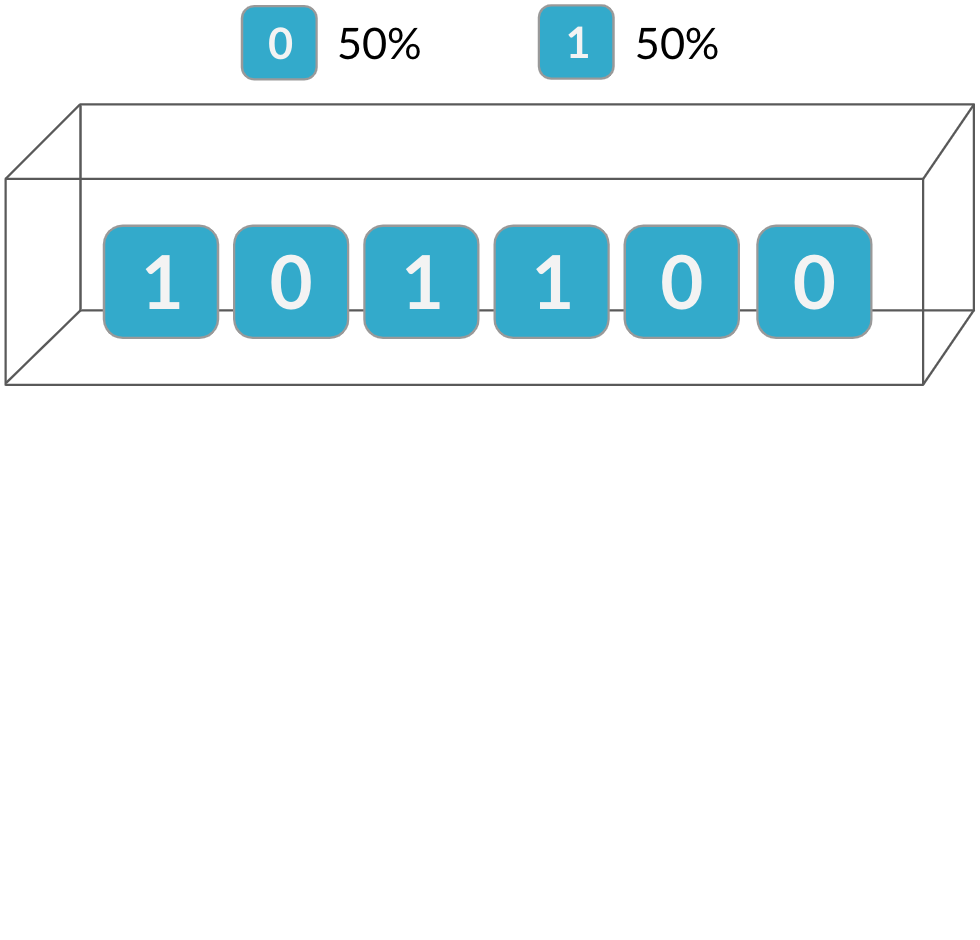
Box mit Tickets mit 3 Nullen und 3 Einsen. 50 % Wahrscheinlichkeit für 0, 50 % Wahrscheinlichkeit für 1

Einführung in die Statistik in Python

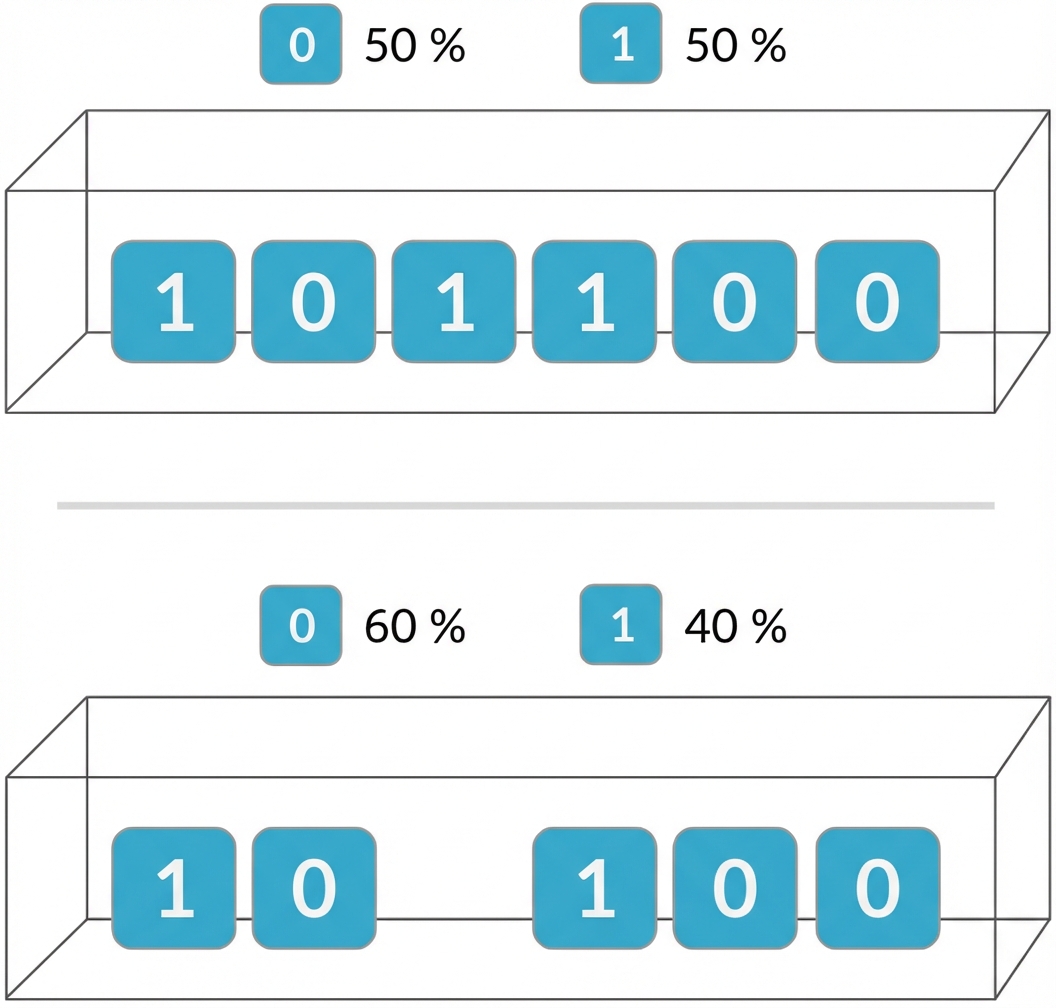
Unabhängigkeit

Die Binomialverteilung beschreibt die Anzahl der Erfolge bei unabhängigen Versuchen

 

Die Wahrscheinlichkeiten des zweiten Versuchs verändern sich aufgrund des Ergebnisses des ersten Versuchs

 

Wenn die Versuche nicht unabhängig sind, gilt die Binomialverteilung nicht!

Box mit Tickets mit 3 Nullen und 2 Einsen. 60 % Wahrscheinlichkeit für 0, 40 % Wahrscheinlichkeit für 1

Einführung in die Statistik in Python

Lass uns üben!

Einführung in die Statistik in Python

Preparing Video For Download...