Maße der Streuung

Einführung in die Statistik in Python

Maggie Matsui

Content Developer, DataCamp

Was ist Streuung?

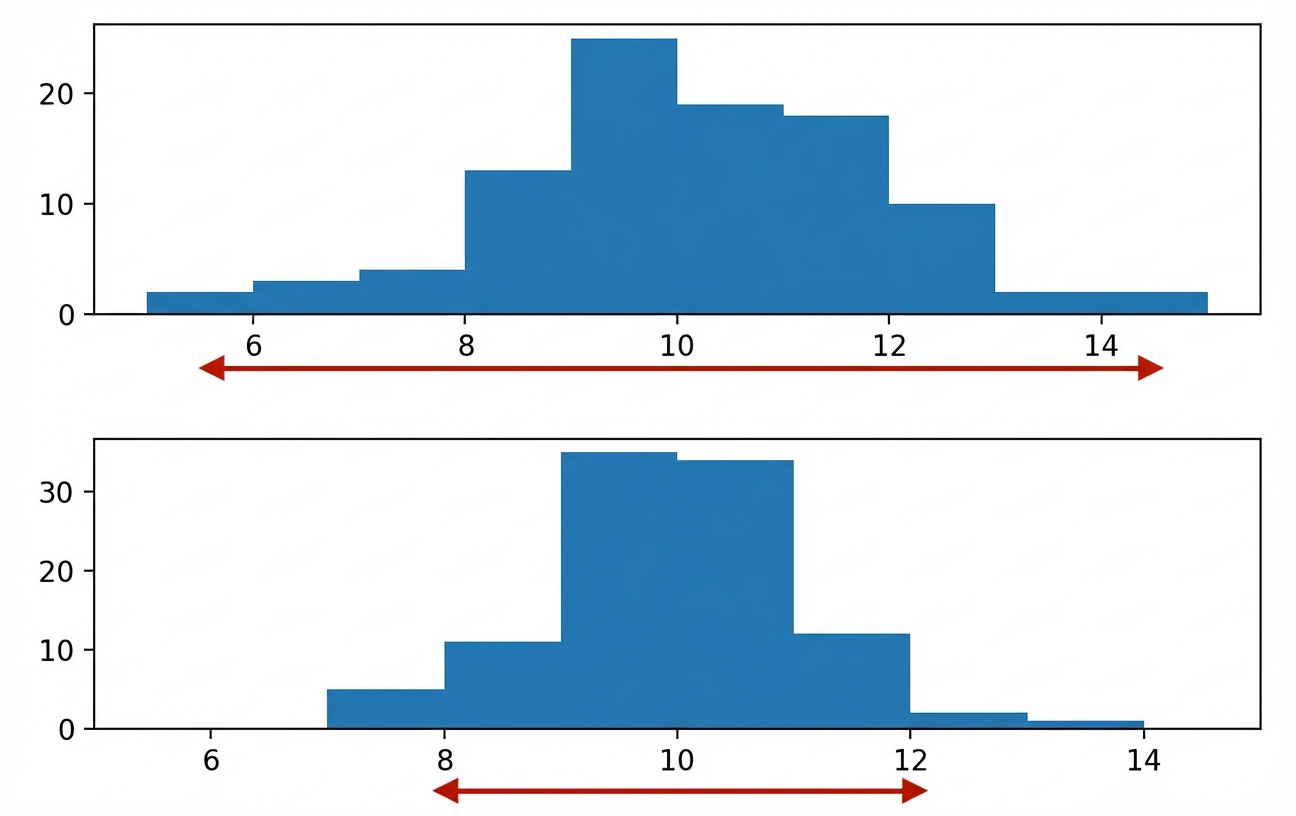
Zwei Histogramme: ein schmales mit Daten, die nur wenige Werte umfassen, und ein breiteres mit Daten, die mehr Werte umfassen

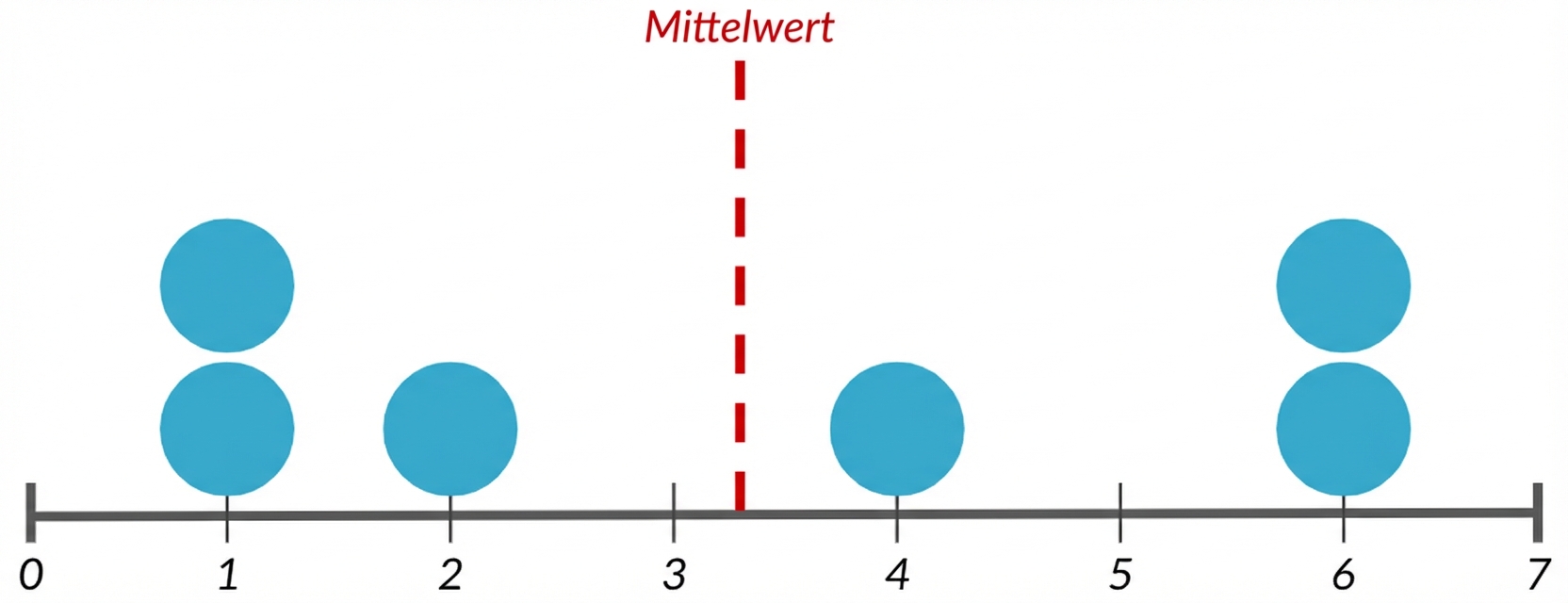
Varianz

Durchschnittliche Distanz von jedem Datenpunkt zum Mittelwert der Daten

Ein Punktdiagramm mit 7 Datenpunkten und einer roten Linie in der Mitte, die den Mittelwert darstellt

Varianz

Durchschnittliche Distanz von jedem Datenpunkt zum Mittelwert der Daten

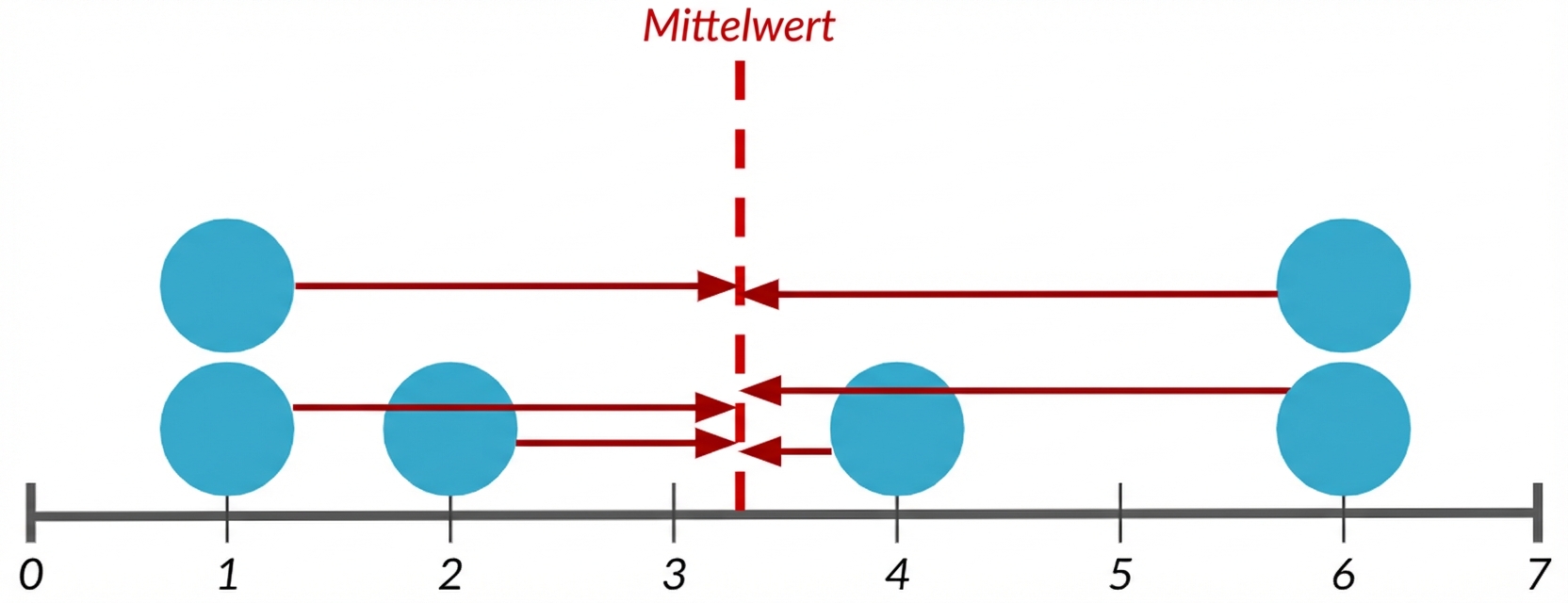
Ein Punktdiagramm mit 7 Datenpunkten und einer roten Linie in der Mitte als Mittelwert. Zwischen jedem Punkt und dem Mittelwert sind Pfeile eingezeichnet.

Berechnung der Varianz

1. Den Mittelwert von jedem Datenpunkt subtrahieren

dists = msleep['sleep_total'] - 
        np.mean(msleep['sleep_total'])
print(dists)

0     1.666265
1     6.566265
2     3.966265
3     4.466265
4    -6.433735
      ...

2. Jede Entfernung quadrieren

sq_dists = dists ** 2
print(sq_dists)

0      2.776439
1     43.115837
2     15.731259
3     19.947524
4     41.392945
      ...

Berechnung der Varianz

3. Summe der quadrierten Distanzen

sum_sq_dists = np.sum(sq_dists)
print(sum_sq_dists)

1624.065542

4. Durch die Anzahl der Datenpunkte dividieren - 1

variance = sum_sq_dists / (83 - 1)
print(variance)

19.805677

np.var(){{4}}verwenden

np.var(msleep['sleep_total'], ddof=1)

19.805677

Ohne ddof=1 wird die Varianz der Grundgesamtheit statt der Varianz der Stichprobe berechnet:

np.var(msleep['sleep_total'])

19.567055

Standardabweichung

np.sqrt(np.var(msleep['sleep_total'], ddof=1))

4.450357

np.std(msleep['sleep_total'], ddof=1)

4.450357

Mittlere absolute Abweichung

dists = msleep['sleep_total'] - np.mean(msleep['sleep_total'])

np.mean(np.abs(dists))

3.566701

Standardabweichung vs. mittlere absolute Abweichung

Die Standardabweichung quadriert die Distanzen, wobei längere Distanzen stärker bestraft werden als kürzere.
Bei der mittleren absoluten Abweichung wird jede Distanz gleich bestraft.
Das eine ist nicht besser als das andere, aber die Standardabweichung kommt häufiger vor als die mittlere absolute Abweichung.

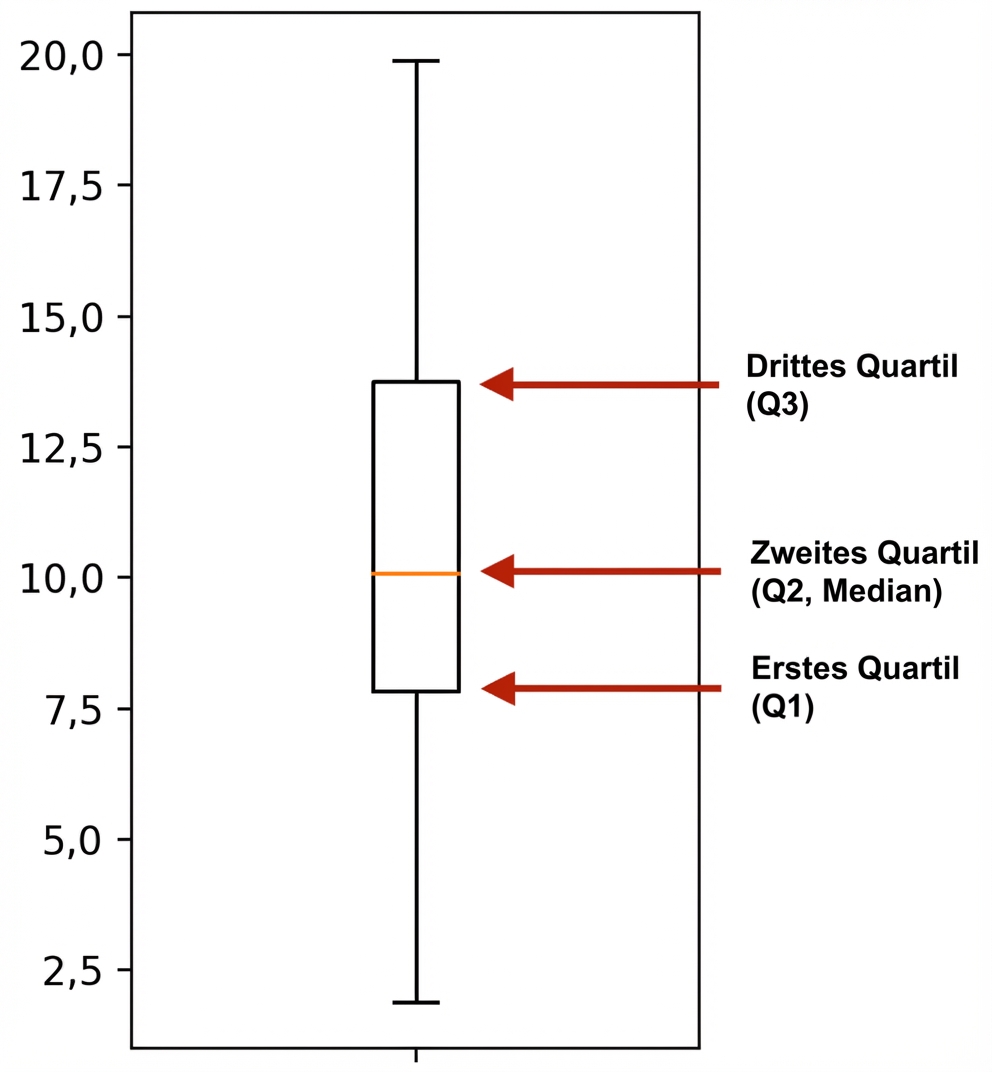
Quantilen

np.quantile(msleep['sleep_total'], 0.5)

10.1

0,5 Quantil = Median

Quartile:

np.quantile(msleep['sleep_total'], [0, 0.25, 0.5, 0.75, 1])

array([ 1.9 ,  7.85, 10.1 , 13.75, 19.9 ])

Kastendiagramme verwenden Quartile

import matplotlib.pyplot as plt
plt.boxplot(msleep['sleep_total'])
plt.show()

sleep_total boxplot.png

Quantilen mit np.linspace()

np.quantile(msleep['sleep_total'], [0, 0.2, 0.4, 0.6, 0.8, 1])

array([ 1.9 ,  6.24,  9.48, 11.14, 14.4 , 19.9 ])

np.linspace(start, stop, num)

np.quantile(msleep['sleep_total'], np.linspace(0, 1, 5))

array([ 1.9 ,  7.85, 10.1 , 13.75, 19.9 ])

Interquartilsabstand (IQR)

Höhe des Kastens in einem Kastendiagramm

np.quantile(msleep['sleep_total'], 0.75) - np.quantile(msleep['sleep_total'], 0.25)

5.9

from scipy.stats import iqr
iqr(msleep['sleep_total'])

5.9

Ausreißer

Ausreißer: Datenpunkt, der sich erheblich von den anderen unterscheidet

Woher wissen wir, was ein wesentlicher Unterschied ist? Ein Datenpunkt ist ein Ausreißer, wenn:

$\text{data} < \text{Q1} - 1.5\times\text{IQR}$ oder
$\text{Daten} > \text{Q3} + 1,5\times\text{IQR}$

Ausreißer finden

from scipy.stats import iqr
iqr = iqr(msleep['bodywt'])

lower_threshold = np.quantile(msleep['bodywt'], 0.25) - 1.5 * iqr
upper_threshold = np.quantile(msleep['bodywt'], 0.75) + 1.5 * iqr

msleep[(msleep['bodywt'] < lower_threshold) | (msleep['bodywt'] > upper_threshold)]

                    name   vore  sleep_total    bodywt
4                    Cow  herbi          4.0   600.000
20        Asian elephant  herbi          3.9  2547.000
22                 Horse  herbi          2.9   521.000
...

Alles in einem Rutsch

msleep['bodywt'].describe()

count      83.000000
mean      166.136349
std       786.839732
min         0.005000
25%         0.174000
50%         1.670000
75%        41.750000
max      6654.000000
Name: bodywt, dtype: float64

Lass uns üben!

Einführung in die Statistik in Python