Diskrete Verteilungen
Einführung in die Statistik in Python

Maggie Matsui
Content Developer, DataCamp
Würfeln

Würfeln

Vertriebspersonal auswählen
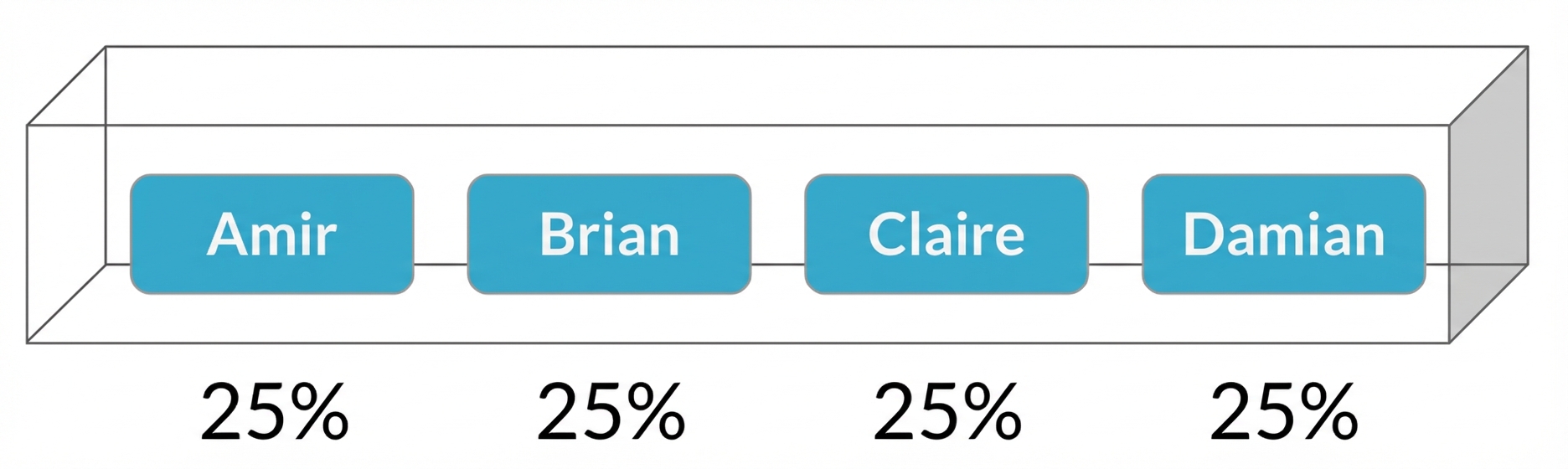
Wahrscheinlichkeitsverteilung
Beschreibt die Wahrscheinlichkeit eines jeden möglichen Ergebnisses in einem Szenario
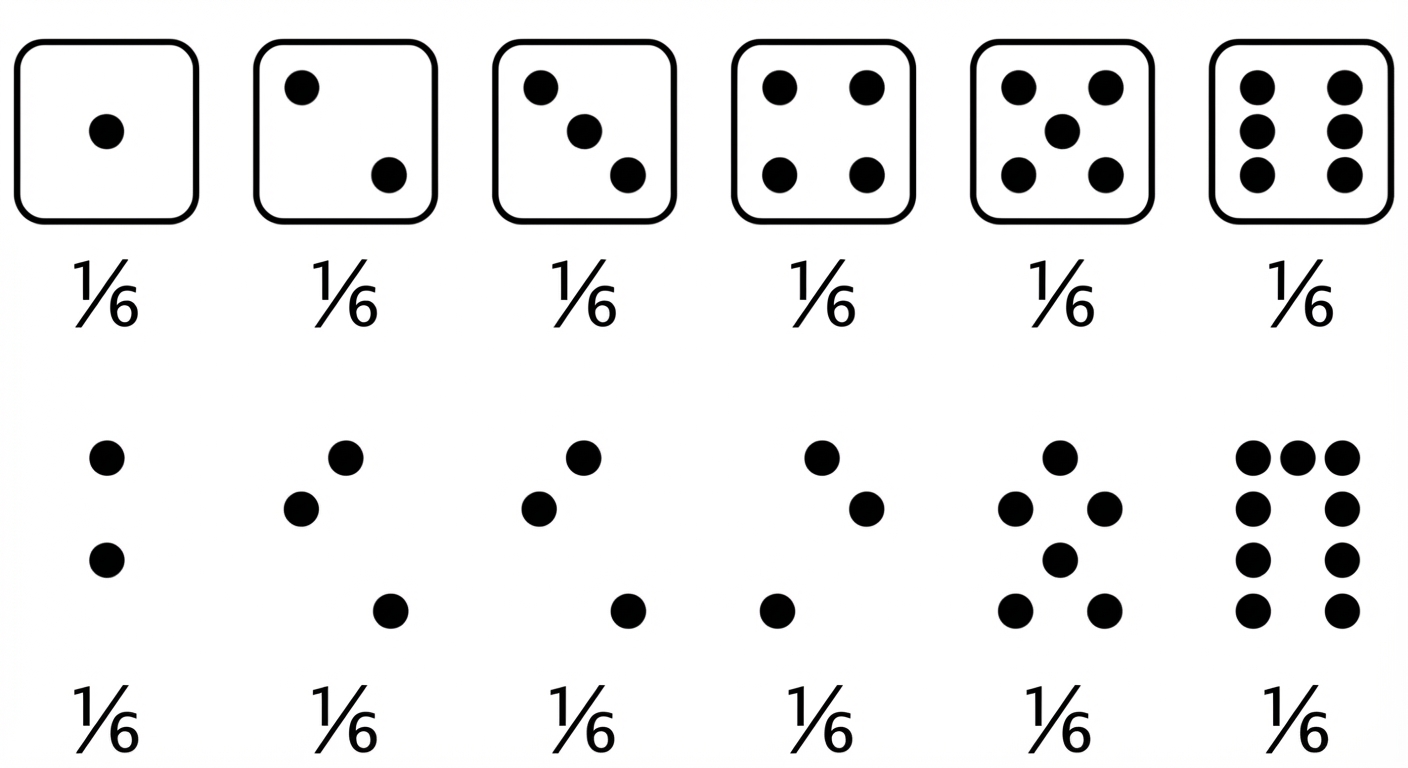
Erwartungswert: Mittelwert einer Wahrscheinlichkeitsverteilung
Erwarteter Wert eines Wurfs eines gleichseitigen Würfels = $(1 \times \frac{1}{6}) + (2 \times \frac{1}{6}) +(3 \times \frac{1}{6}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3,5$
Visualisierung einer Wahrscheinlichkeitsverteilung
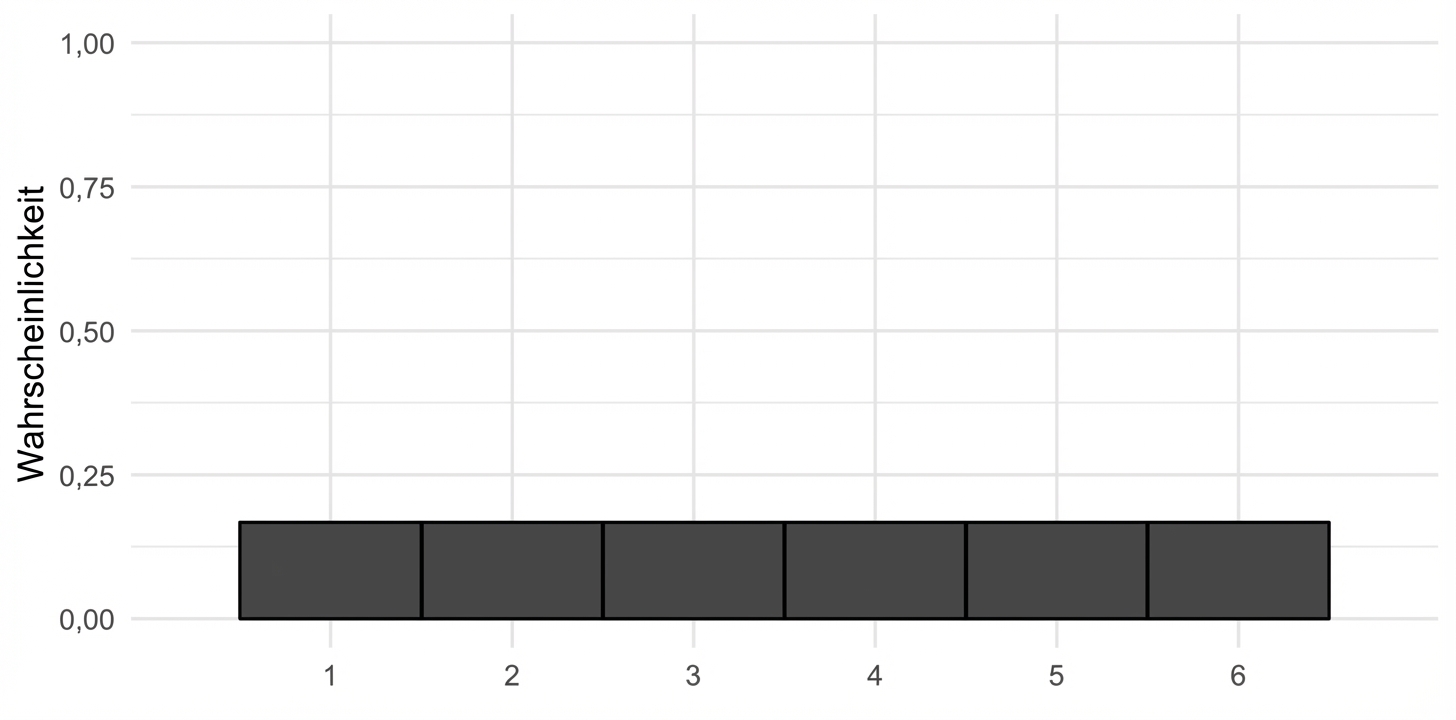
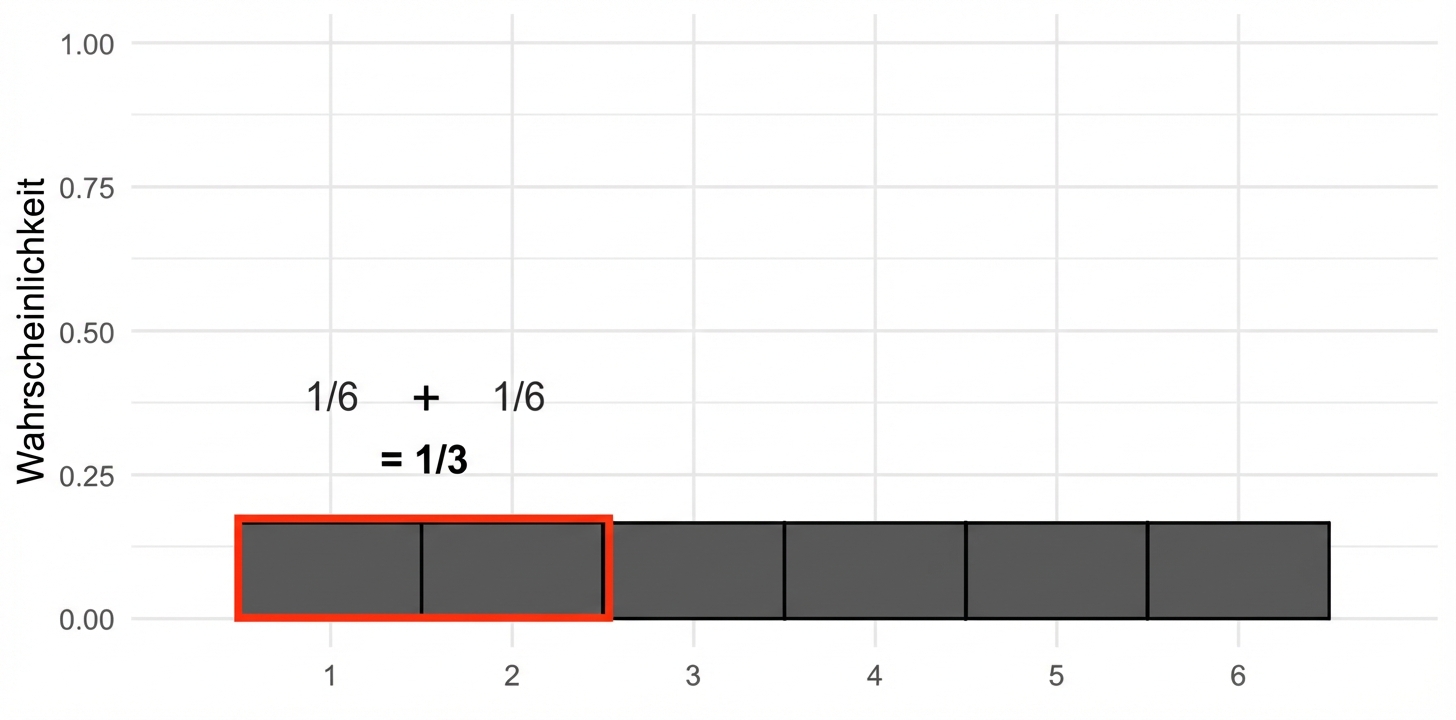
Wahrscheinlichkeit = Fläche
$$P(\text{die roll}) \le 2 = ~?$$
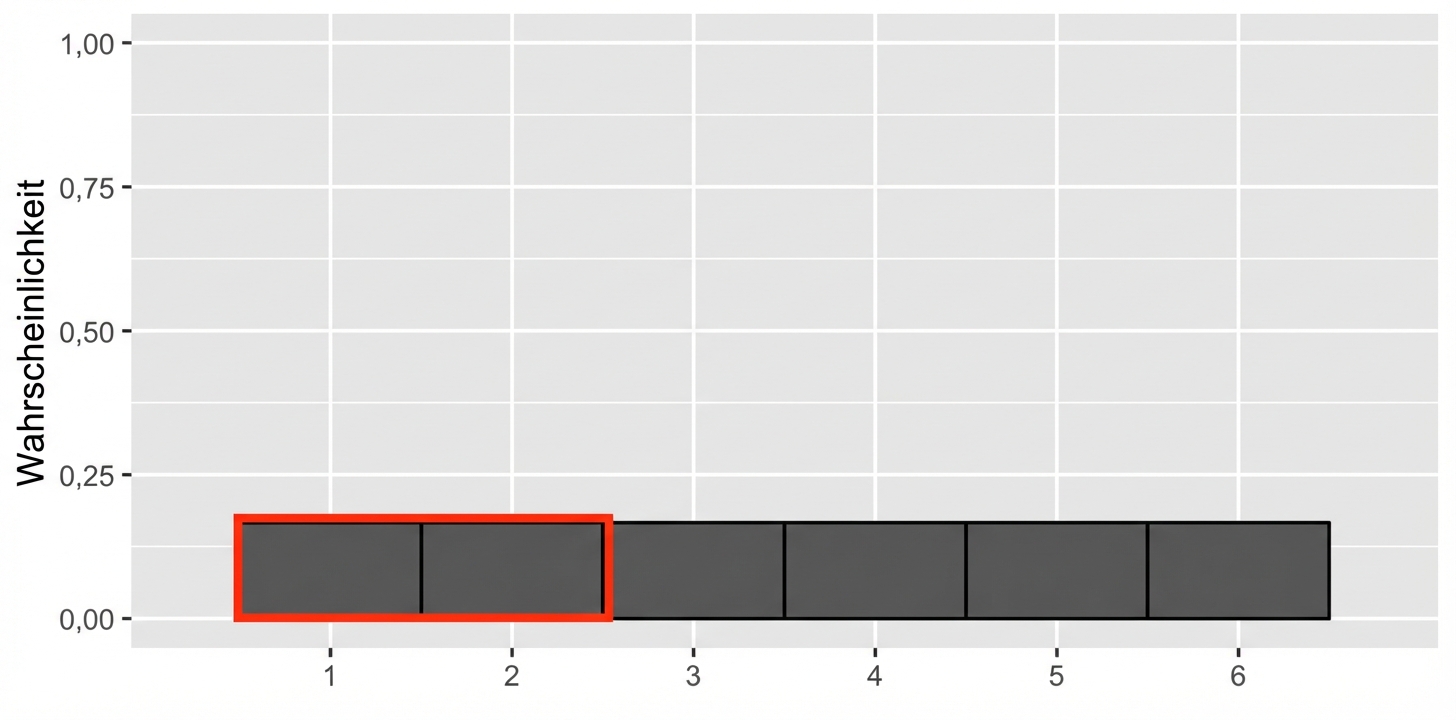
Wahrscheinlichkeit = Fläche
$$P(\text{die roll}) \le 2 = 1/3$$
Ungerader Würfel
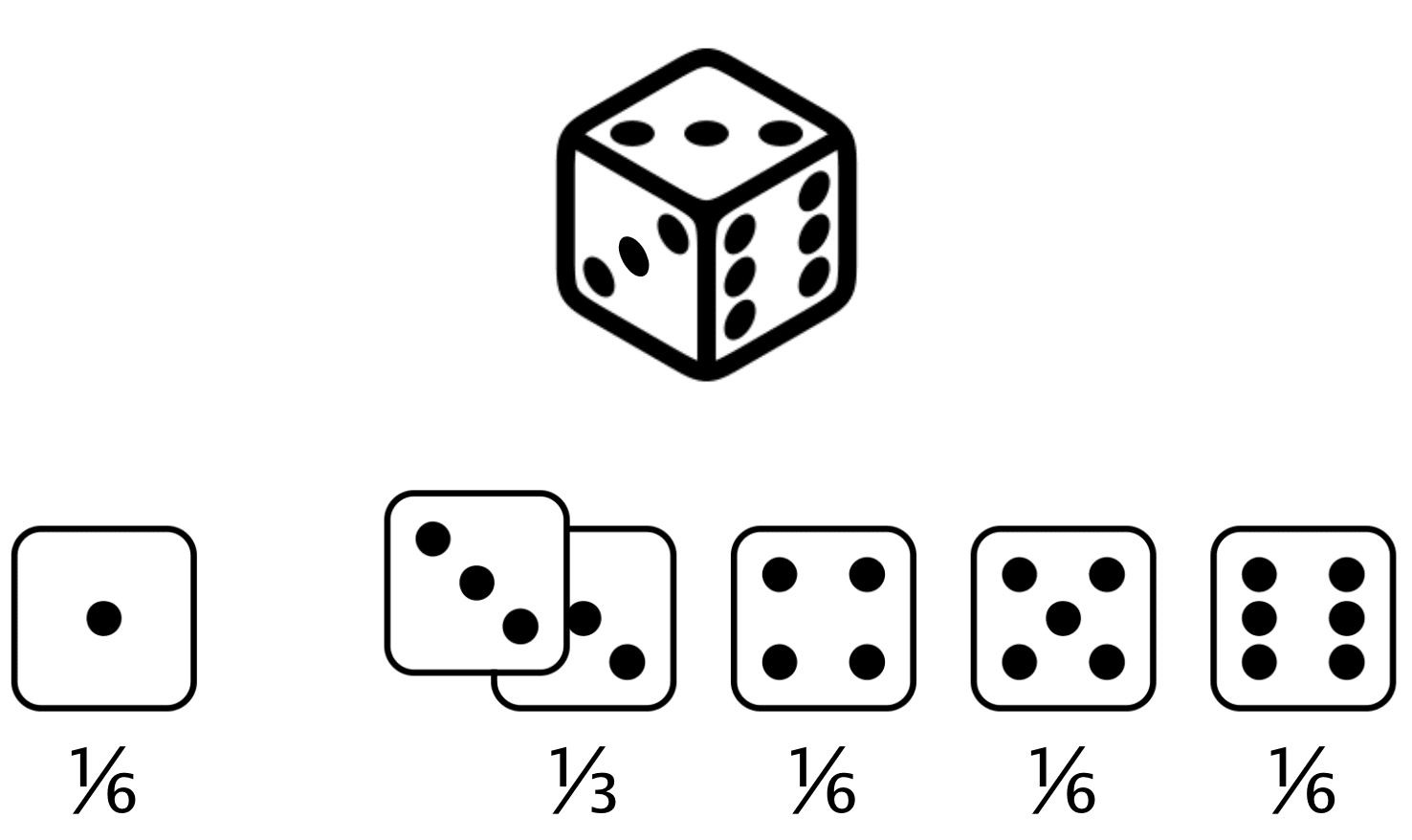
Erwarteter Wert eines ungeraden Würfelwurfs = $(1 \times \frac{1}{6}) +(2 \times 0) +(3 \times \frac{1}{3}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3,67 $
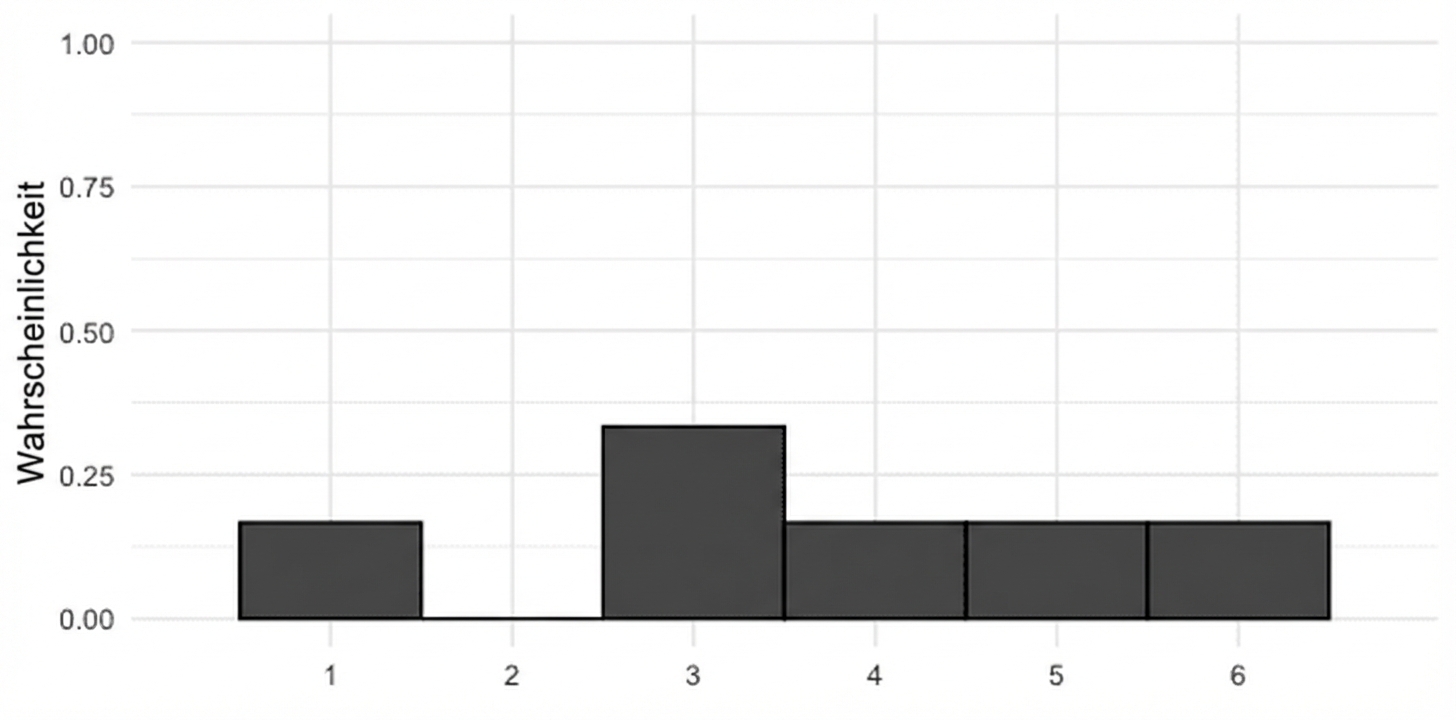
Visualisieren ungleichverteilter Wahrscheinlichkeiten
Addieren von Flächen
$$P(\text{uneven die roll}) \le 2 = ~?$$
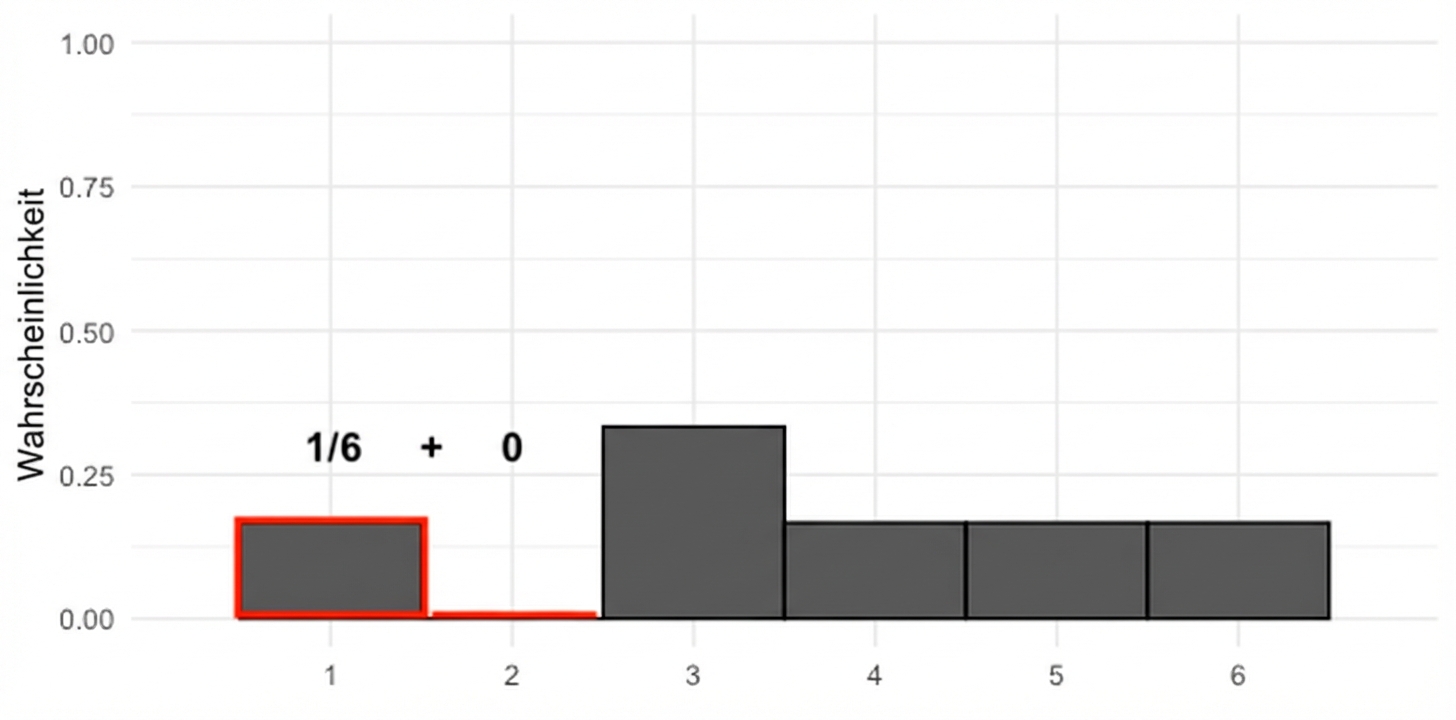
Addieren von Flächen
$$P(\text{uneven die roll}) \le 2 = 1/6$$

Diskrete Wahrscheinlichkeitsverteilungen
Beschreibe Wahrscheinlichkeiten für diskrete Ergebnisse
Gleichseitiger Würfel

Diskrete Gleichverteilung
Ungerader Würfel

Stichproben aus diskreten Verteilungen
print(die)
number prob
0 1 0.166667
1 2 0.166667
2 3 0.166667
3 4 0.166667
4 5 0.166667
5 6 0.166667
np.mean(die['number'])
3.5
rolls_10 = die.sample(10, replace = True)
rolls_10
number prob
0 1 0.166667
0 1 0.166667
4 5 0.166667
1 2 0.166667
0 1 0.166667
0 1 0.166667
5 6 0.166667
5 6 0.166667
...
Visualisieren einer Stichprobe
rolls_10['number'].hist(bins=np.linspace(1,7,7))
plt.show()
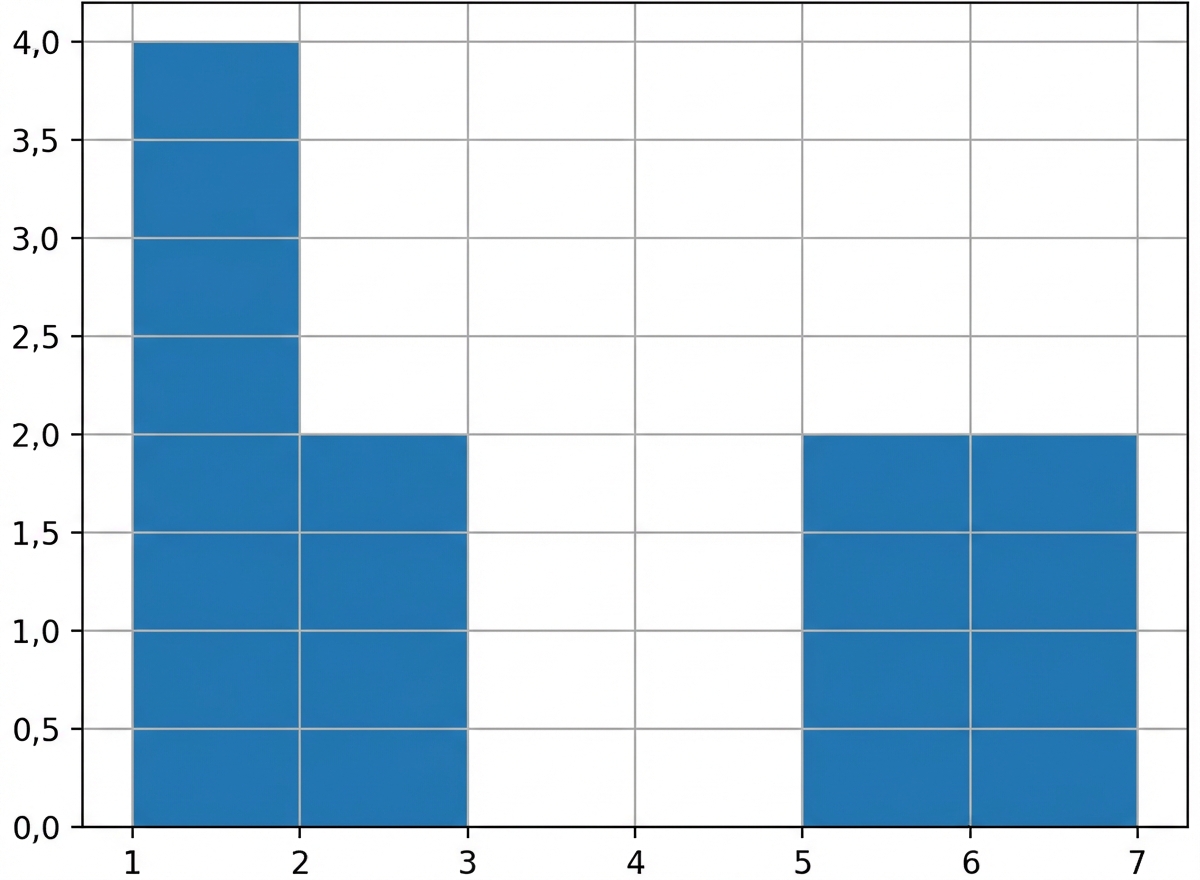
Stichprobenverteilung vs. theoretische Verteilung
Stichprobe mit 10 Würfen

np.mean(rolls_10['number']) = 3.0
Theoretische Wahrscheinlichkeitsverteilung
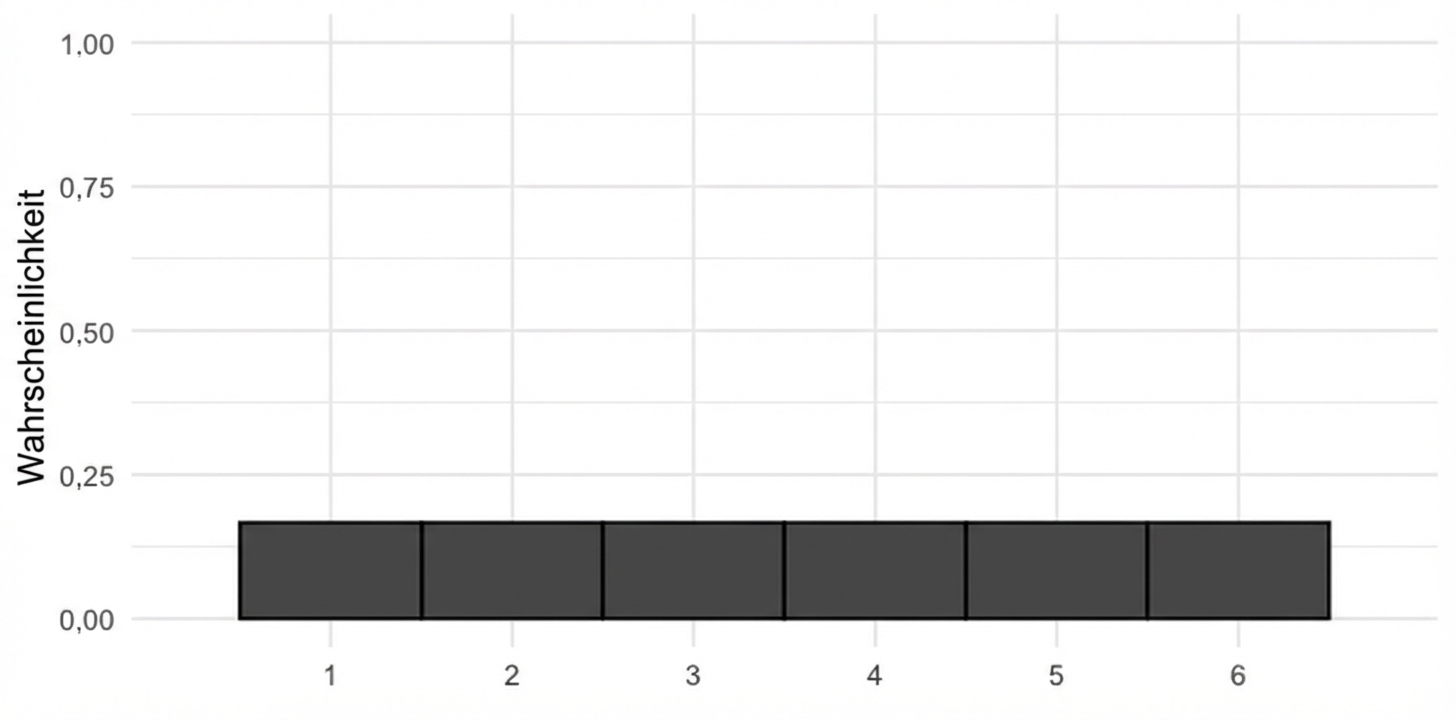
mean(die['number']) = 3.5
Eine größere Stichprobe
Stichprobe mit 100 Würfen
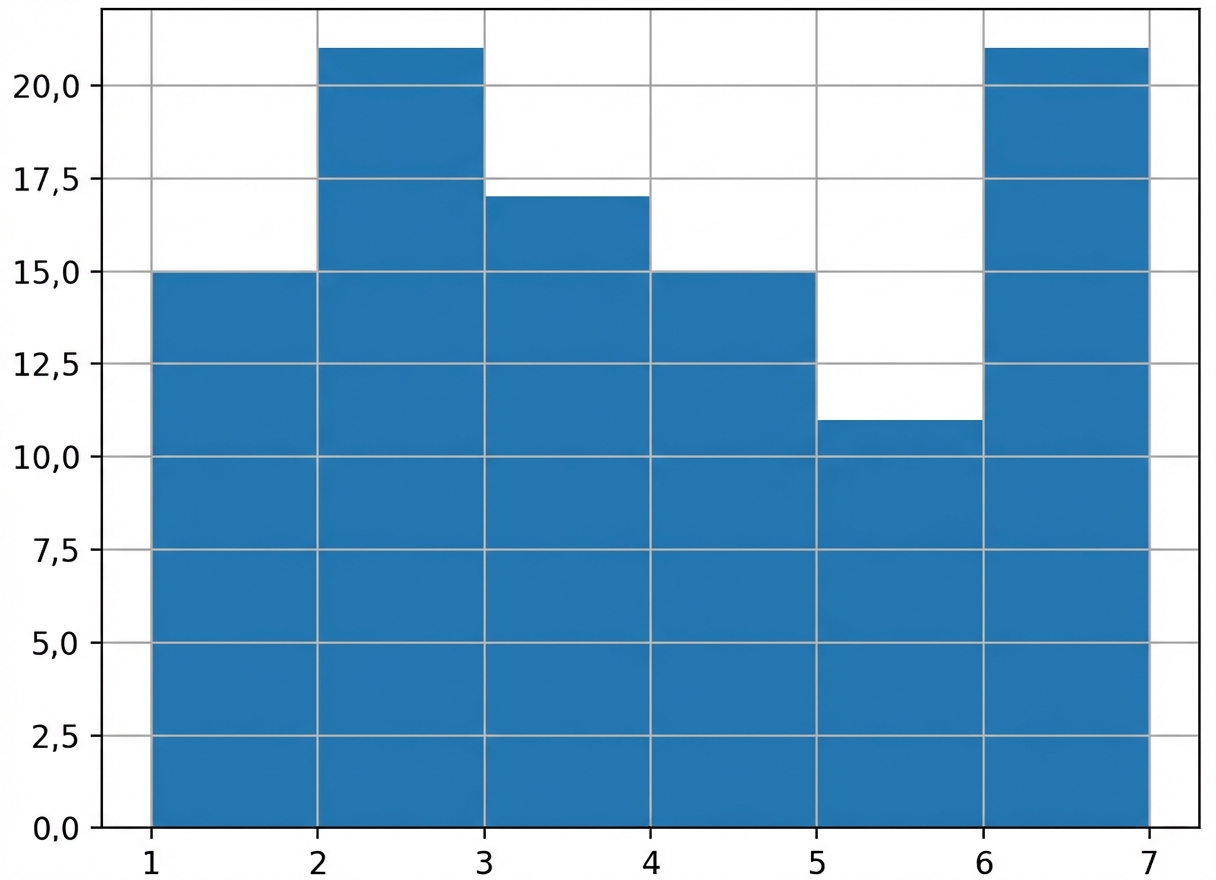
np.mean(rolls_100['number']) = 3.4
Theoretische Wahrscheinlichkeitsverteilung

mean(die['number']) = 3.5
Eine noch größere Stichprobe
Stichprobe mit 1000 Würfen
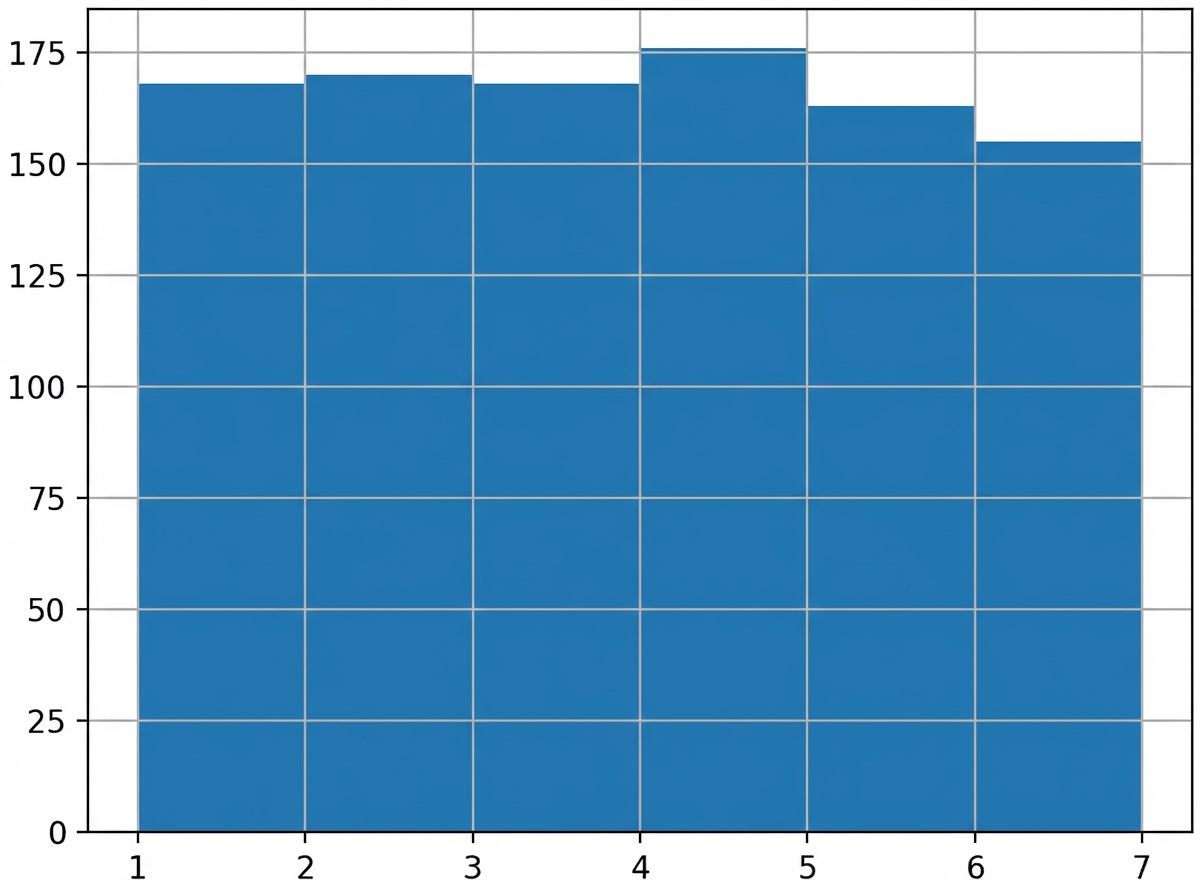
np.mean(rolls_1000['number']) = 3.48
Theoretische Wahrscheinlichkeitsverteilung

mean(die['number']) = 3.5
Gesetz der großen Zahlen
Mit zunehmender Stichprobengröße nähert sich der Stichprobenmittelwert dem Erwartungswert an.
| Stichprobengröße | Mittelwert |
|---|---|
| 10 | 3,00 |
| 100 | 3,40 |
| 1000 | 3,48 |
Lass uns üben!
Einführung in die Statistik in Python

