Korrelation
Einführung in die Statistik in Python

Maggie Matsui
Content Developer, DataCamp
Korrelation zwischen zwei Variablen
- x = erklärende/unabhängige Variable
- y = Reaktion/abhängige Variable
Korrelationskoeffizient
- Quantifiziert die lineare Beziehung zwischen zwei Variablen
- Zahl zwischen -1 und 1
- Die Größe entspricht der Stärke der Korrelation
- Das Vorzeichen (+ oder -) entspricht der Richtung der Beziehung
Größe = Stärke der Beziehung
0,99 (sehr starke Korrelation)
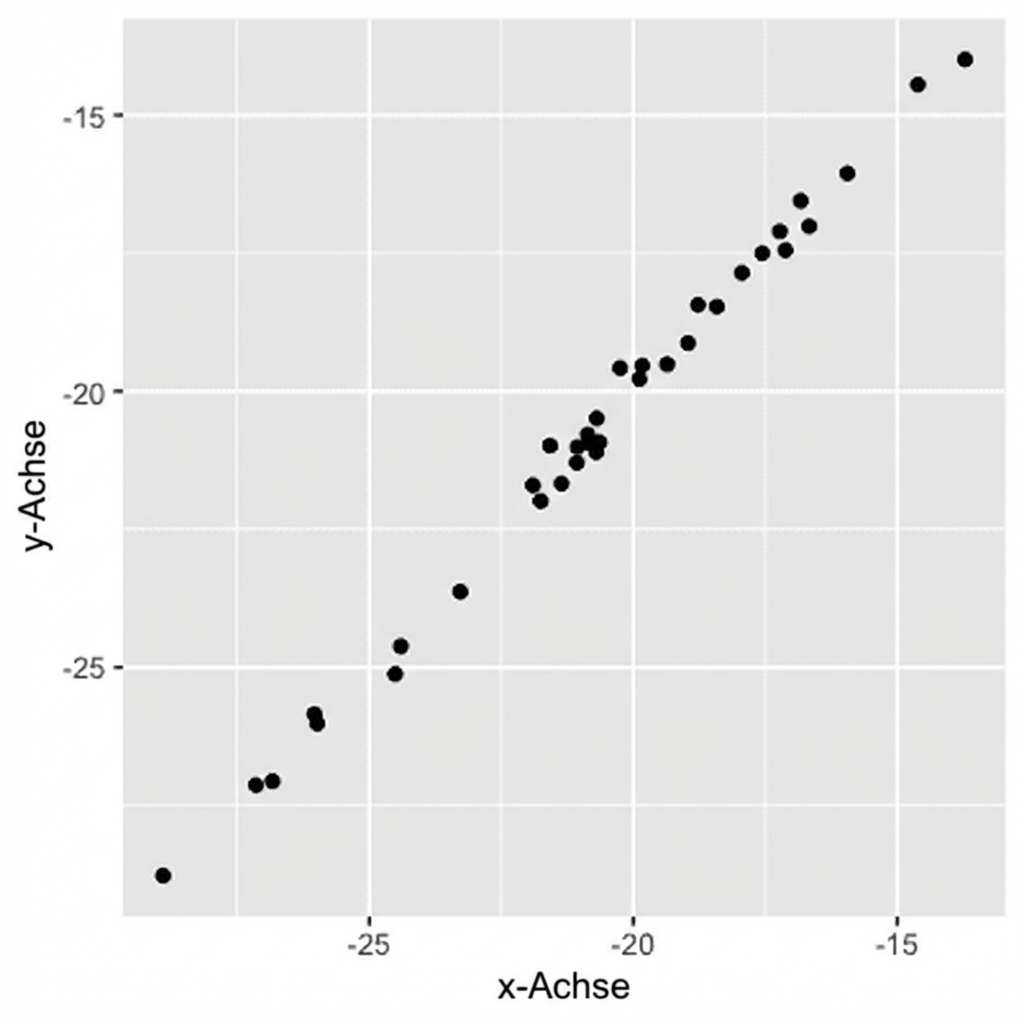
Größe = Stärke der Beziehung
0,99 (sehr starke Korrelation)

0,75 (starke Korrelation)
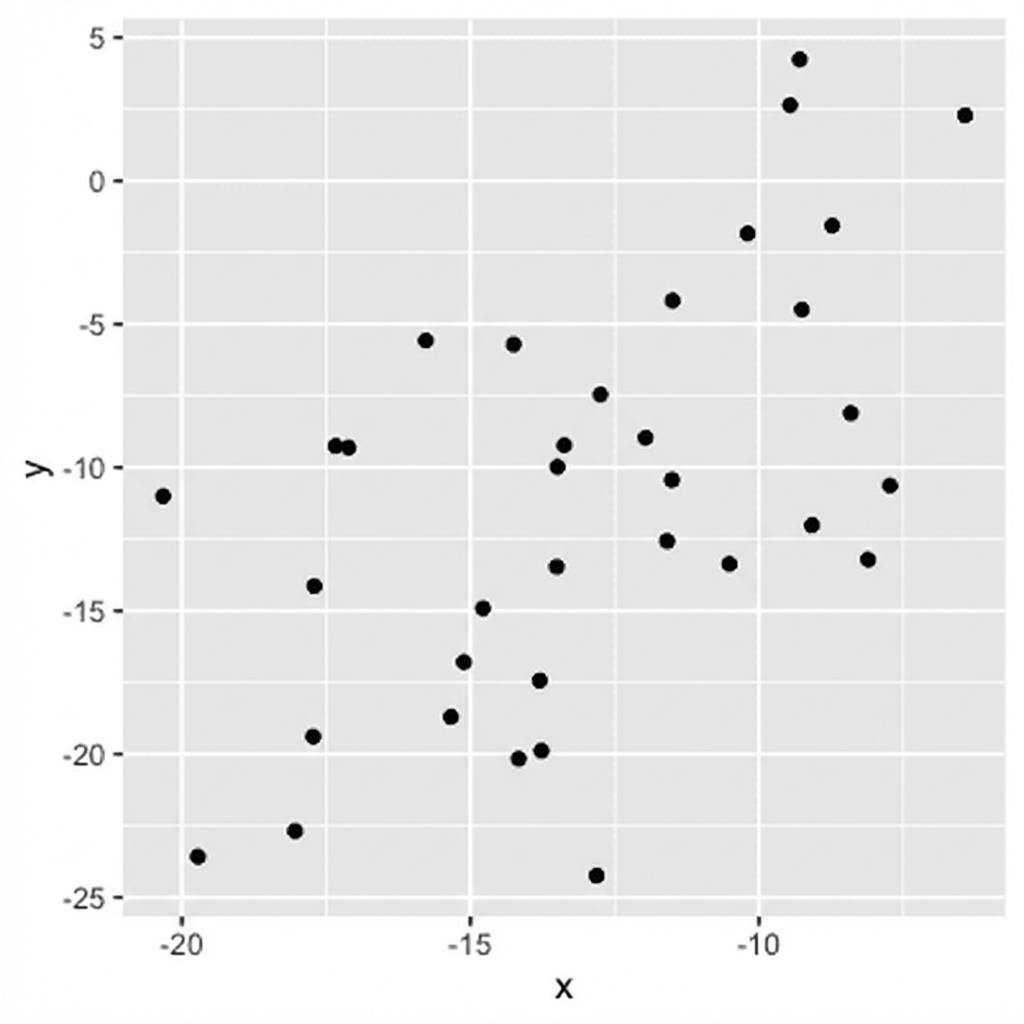
Größe = Stärke der Beziehung
0,56 (mäßige Korrelation)
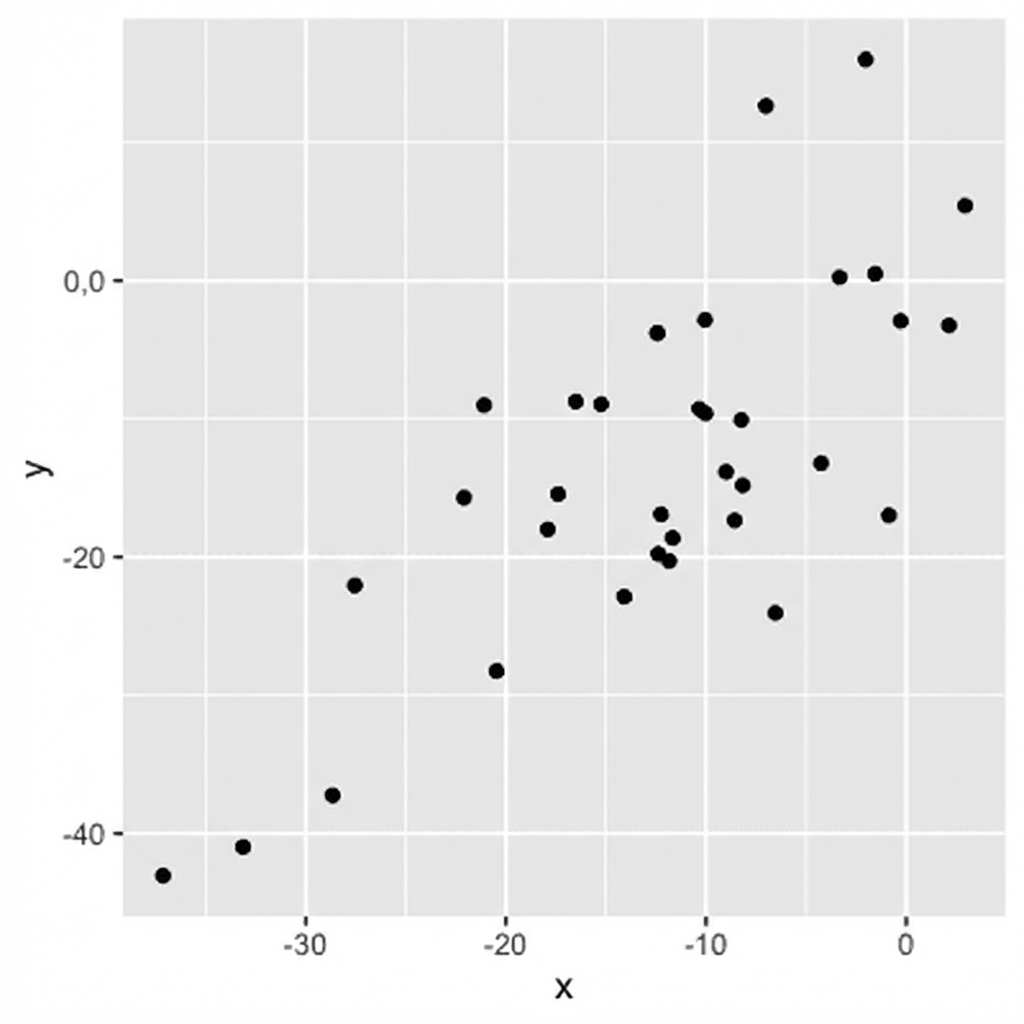
Größe = Stärke der Beziehung
0,56 (mäßige Korrelation)

0,21 (schwache Korrelation)
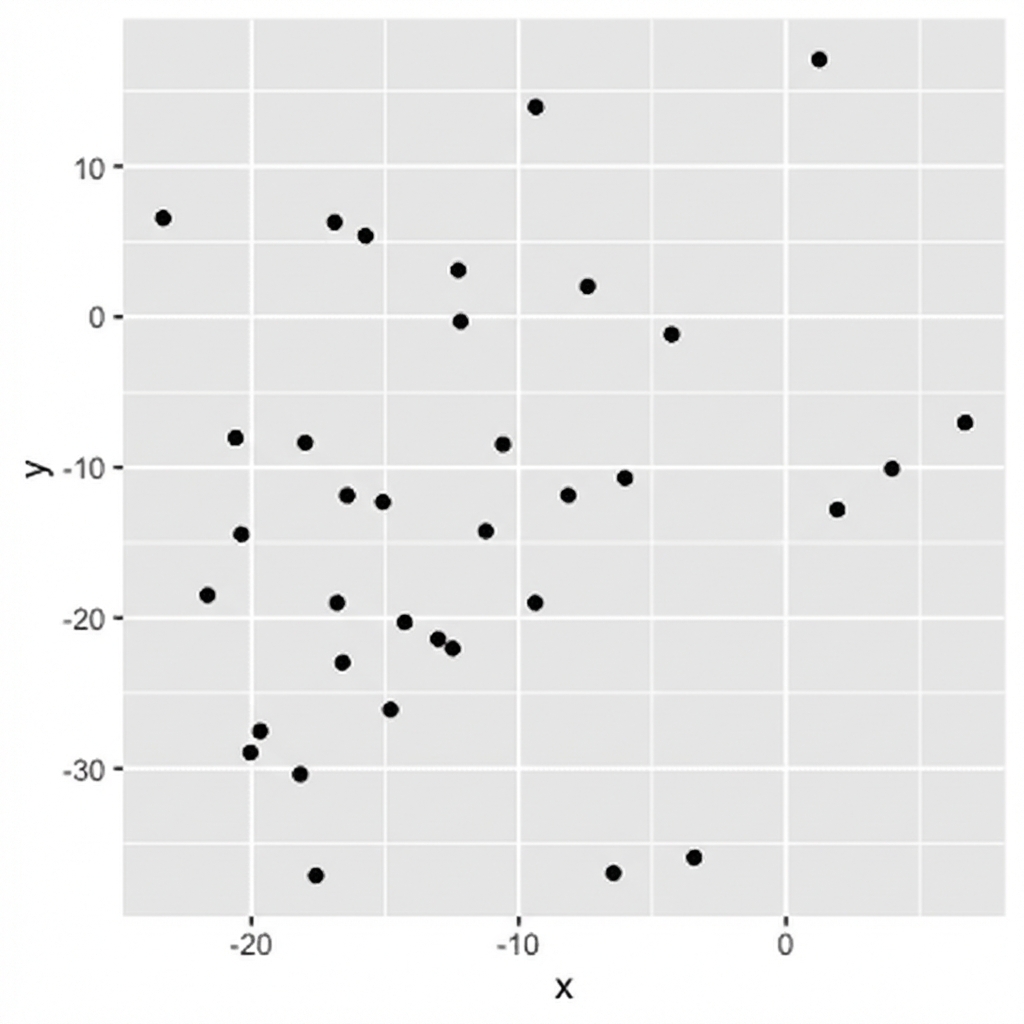
Größe = Stärke der Beziehung
0,04 (keine Korrelation)
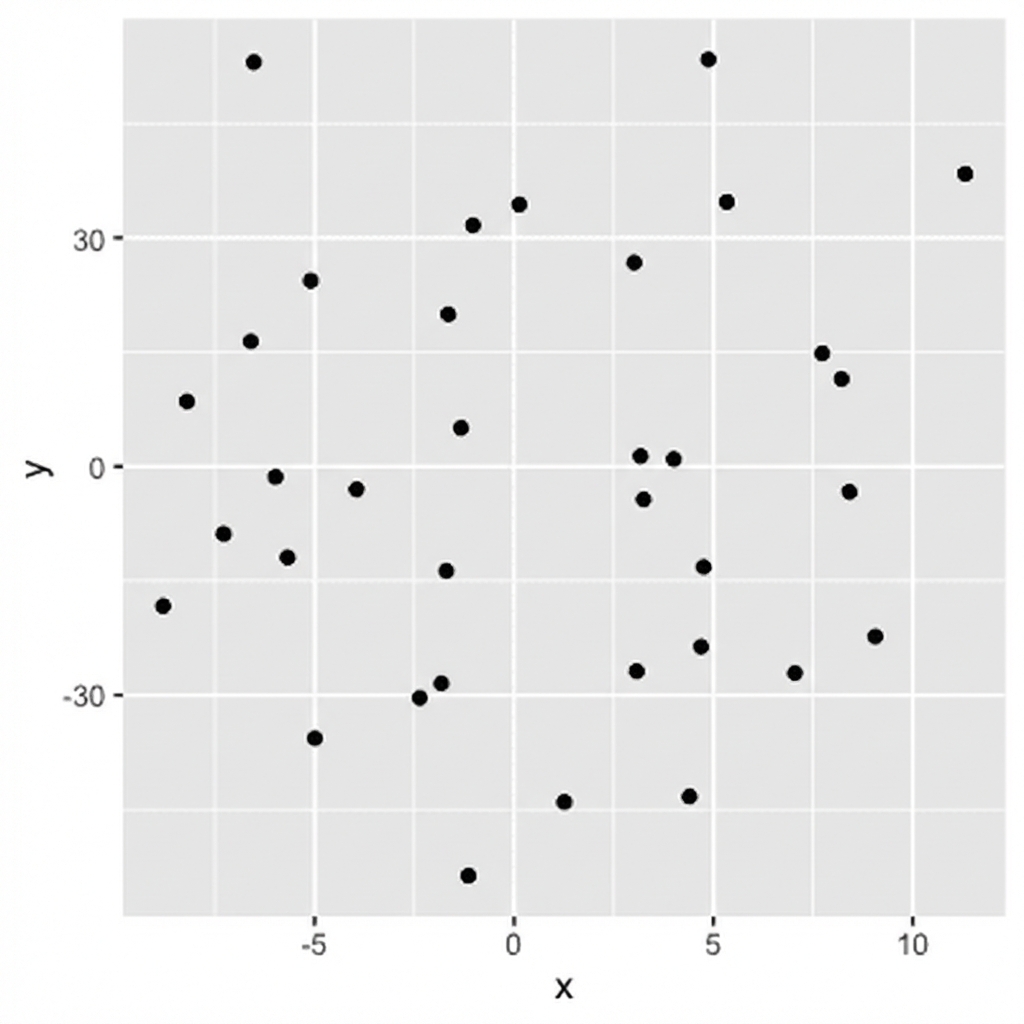
- Die Kenntnis des Wertes von
xsagt uns nichts überyaus
Vorzeichen = Richtung
0,75: wenn x steigt, steigt y

-0,75: wenn x steigt, sinkt y
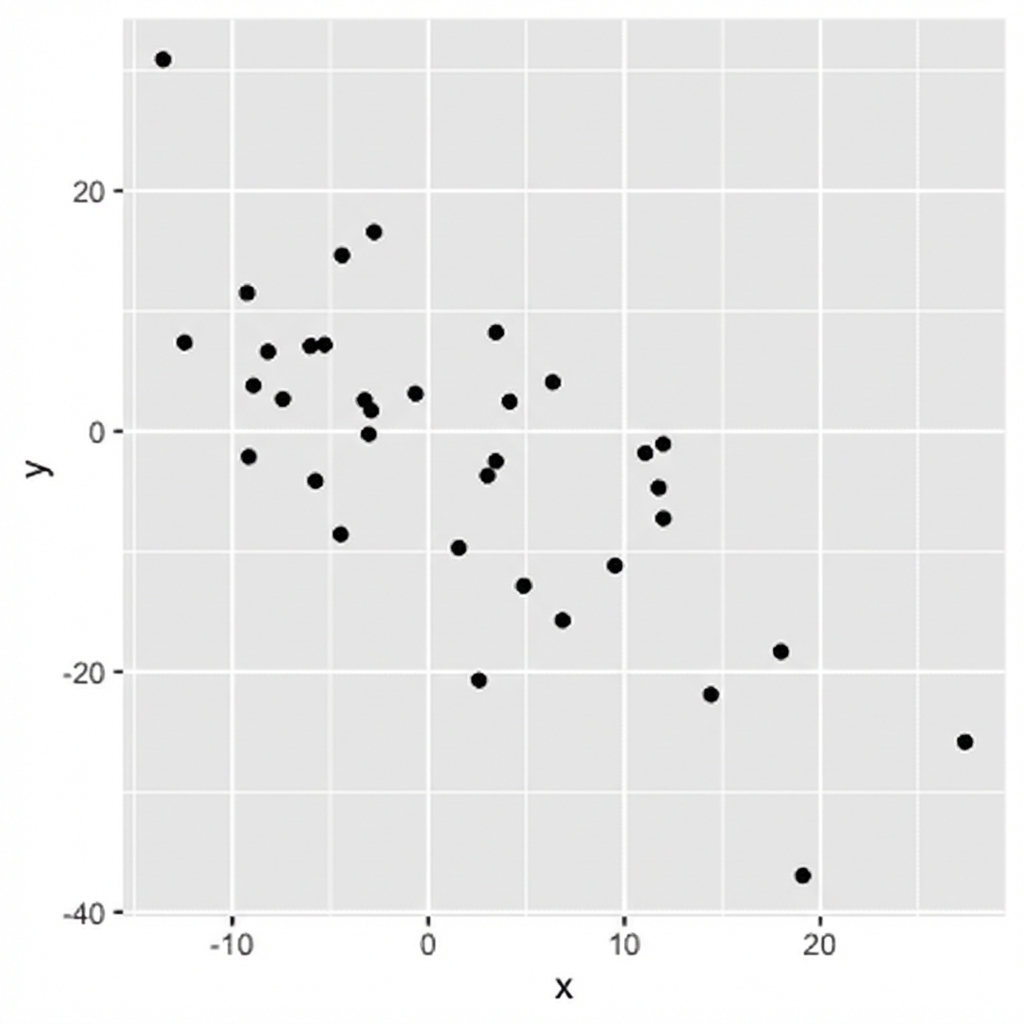
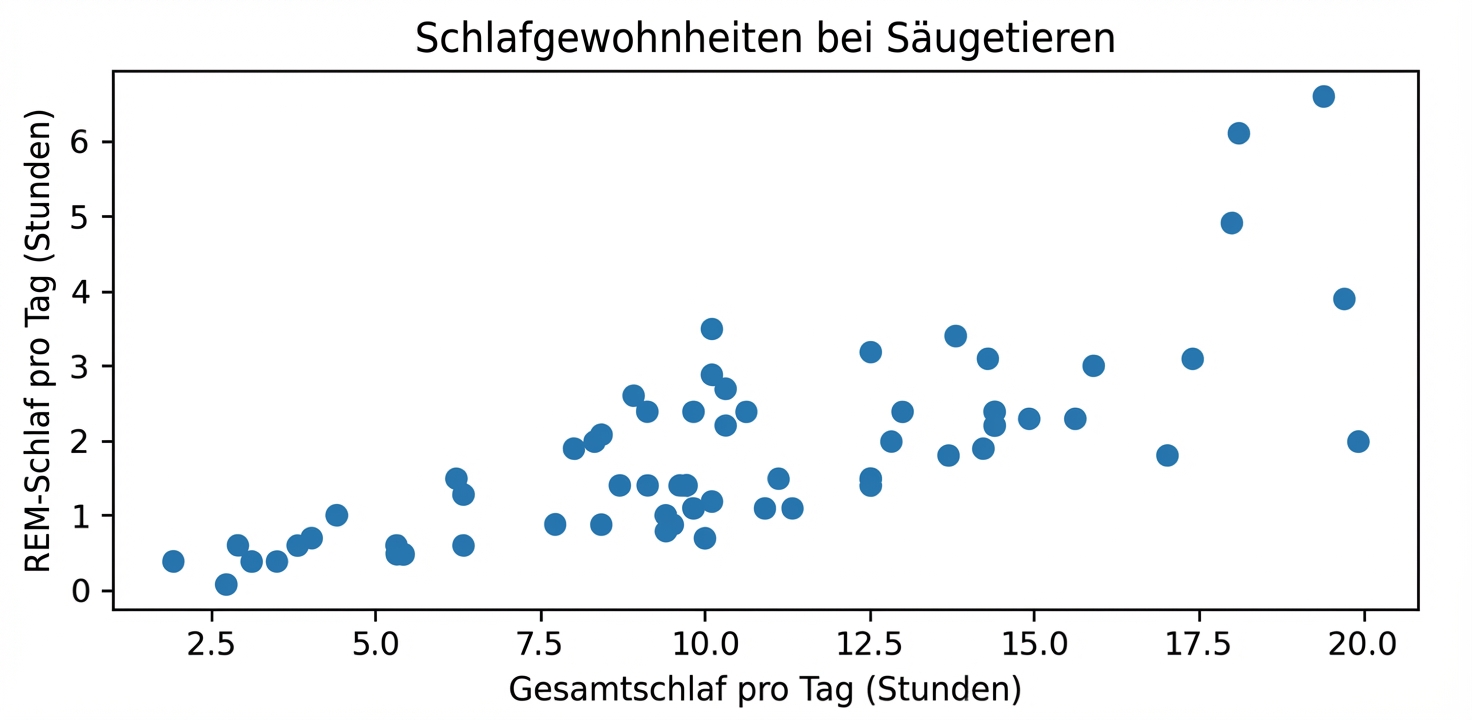
Beziehungen visualisieren
import seaborn as snssns.scatterplot(x="sleep_total", y="sleep_rem", data=msleep)plt.show()
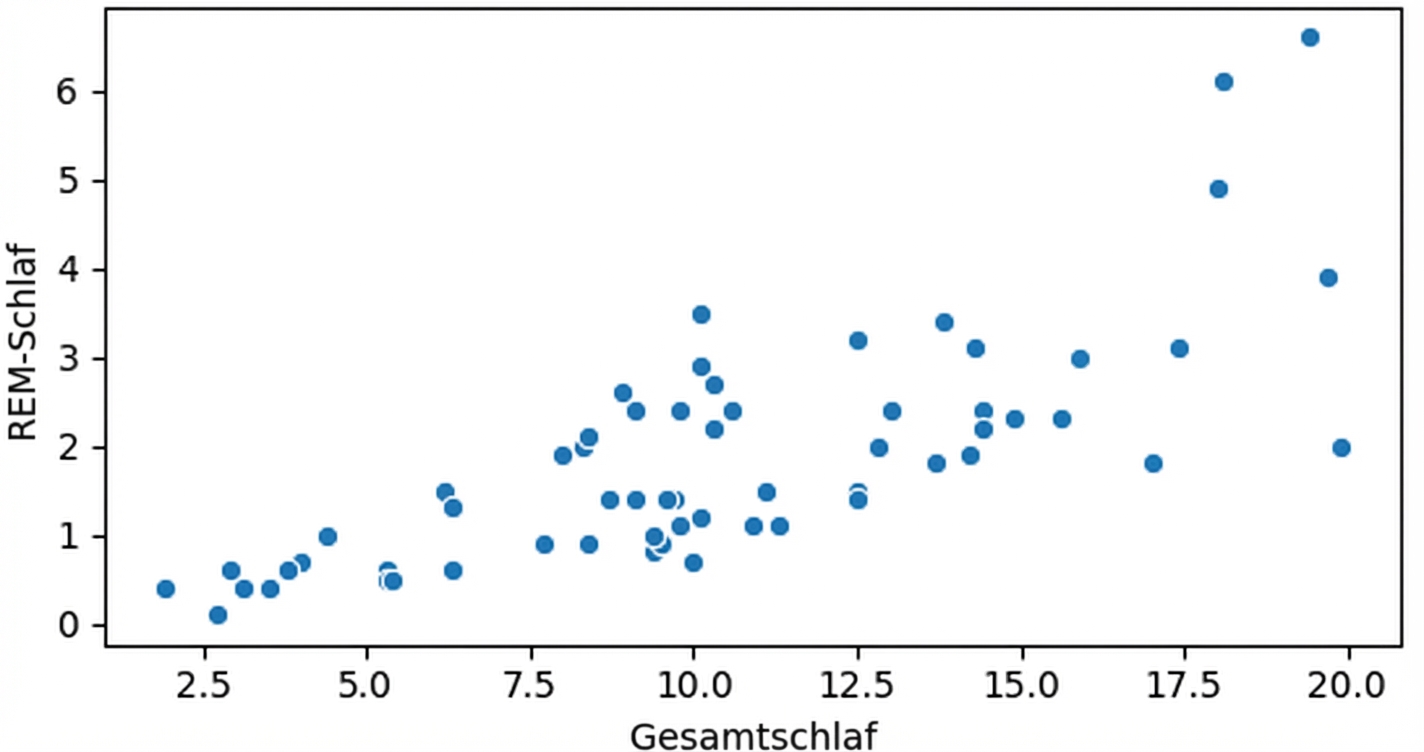
Hinzufügen einer Trendlinie
import seaborn as sns sns.lmplot(x="sleep_total", y="sleep_rem", data=msleep, ci=None)plt.show()
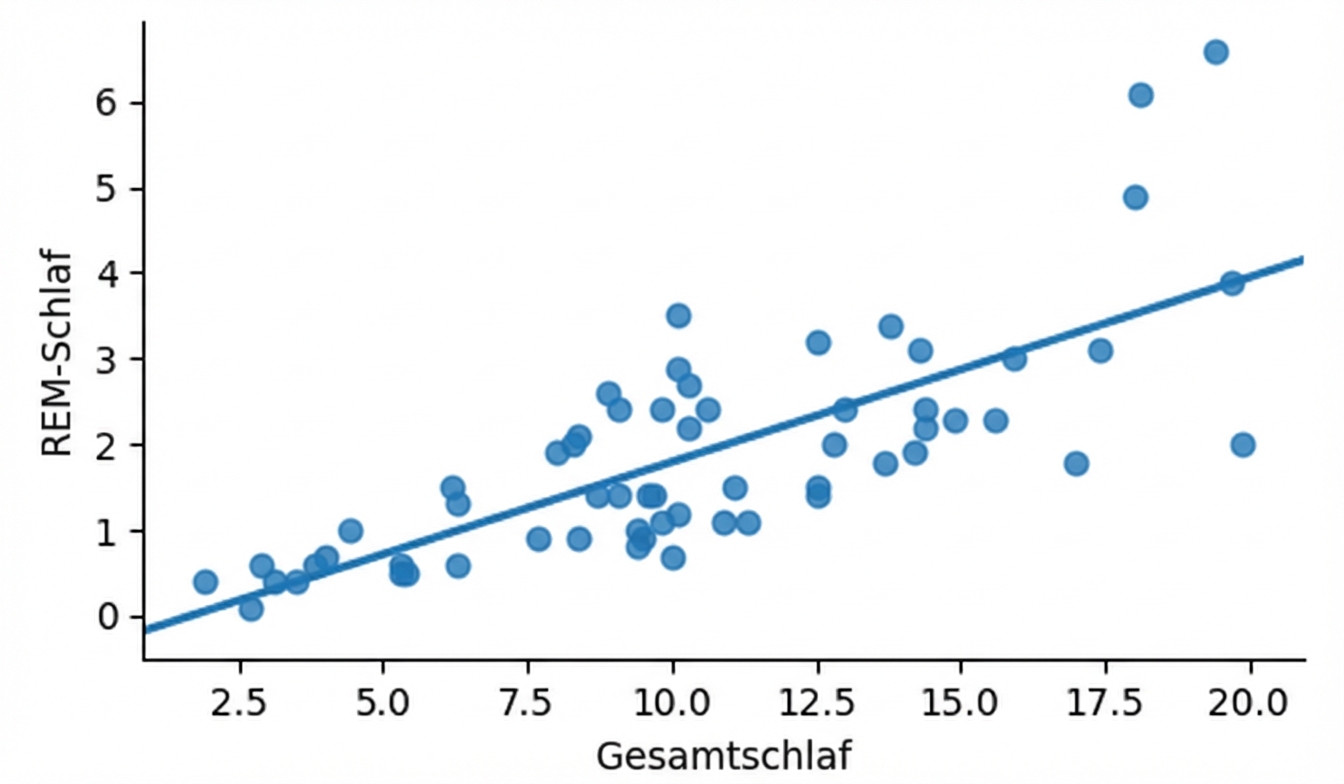
Berechnung der Korrelation
msleep['sleep_total'].corr(msleep['sleep_rem'])
0.751755
msleep['sleep_rem'].corr(msleep['sleep_total'])
0.751755
Viele Wege zur Berechnung der Korrelation
- In diesem Kurs verwendet: Pearson Produkt-Moment-Korrelation ($r$)
- Am häufigsten verwendet
- $\bar{x} =$ Mittelwert von $x$
- $\sigma_x =$ Standardabweichung von $x$
$$ r = \frac{1}{n - 1} \sum_{i=1}^{n} \frac{(x_i - \bar{x})(y_i - \bar{y})}{\sigma_x \cdot \sigma_y}$$
- Varianten dieser Formel:
- Kendall's Tau
- Spearman’sche Rangkorrelationskoeffizient
Lass uns üben!
Einführung in die Statistik in Python

