Grenzen bei der Korrelation
Einführung in die Statistik in R

Maggie Matsui
Content Developer, DataCamp
Nicht-lineare Beziehungen
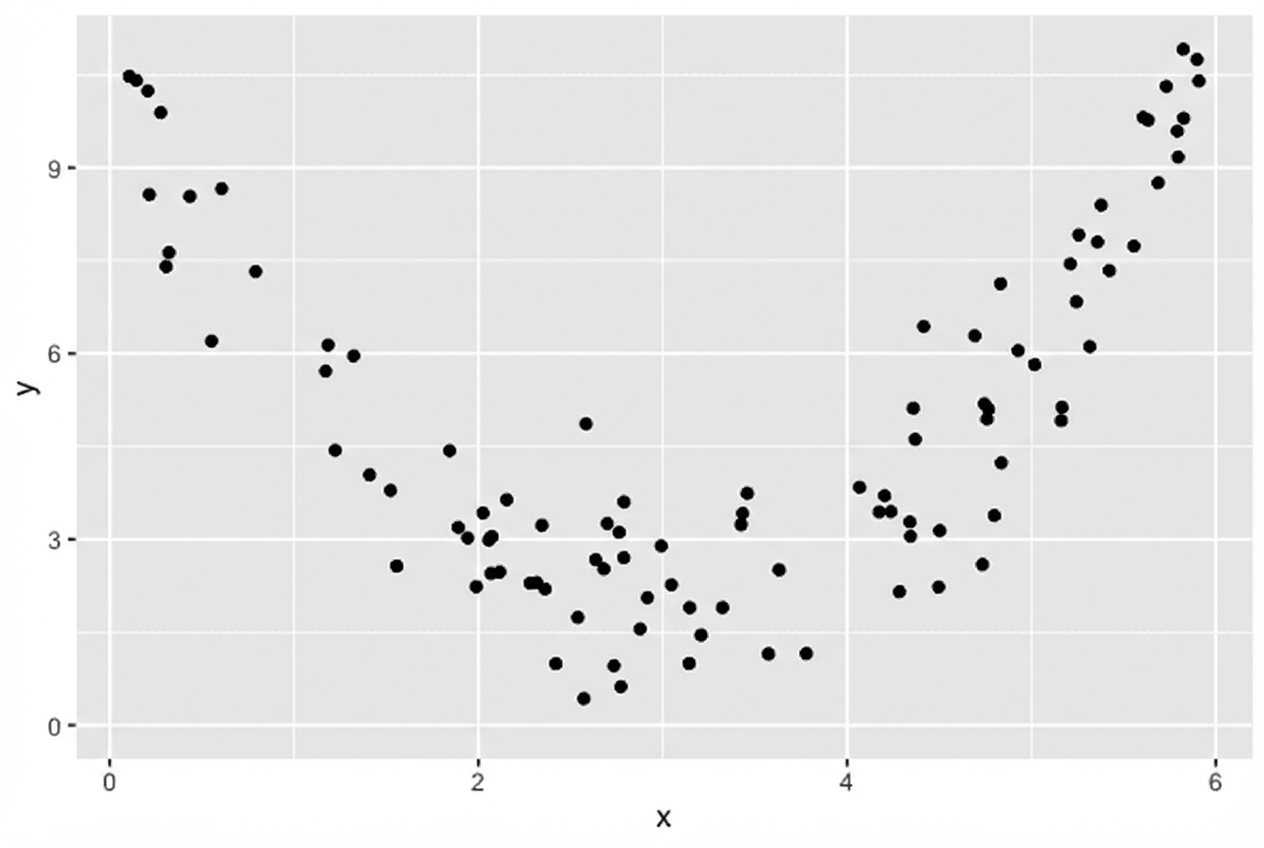
$$r = 0.18$$
Nicht-lineare Beziehungen
Was wir sehen:
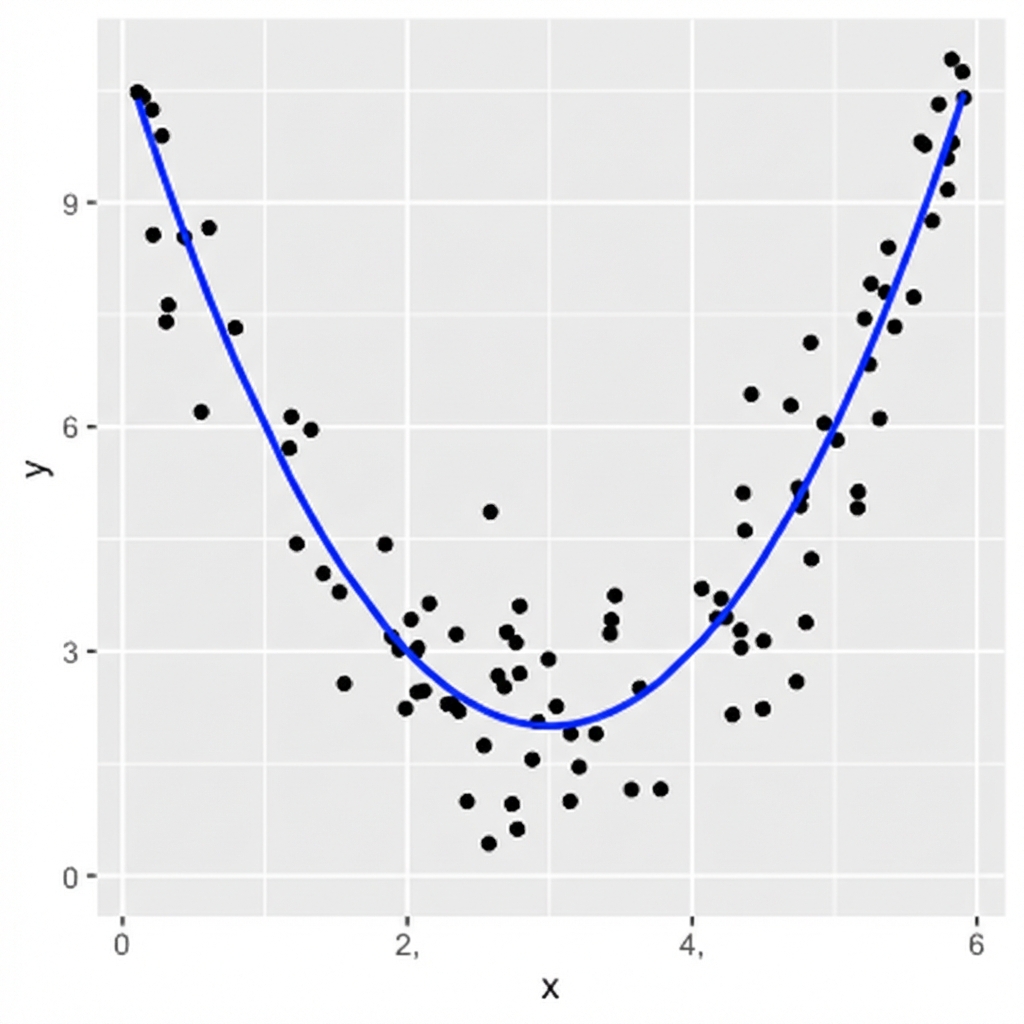
Was der Korrelationskoeffizient sieht:
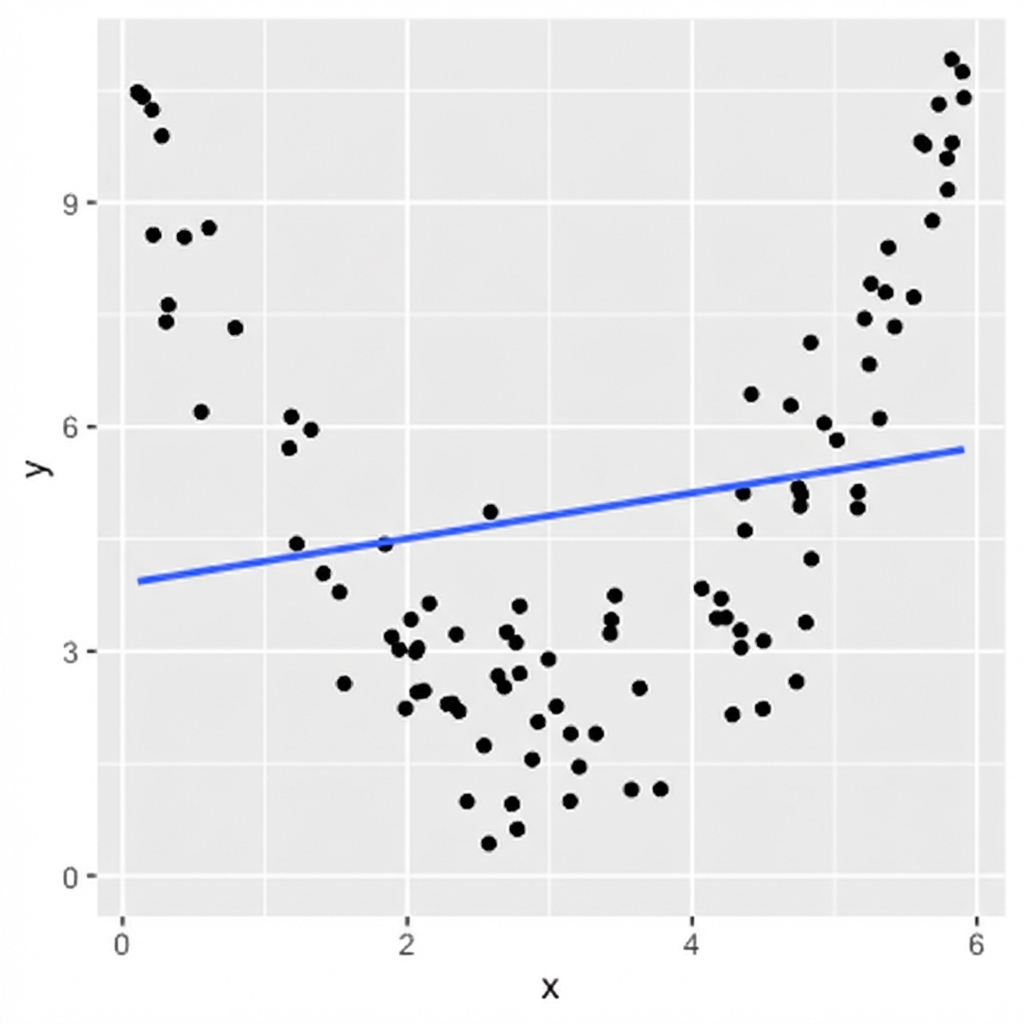
Die Korrelation berücksichtigt nur lineare Beziehungen
Korrelation sollte nicht blind verwendet werden
cor(df$x, df$y)
0.1786163
Visualisiere deine Daten immer

Daten zum Schlaf von Säugetieren
msleep
name vore sleep_total awake bodywt
1 Cheetah carni 12.1 11.9 50
2 Owl monkey omni 17 7 0.48
3 Mountain beaver herbi 14.4 9.6 1.35
4 Greater short-tailed shrew omni 14.9 9.1 0.019
5 Cow herbi 4 20 600
6 Three-toed sloth herbi 14.4 9.6 3.85
...
Körpergewicht vs. Wachzeit
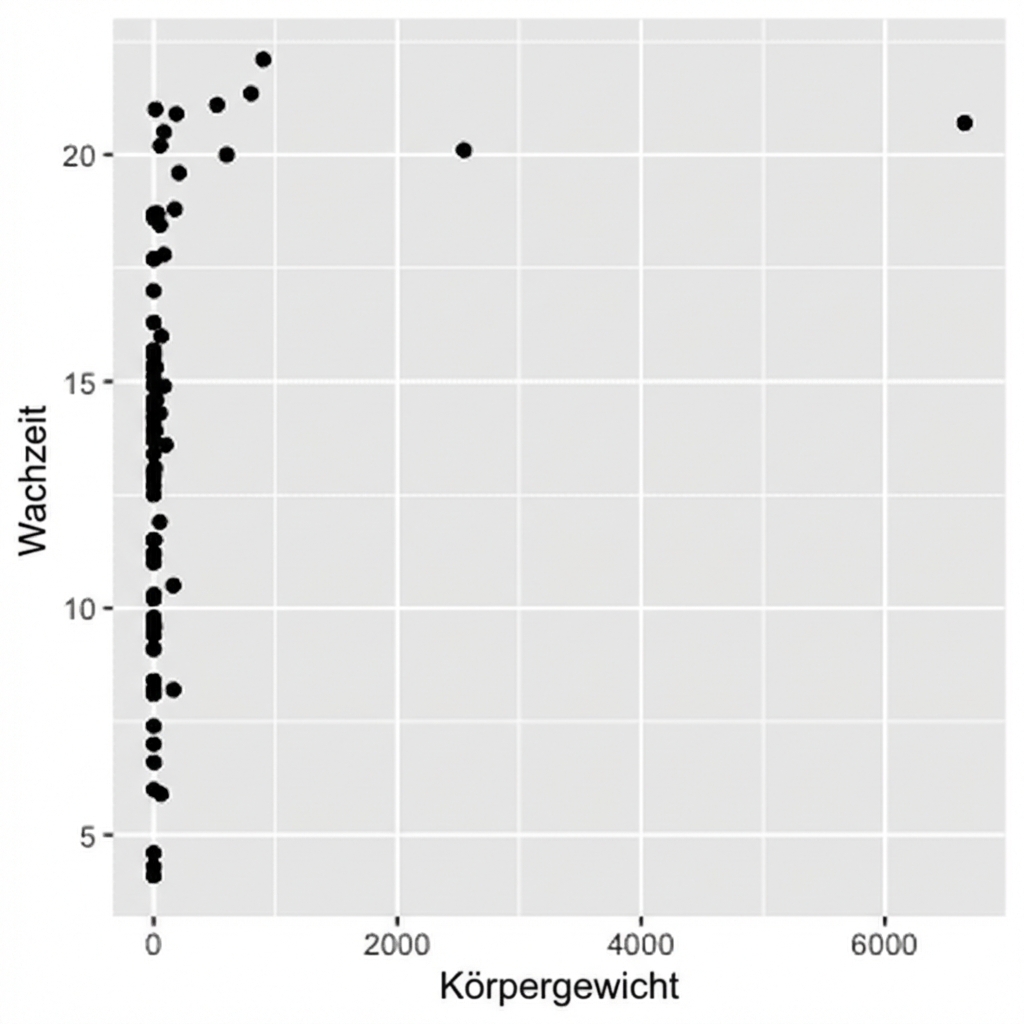
cor(msleep$bodywt, msleep$awake)
0.3119801
Verteilung des Körpergewichts
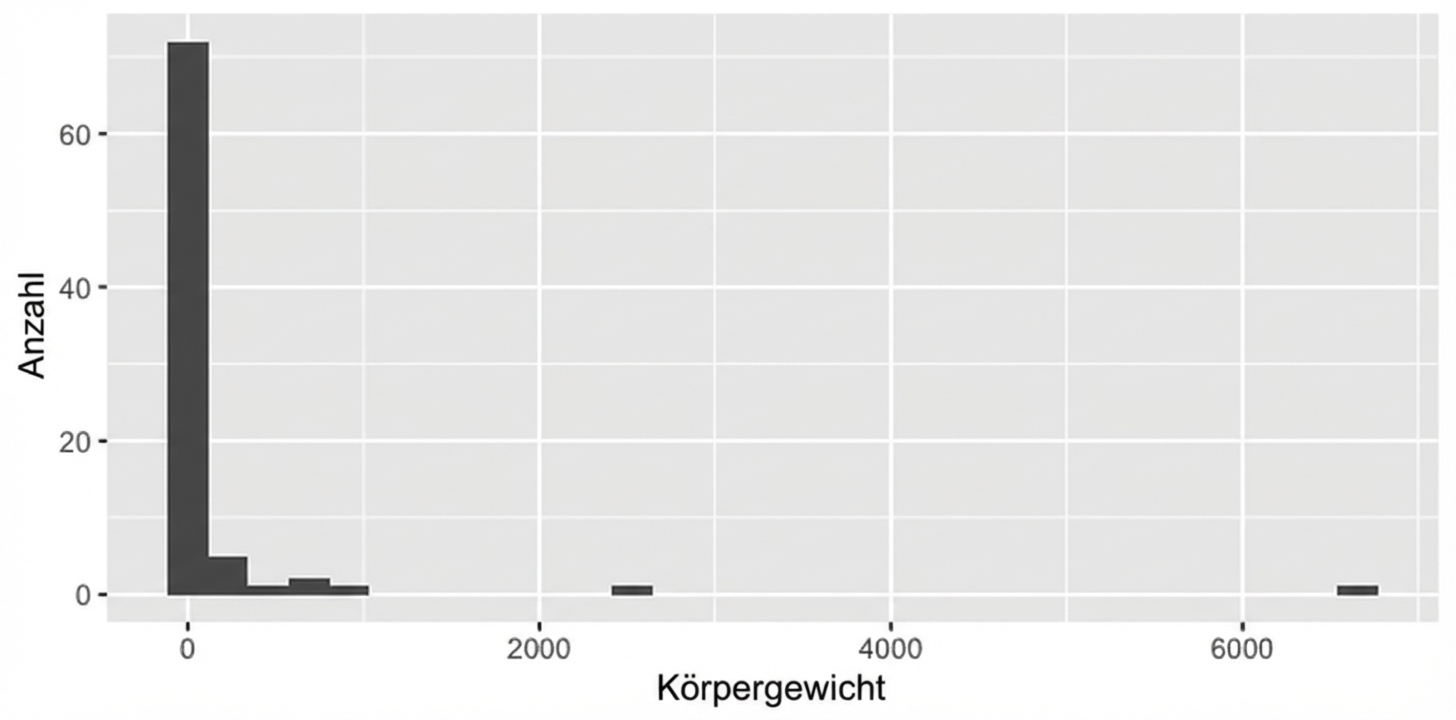
Log-Transformation
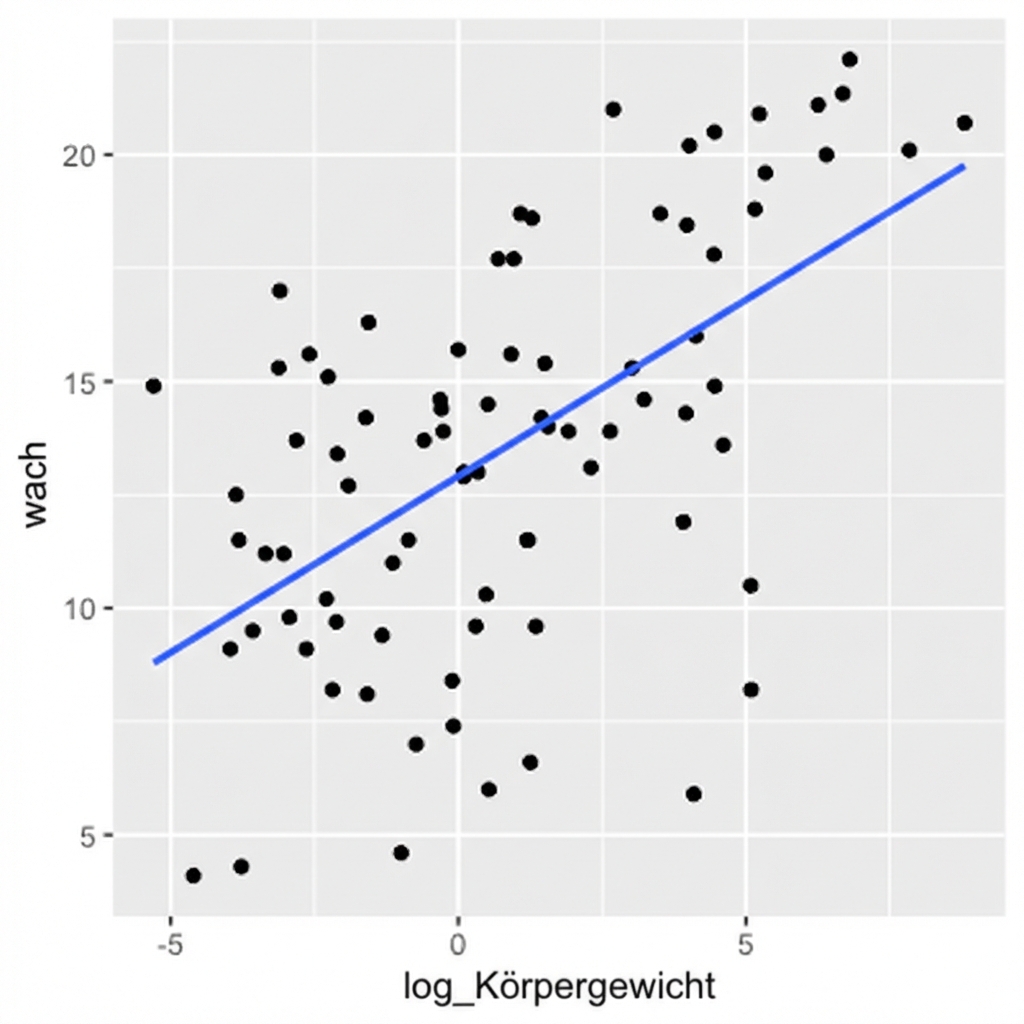
msleep %>% mutate(log_bodywt = log(bodywt)) %>%ggplot(aes(log_bodywt, awake)) + geom_point() + geom_smooth(method = "lm", se = FALSE)
cor(msleep$log_bodywt, msleep$awake)
0.5687943
Andere Transformationen
- Log-Transformation (
log(x)) - Quadratwurzel-Transformation (
sqrt(x)) Reziproke Transformation (
1 / x)Kombinationen davon, z. B.:
log(x)undlog(y)sqrt(x)und1 / y
Wozu verwendet man eine Transformation?
- Bestimmte statistische Methoden setzen voraus, dass die Variablen eine lineare Beziehung haben
- Korrelationskoeffizient
- Lineare Regression
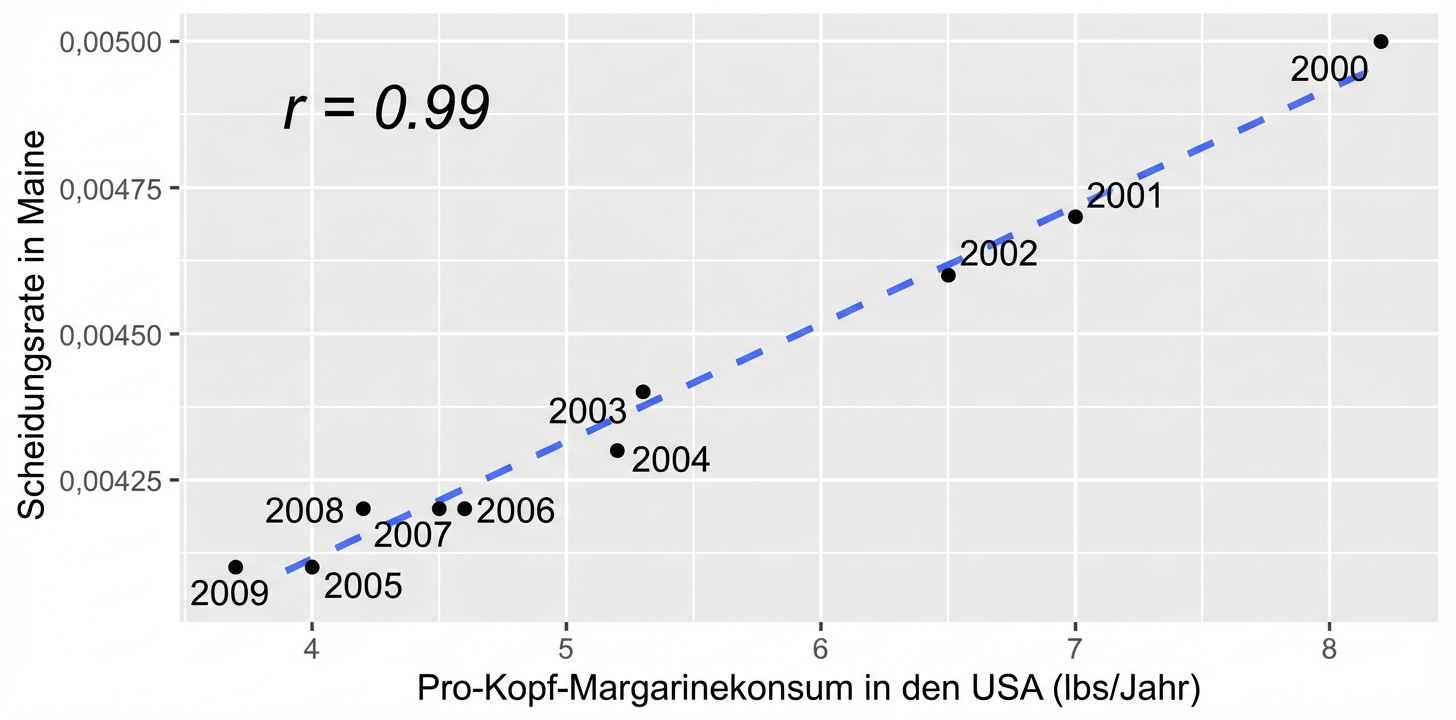
Korrelation bedeutet nicht gleich Kausalität
xkorreliert mit y bedeutet nicht, dass x`y` verursacht
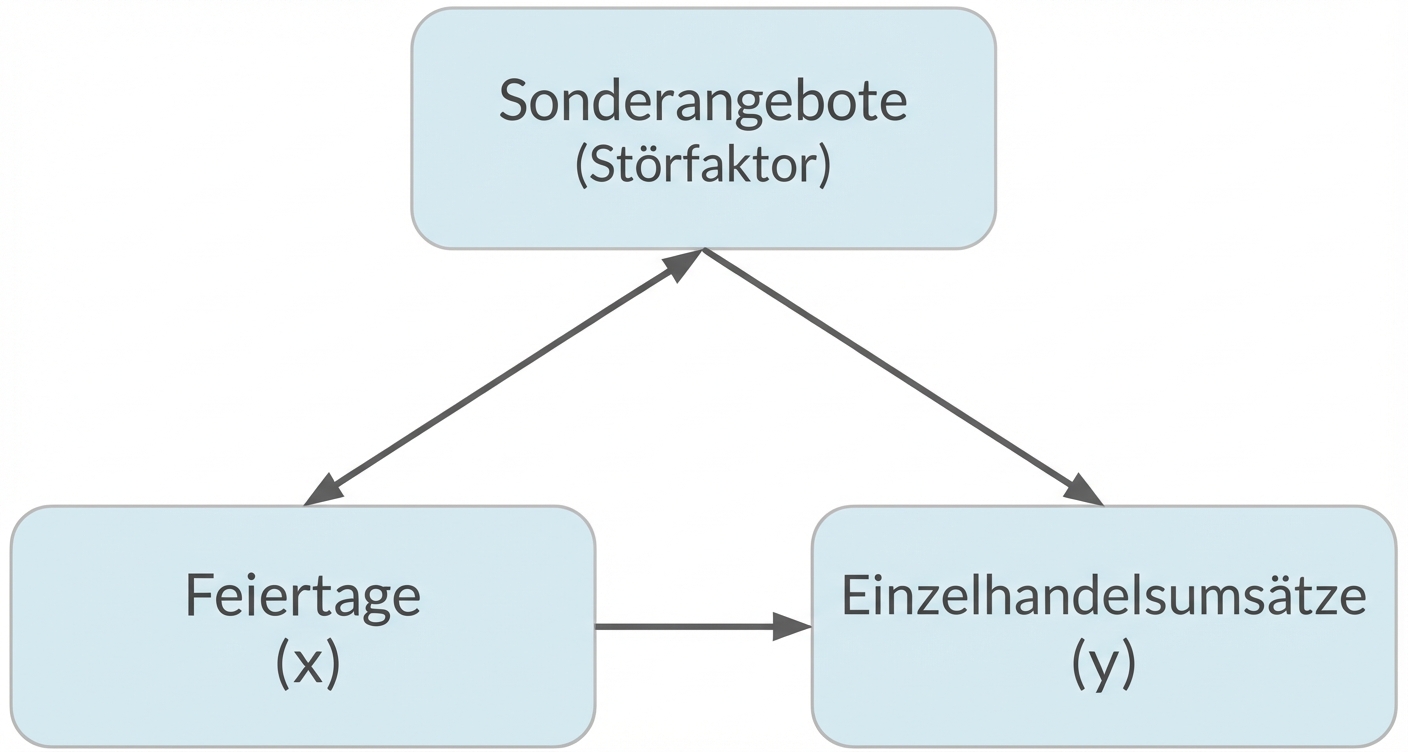
Verzerrungen
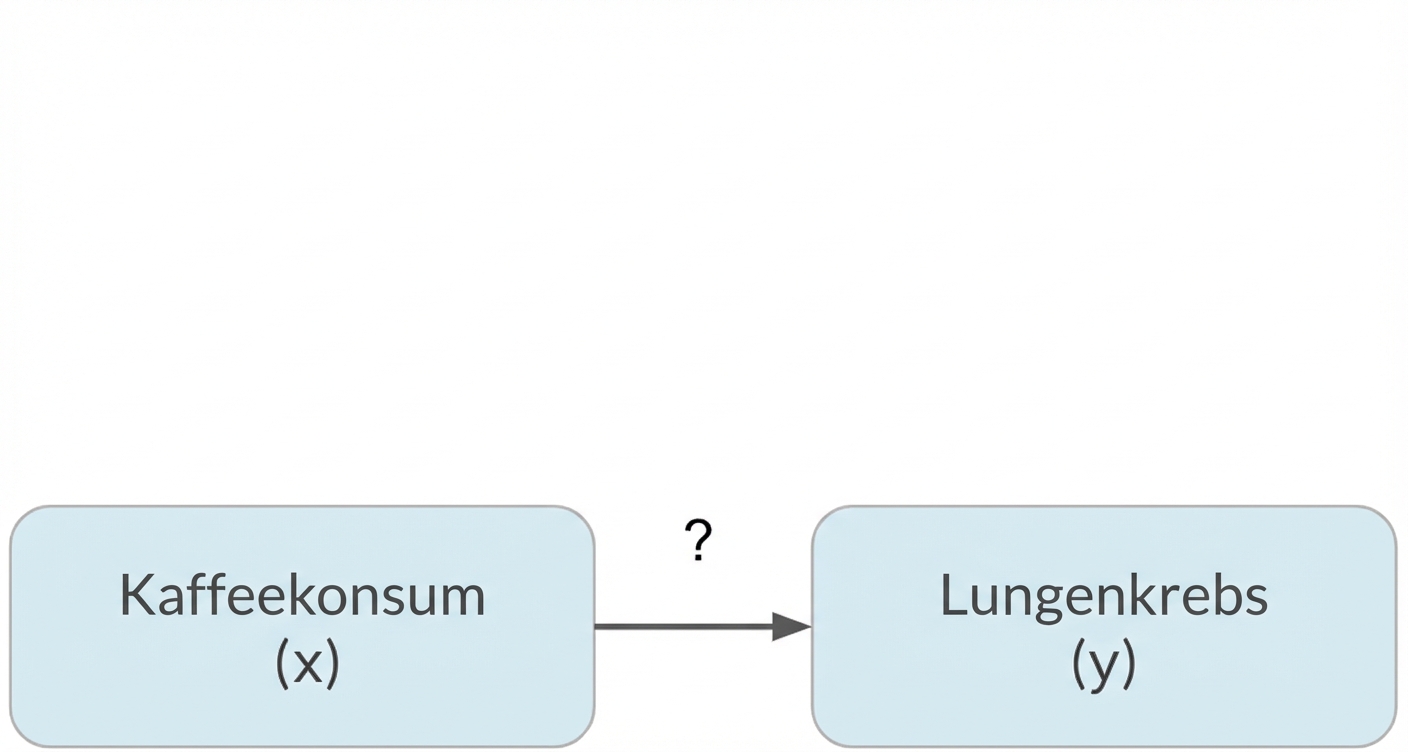
Verzerrungen
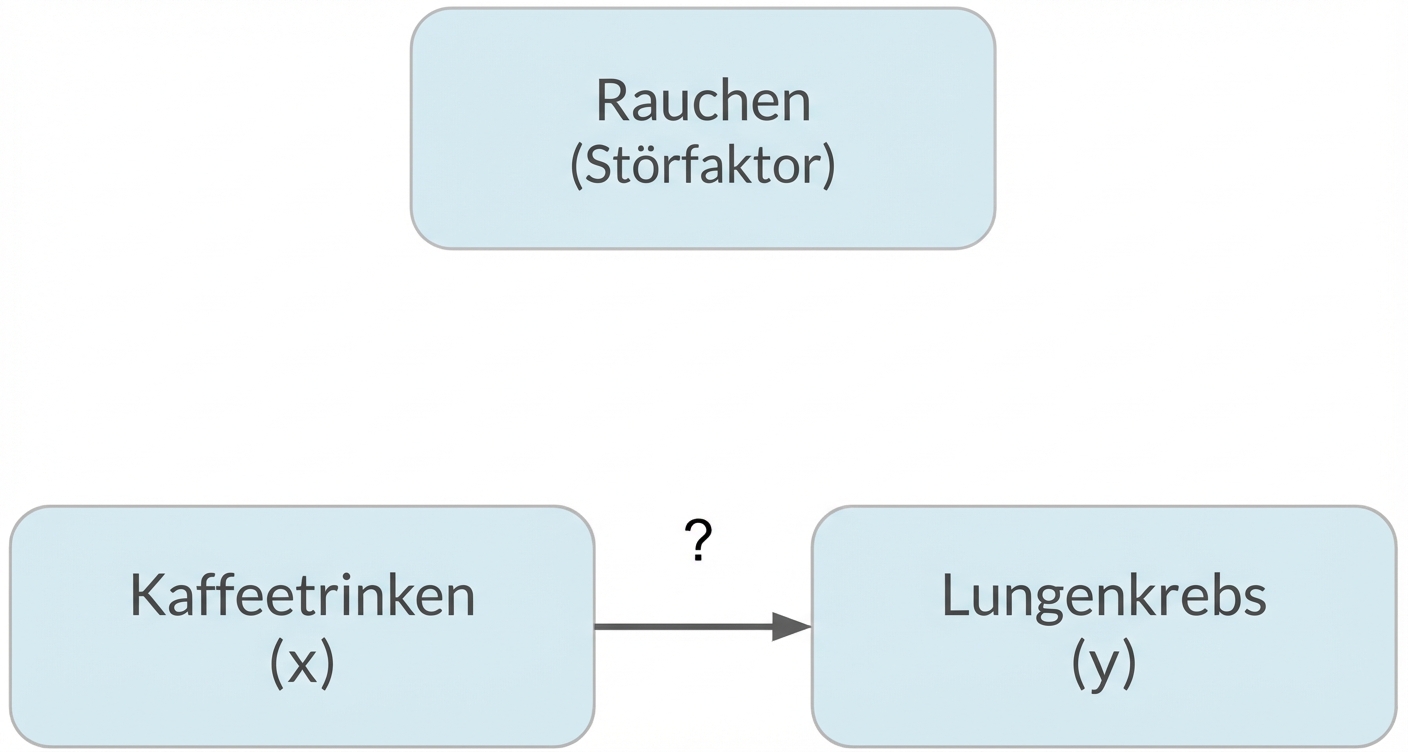
Verzerrungen
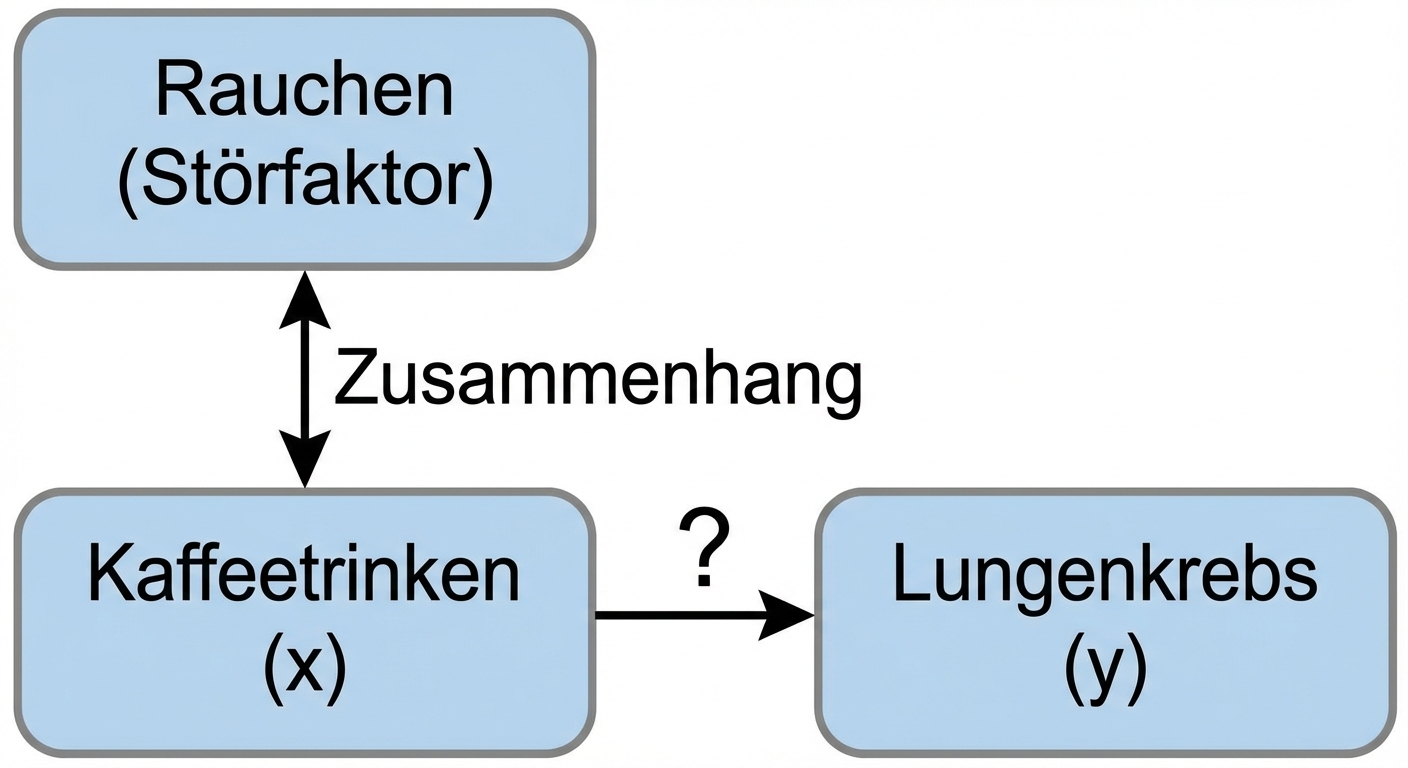
Verzerrungen
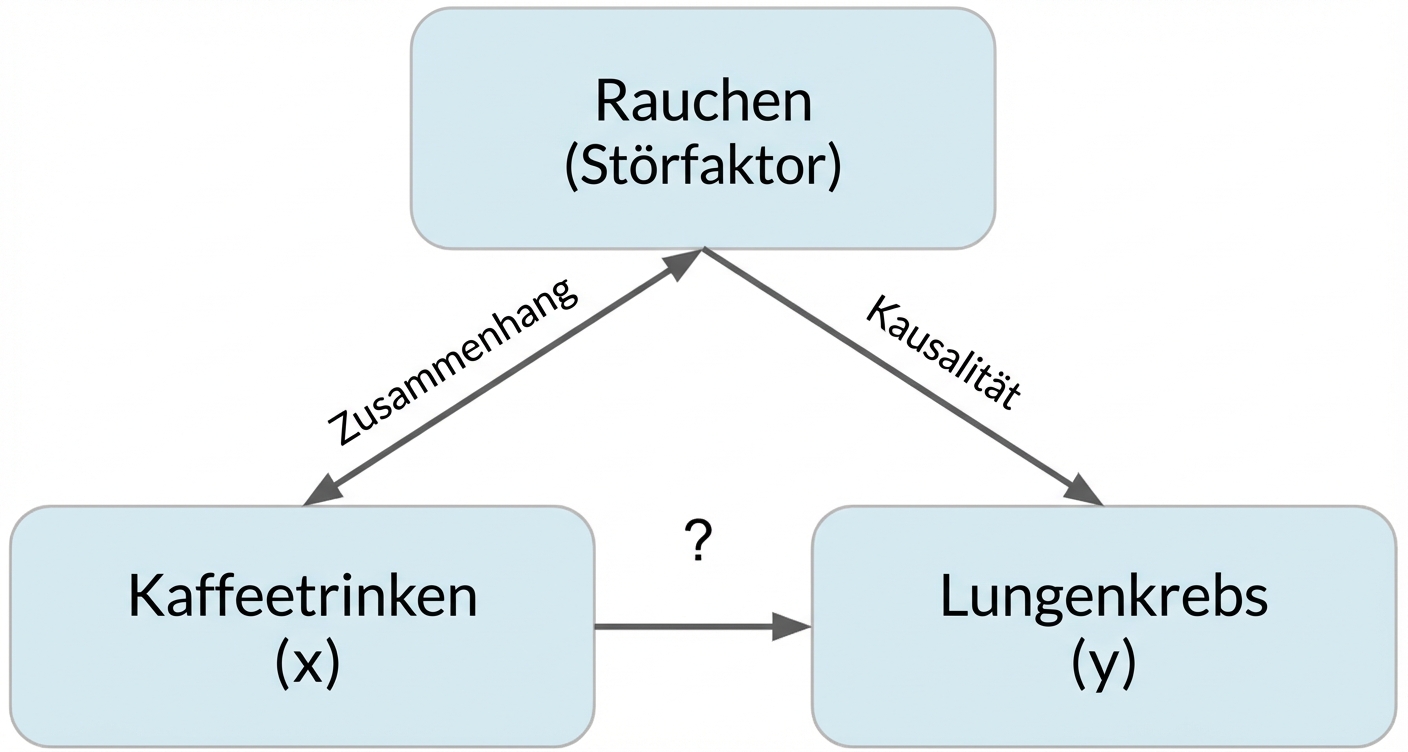
Verzerrungen
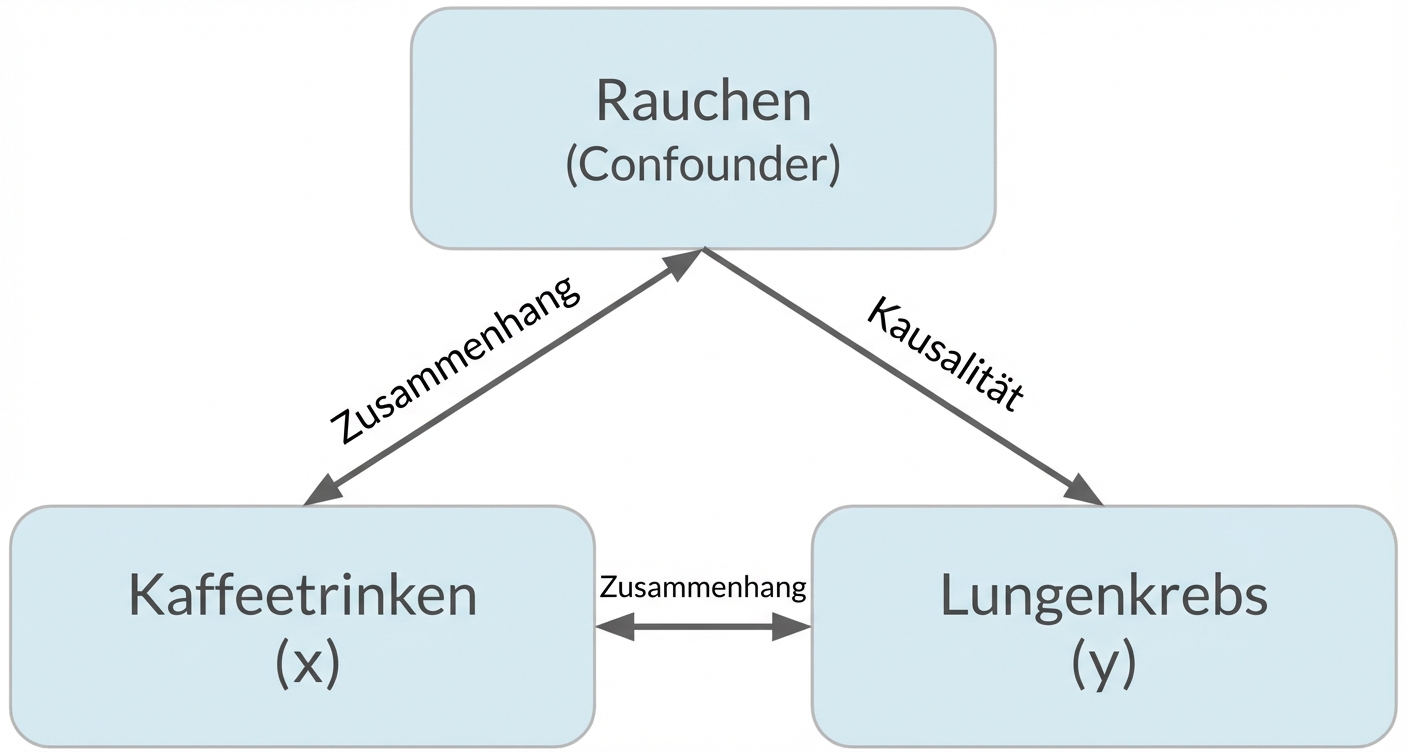
Lass uns üben!
Einführung in die Statistik in R

