Korrelation
Einführung in die Statistik in R

Maggie Matsui
Content Developer, DataCamp
Korrelation zwischen zwei Variablen
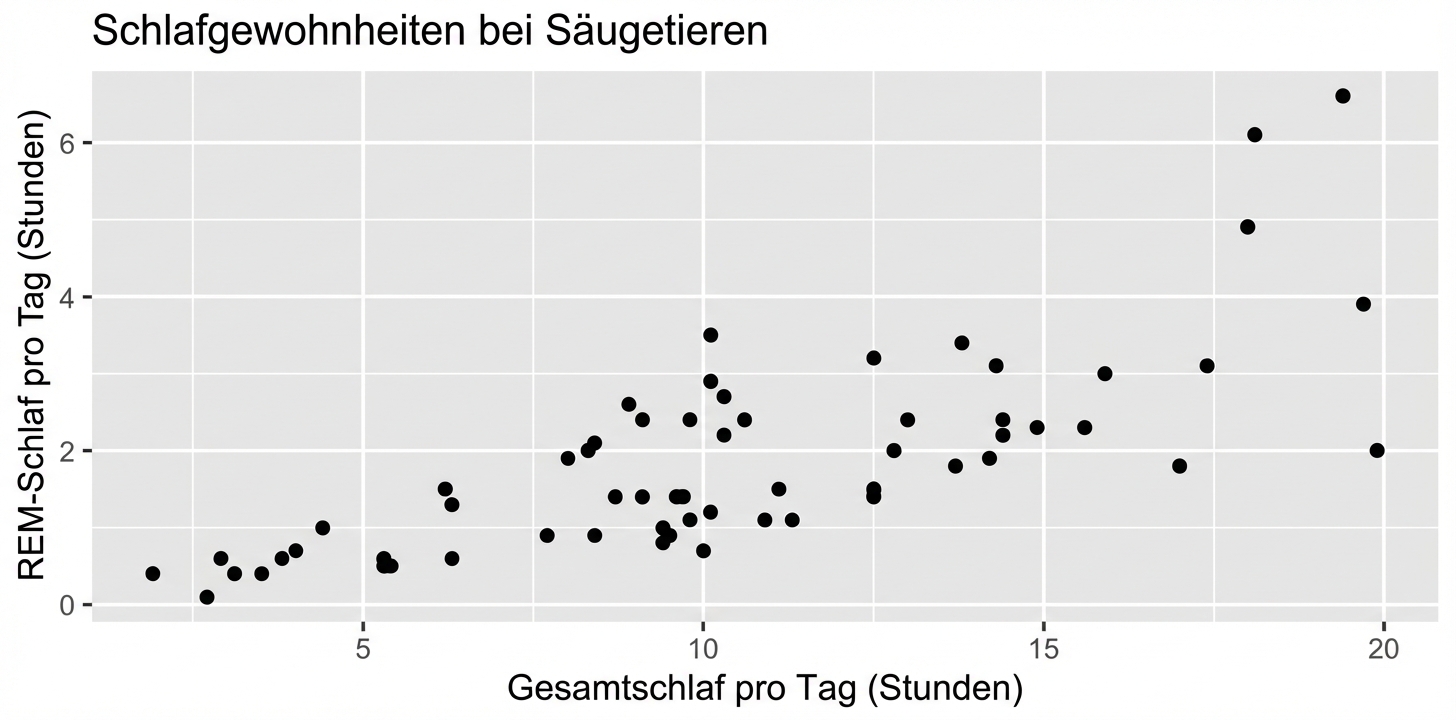
- x = erklärende/unabhängige Variable
- y = Reaktion/abhängige Variable
Korrelationskoeffizient
- Quantifiziert die lineare Beziehung zwischen zwei Variablen
- Zahl zwischen -1 und 1
- Das Ausmaß entspricht der Stärke der Korrelation
- Das Vorzeichen (+ oder -) entspricht der Richtung der Beziehung
Ausmaß = Stärke der Beziehung
0,99 (sehr starke Korrelation)
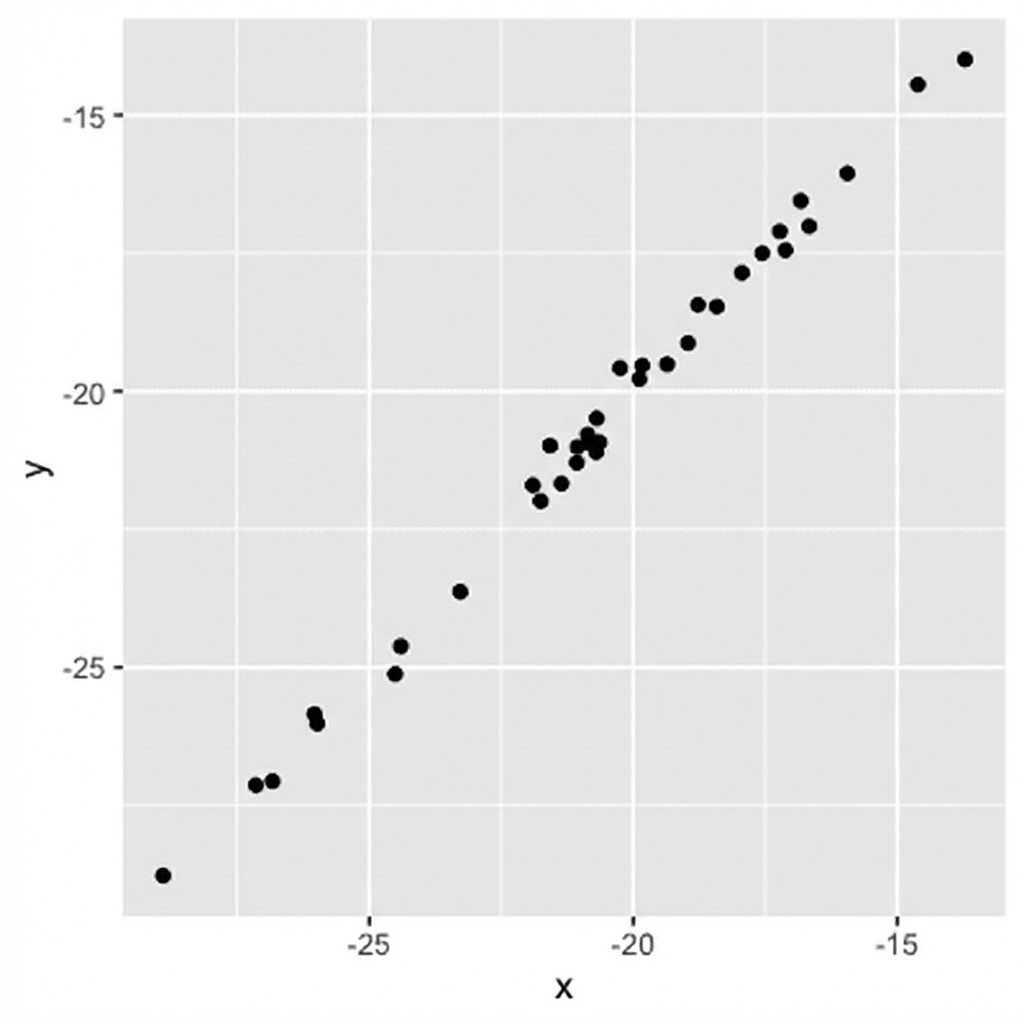
Ausmaß = Stärke der Beziehung
0,99 (sehr starke Korrelation)

0,75 (starke Korrelation)
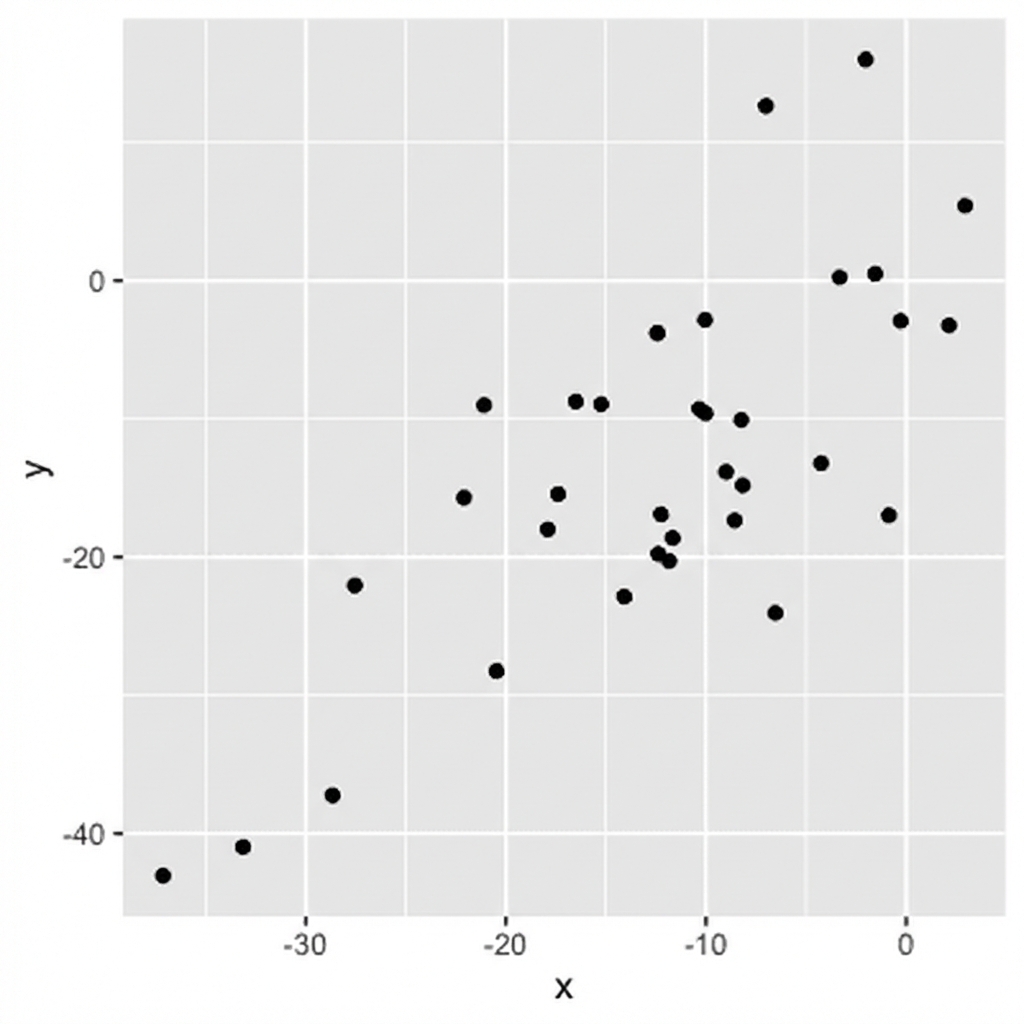
Ausmaß = Stärke der Beziehung
0,56 (mäßige Korrelation)
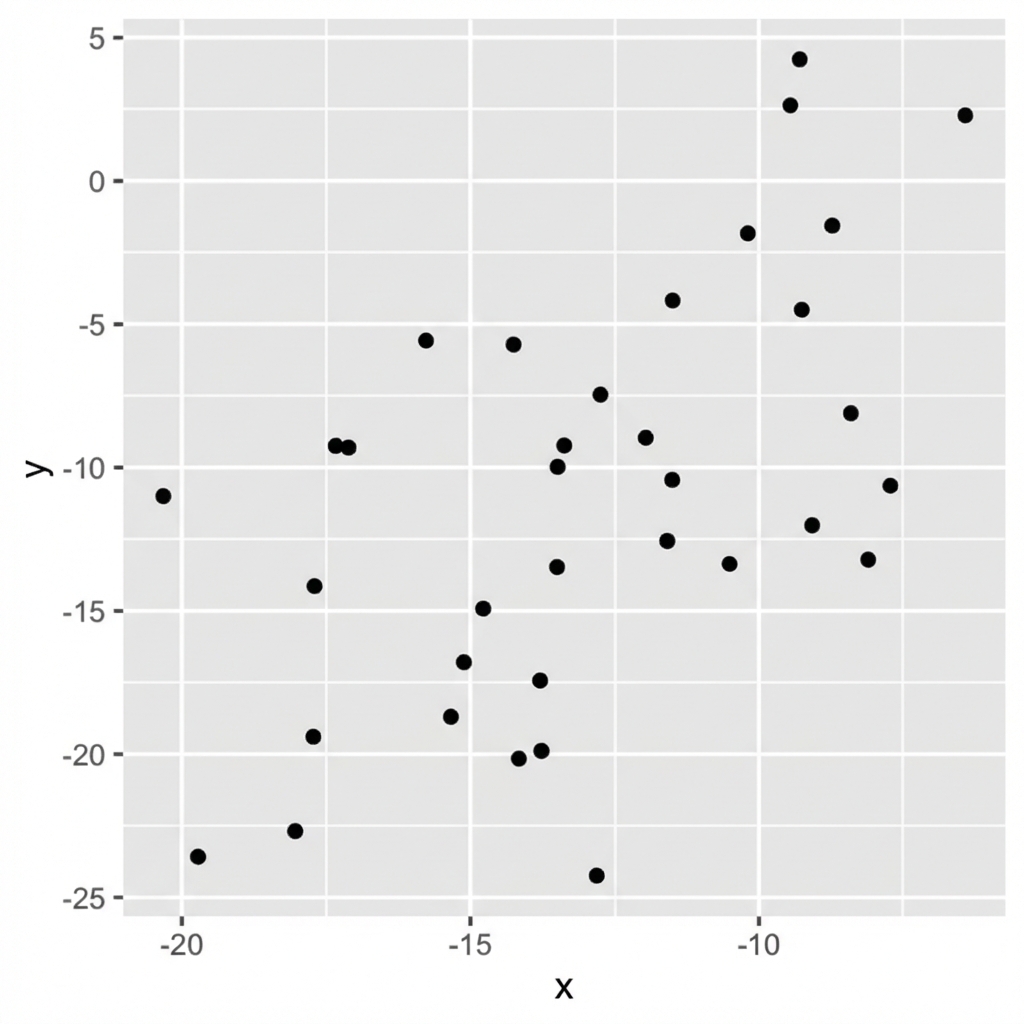
Ausmaß = Stärke der Beziehung
0,56 (mäßige Korrelation)

0,21 (schwache Korrelation)
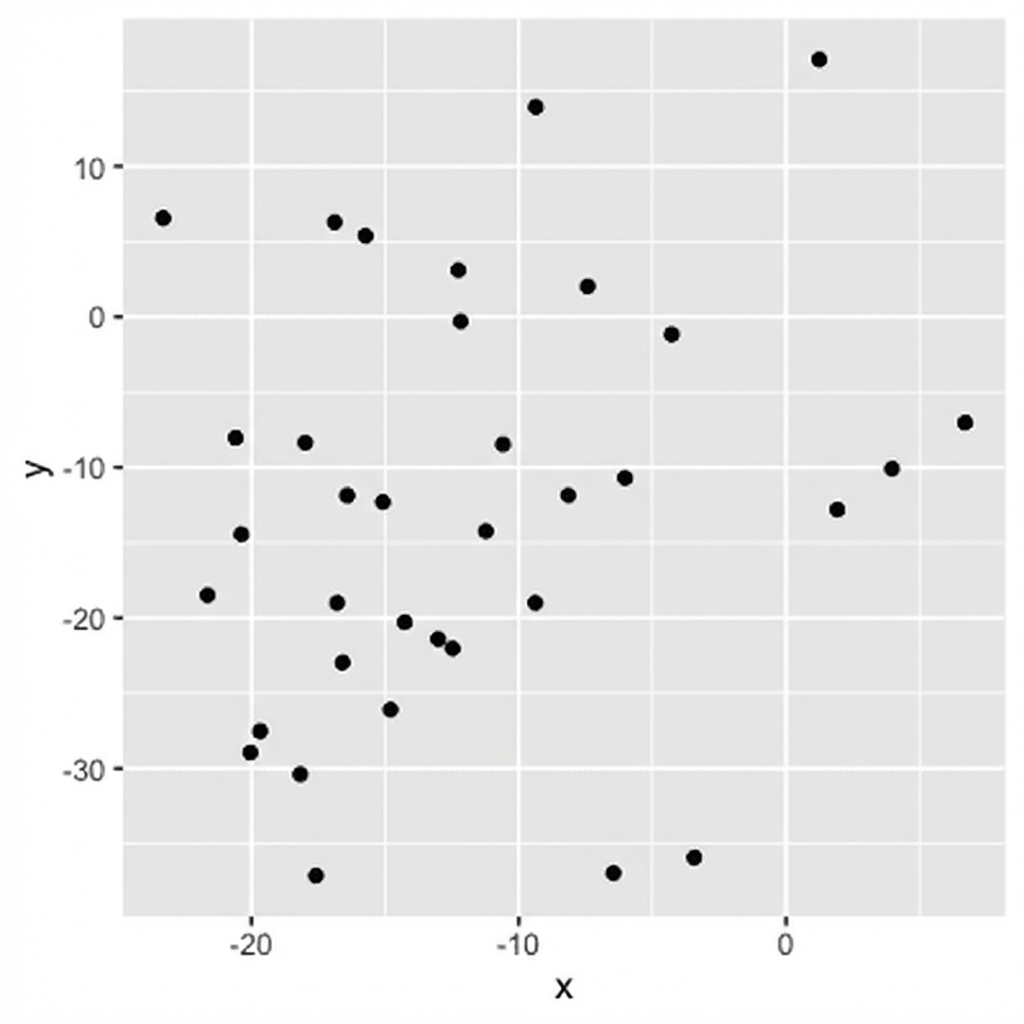
Ausmaß = Stärke der Beziehung
0,04 (keine Korrelation)
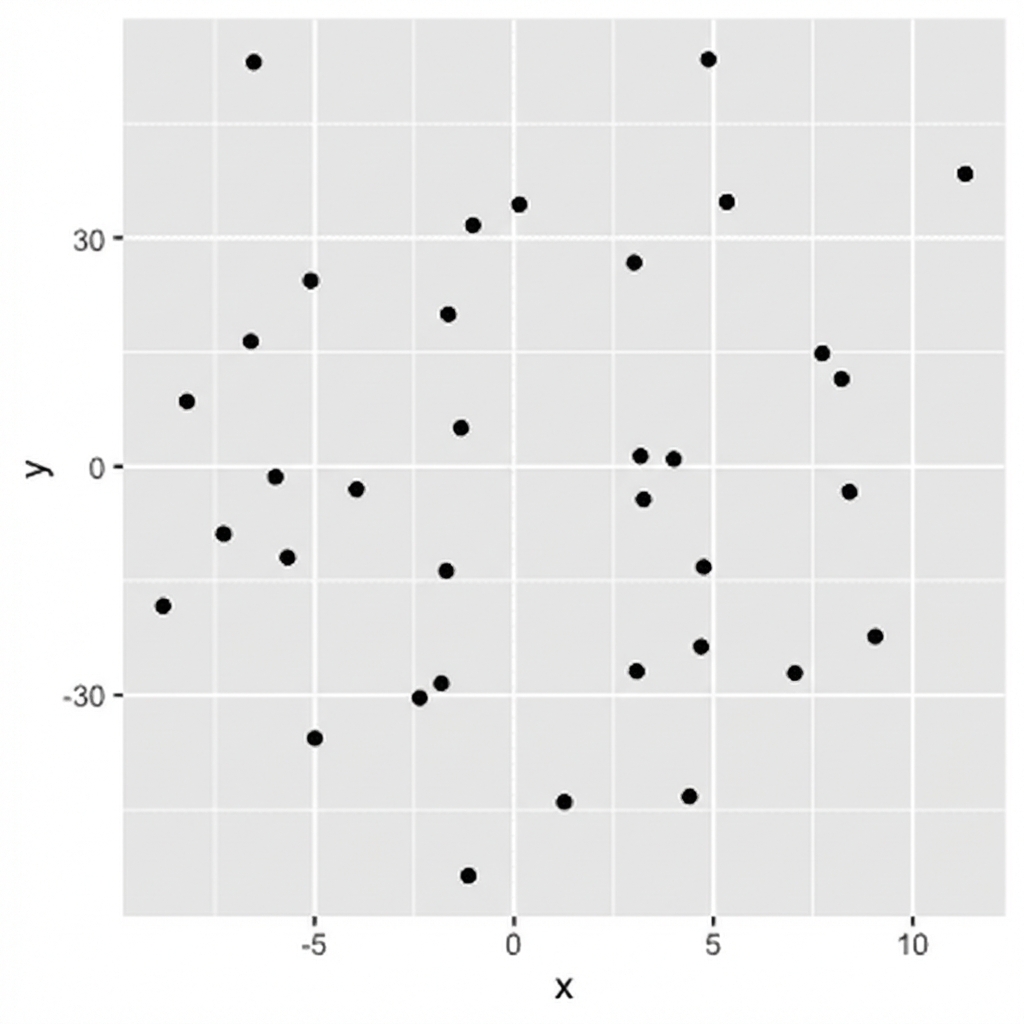
- Die Kenntnis des Wertes von
xsagt uns nichts überyaus
Vorzeichen = Richtung
0,75: Wenn x steigt, steigt y

-0,75: Wenn x steigt, sinkt y
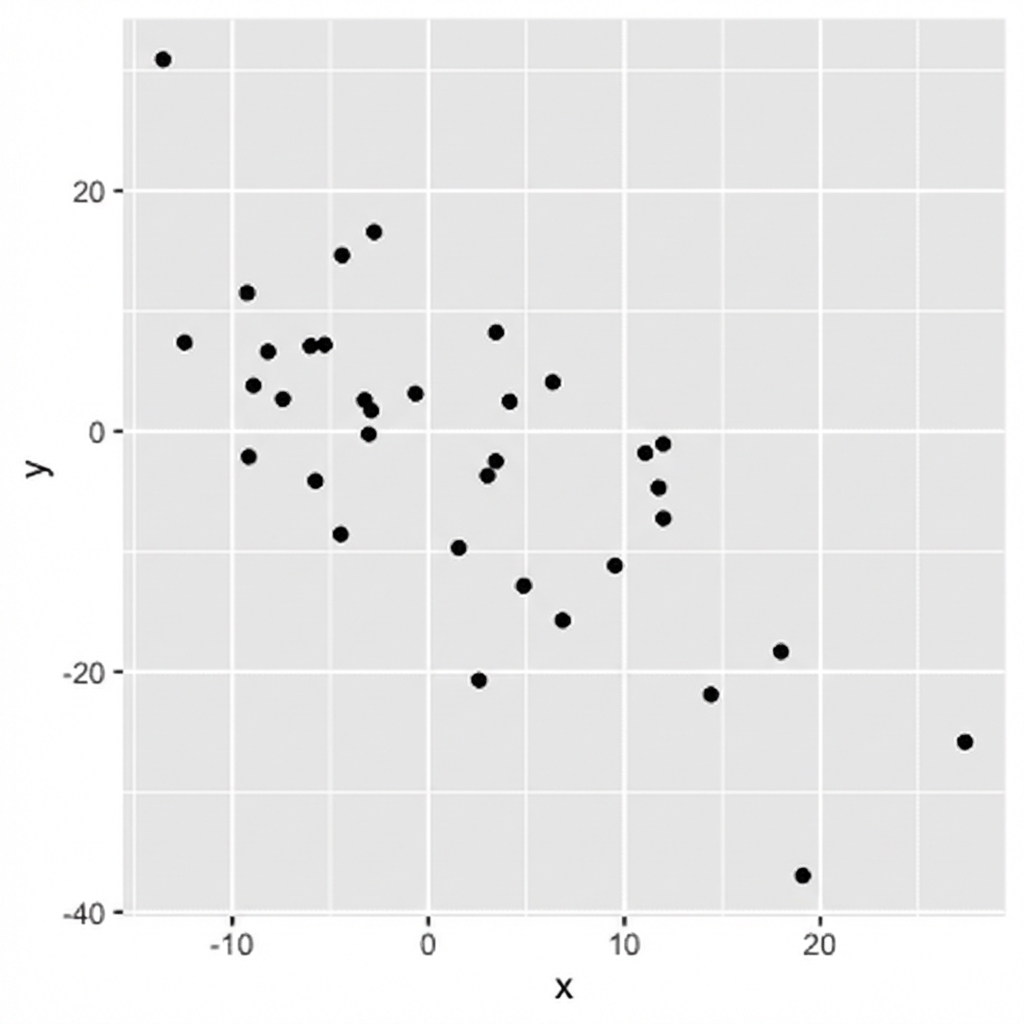
Beziehungen visualisieren
ggplot(df, aes(x, y)) +
geom_point()

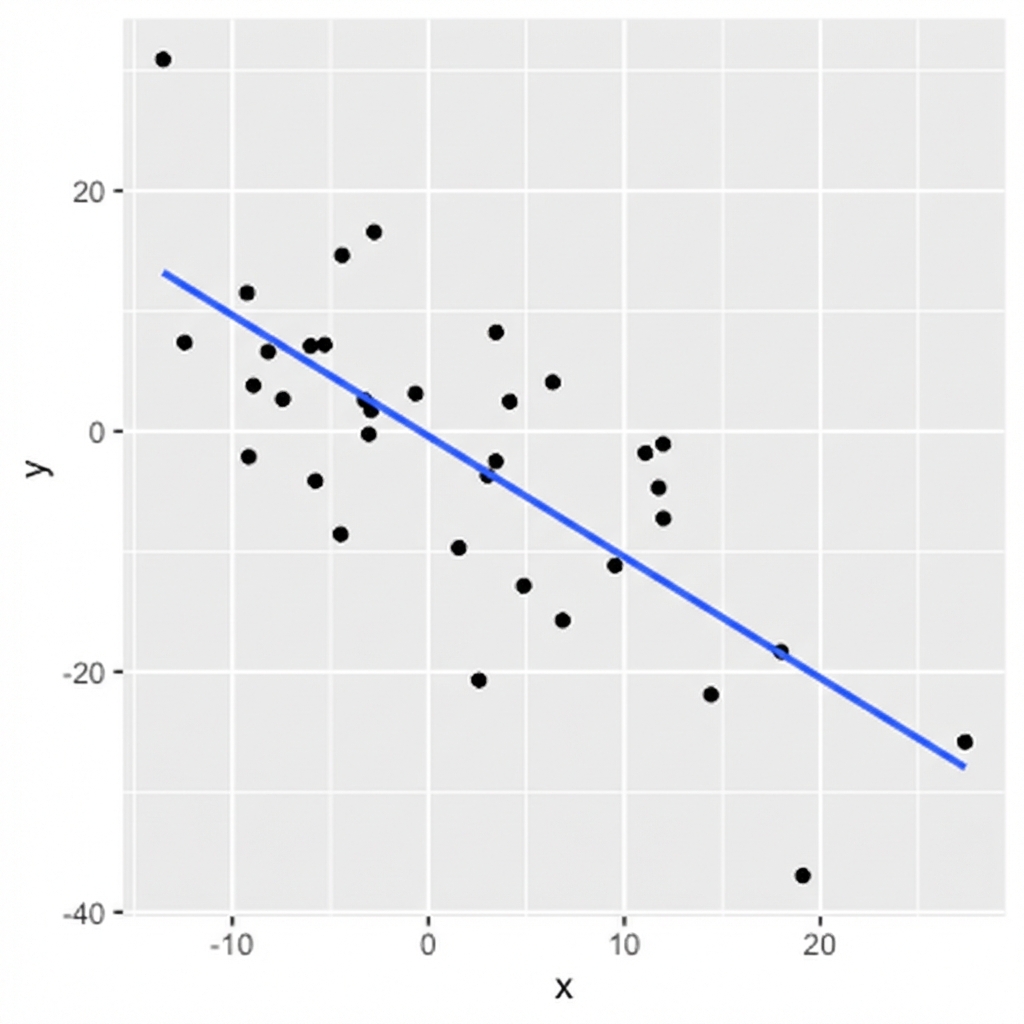
Hinzufügen einer Trendlinie
ggplot(df, aes(x, y)) + geom_point() +geom_smooth(method = "lm", se = FALSE)
Berechnung der Korrelation
cor(df$x, df$y)
-0.7472765
cor(df$y, df$x)
-0.7472765
Zusammenhang mit fehlenden Werten
df$x
-3.2508382 -9.1599807 3.4515013 4.1505899 NA 11.9806140 ...
cor(df$x, df$y)
NA
cor(df$x, df$y, use = "pairwise.complete.obs")
-0.7471757
Viele Wege zur Berechnung der Korrelation
- In diesem Kurs verwendet: Pearson Produkt-Moment-Korrelation ($r$)
- Am häufigsten verwendet
- $\bar{x} =$ Mittelwert von $x$
$$ r =\frac{\sum ^n _{i=1}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum ^n _{i=1}(x_i - \bar{x})^2} \sqrt{\sum ^n _{i=1}(y_i - \bar{y})^2}} $$
- Varianten dieser Formel:
- Kendall's Tau
- Spearman’sche Rangkorrelationskoeffizient
Lass uns üben!
Einführung in die Statistik in R

