Maße der Streuung

Einführung in die Statistik in R

Maggie Matsui

Content Developer, DataCamp

Was ist Streuung?

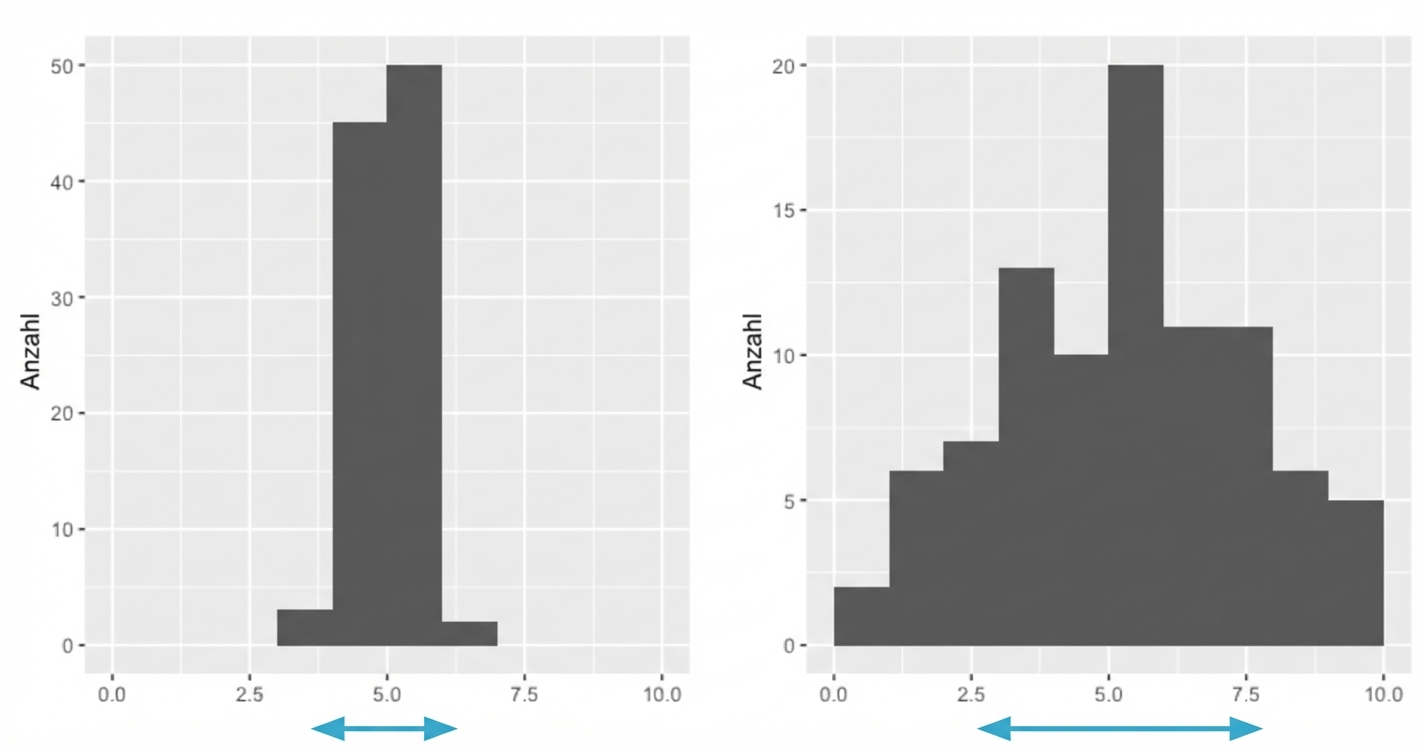
Zwei Histogramme: ein schmales mit Daten, die nur wenige Werte umfassen, und ein breiteres mit Daten, die mehr Werte umfassen

Varianz

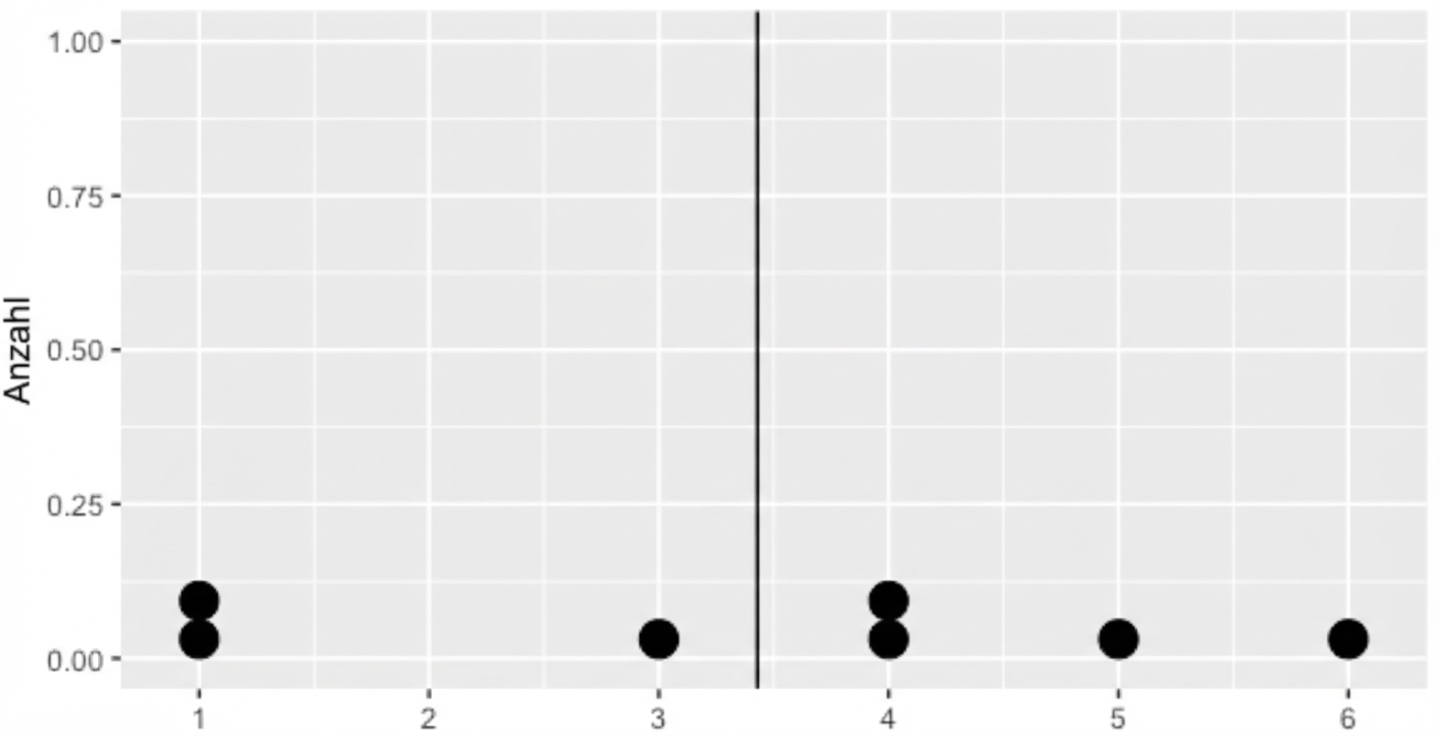
Durchschnittlicher Abstand von jedem Datenpunkt zum Mittelwert der Daten Ein Punktdiagramm mit 7 Datenpunkten und einer schwarzen Linie in der Mitte, die den Mittelwert darstellt.

Die Varianz berechnen

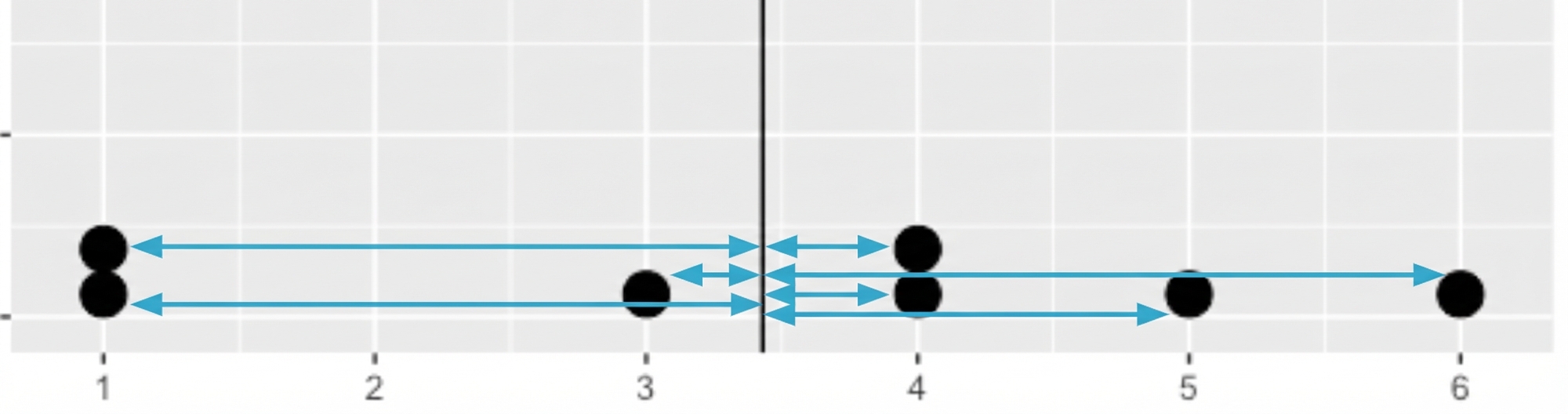
Ein Punktdiagramm mit 7 Datenpunkten und einer schwarzen Linie in der Mitte, die den Mittelwert darstellt. Zwischen jedem Punkt und der Mittellinie sind Pfeile.

dists <- msleep$sleep_total - mean(msleep$sleep_total)
dists

1.66626506  6.56626506 ... -4.13373494  2.06626506 -0.63373494

Die Varianz berechnen

squared_dists <- (dists)^2

2.776439251 43.115836841 ... 17.087764552  4.269451299  0.401619974

sum_sq_dists <- sum(squared_dists)
sum_sq_dists

1624.066

Die Varianz berechnen

sum_sq_dists/82

19.80568

var(msleep$sleep_total)

19.80568

Standardabweichung

sqrt(var(msleep$sleep_total))

4.450357

# Standard deviation of 'sleep_total'
sd(msleep$sleep_total)

4.450357

Mittlere absolute Abweichung

dists <- msleep$sleep_total - mean(msleep$sleep_total)
mean(abs(dists))

3.566701

Standardabweichung vs. mittlere absolute Abweichung

Die Standardabweichung quadriert Abstände und bestraft längere Strecken stärker als kürzere.
Die mittlere absolute Abweichung bestraft jeden Abstand gleich.
Das eine ist nicht besser als das andere, aber die Standardabweichung kommt häufiger vor als die mittlere absolute Abweichung.

Quartile

quantile(msleep$sleep_total)

   0%   25%   50%   75%  100% 
 1.90  7.85 10.10 13.75 19.90

Zweites Quartil/50. Perzentil = Median

Kastendiagramme verwenden Quartile

ggplot(msleep, aes(y = sleep_total)) +
  geom_boxplot()

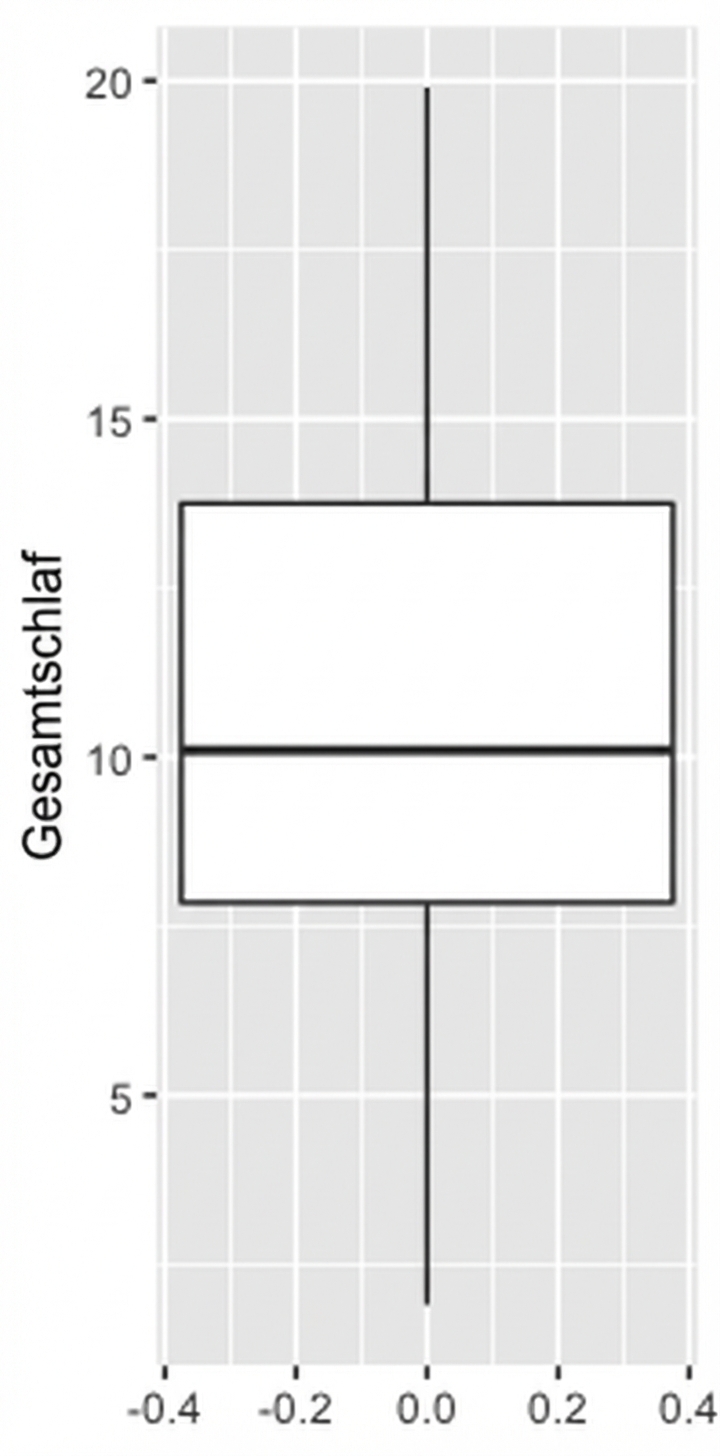
Ein Boxplot der Gesamtschlafzeit von Säugetieren

Quantile

quantile(msleep$sleep_total, probs = c(0, 0.2, 0.4, 0.6, 0.8, 1))

   0%   20%   40%   60%   80%  100% 
 1.90  6.24  9.48 11.14 14.40 19.90

seq(from, to, by)

quantile(msleep$sleep_total, probs = seq(0, 1, 0.2))

   0%   20%   40%   60%   80%  100% 
 1.90  6.24  9.48 11.14 14.40 19.90

Interquartilsabstand (IQR)

Höhe des Kastens in einem Kastendiagramm

iqr = quantile(msleep$sleep_total, 0.75) - quantile(msleep$sleep_total, 0.25)
iqr

75%
5.9

Ausreißer

Ausreißer: Datenpunkt, der sich wesentlich von den anderen unterscheidet

Woher wissen wir, was ein wesentlicher Unterschied ist? Ein Datenpunkt ist ein Ausreißer, wenn:

$\text{data} < \text{Q1} - 1.5\times\text{IQR}$ oder
$\text{Datenpunkt} > \text{Q3} + 1,5\times\text{IQR}$

Ausreißer finden

iqr <- quantile(msleep$bodywt, 0.75) - quantile(msleep$bodywt, 0.25)

lower_threshold <- quantile(msleep$bodywt, 0.25) - 1.5 * iqr
upper_threshold<- quantile(msleep$bodywt, 0.75) + 1.5 * iqr

msleep %>% filter(bodywt < lower_threshold | bodywt > upper_threshold ) %>% 
  select(name, vore, sleep_total, bodywt)

# A tibble: 11 x 4
   name                 vore  sleep_total bodywt
   <chr>                <chr>       <dbl>  <dbl> 
 1 Cow                  herbi         4      600 
 2 Asian elephant       herbi         3.9   2547 
 3 Horse                herbi         2.9    521 
 ...

Lass uns üben!

Einführung in die Statistik in R