Kontinuierliche Verteilungen
Einführung in die Statistik in R
Maggie Matsui
Content Developer, DataCamp
Warten auf den Bus
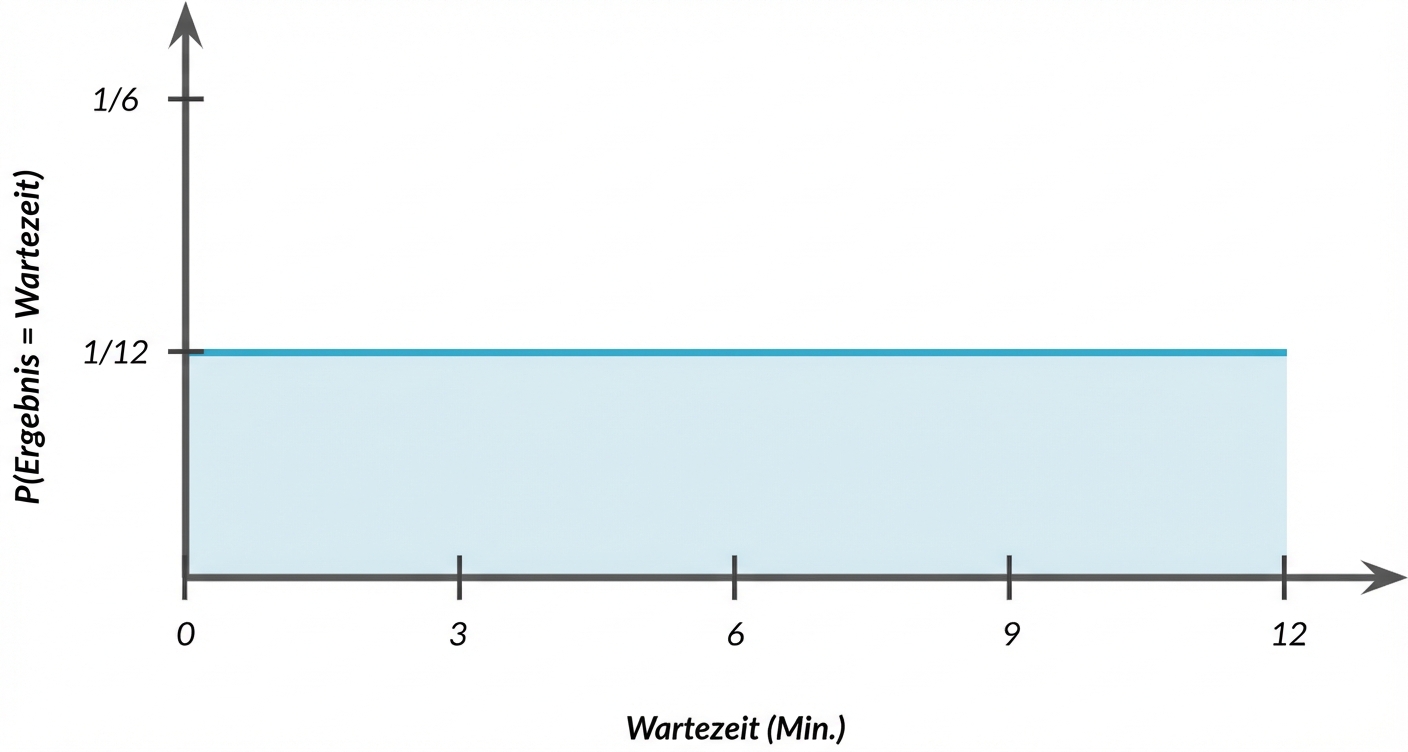
Kontinuierliche Gleichverteilung
Kontinuierliche Gleichverteilung
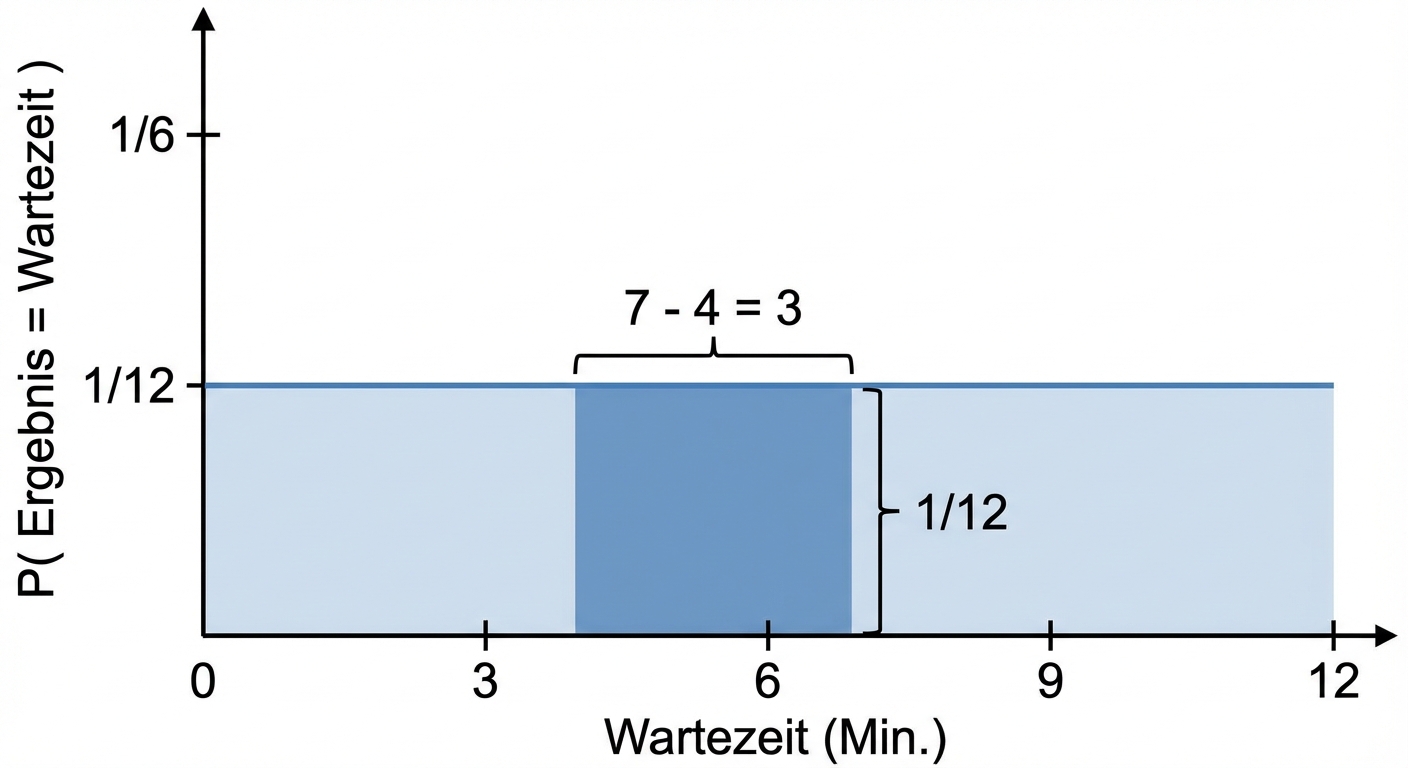
Wahrscheinlichkeit = Fläche
$$P(4 \le \text{wait time} \le 7) = ~~ ?$$
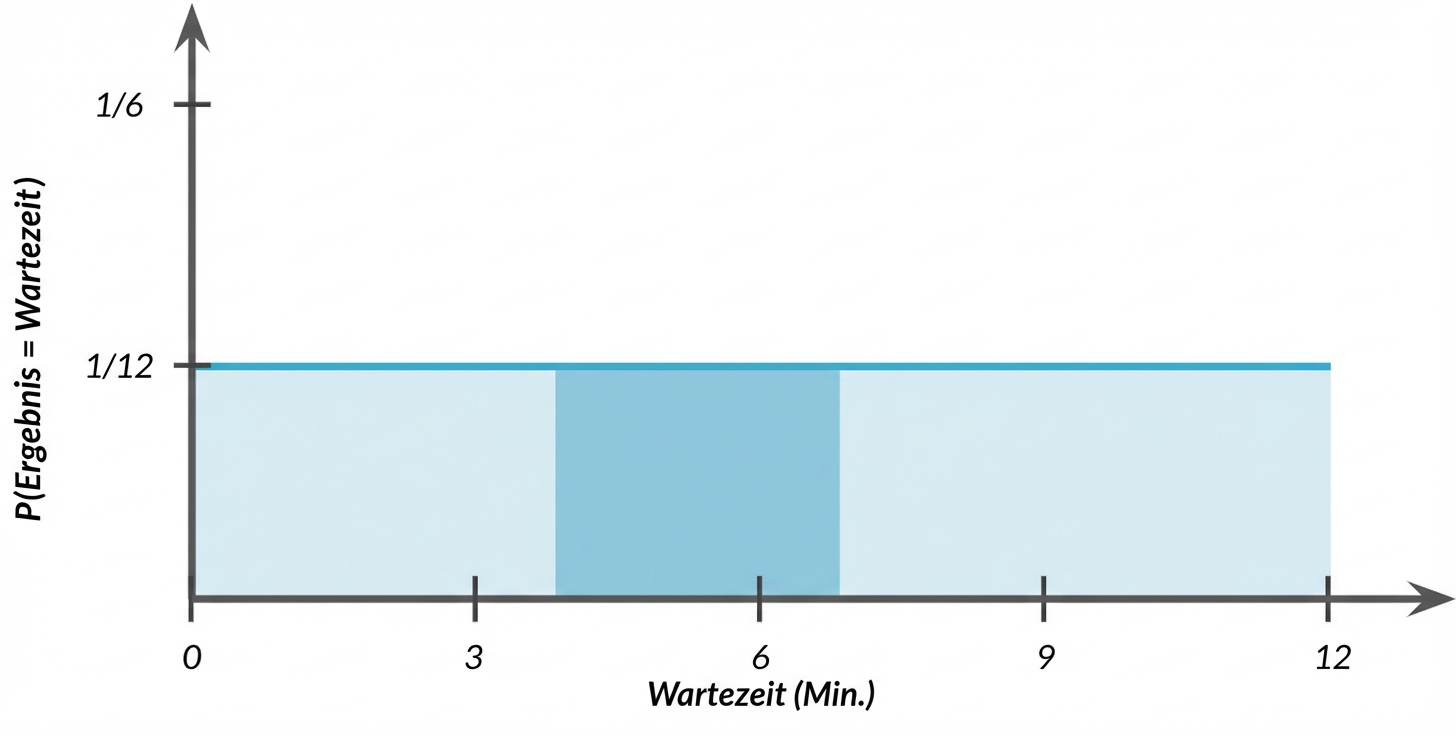
Wahrscheinlichkeit = Fläche
$$P(4 \le \text{wait time} \le 7) = ~~ ?$$
Wahrscheinlichkeit = Fläche
$$P(4 \le \text{wait time} \le 7) = 3 \times 1/12 = 3/12$$
Gleichmäßige Verteilung in R
$$ P(\text{wait time} \le 7)$$
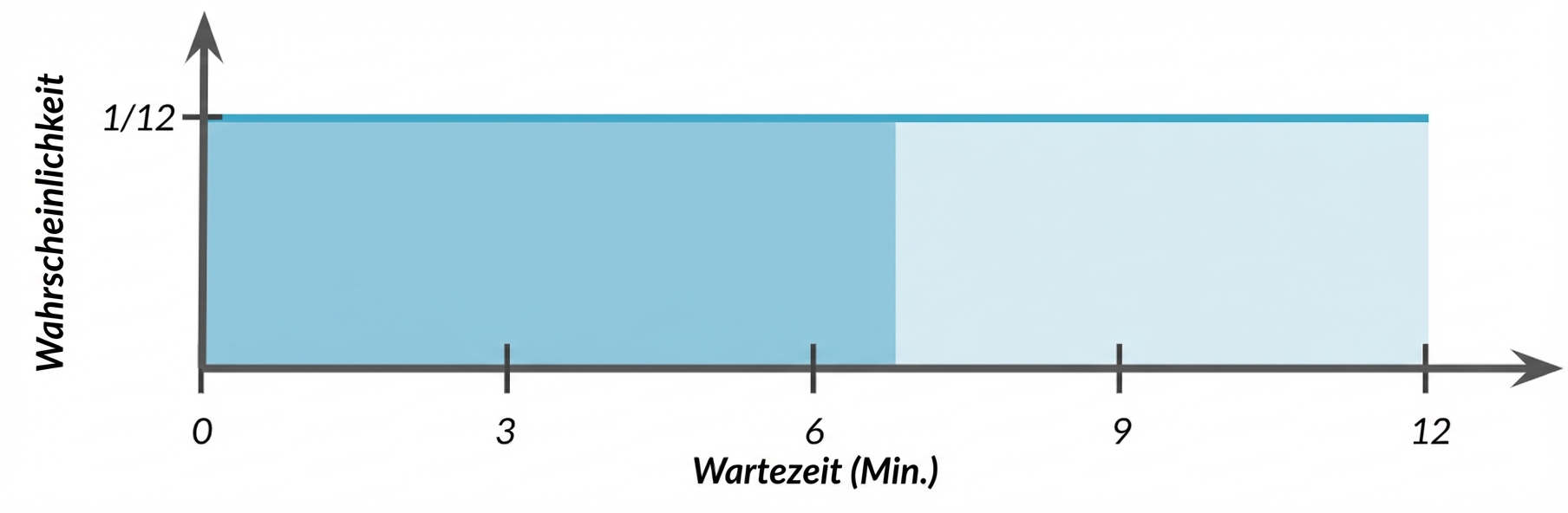
punif(7, min = 0, max = 12)
0.5833333
lower.tail
$$ P(\text{wait time} \ge 7)$$
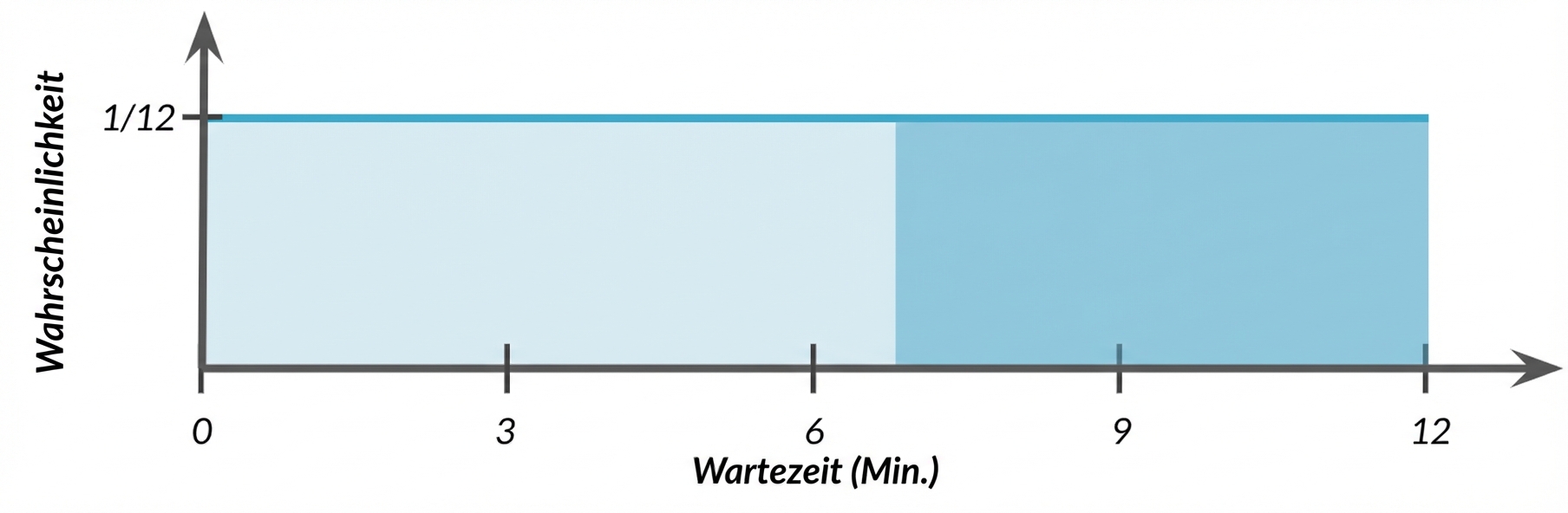
punif(7, min = 0, max = 12, lower.tail = FALSE)
0.4166667
$$ P(4 \le \text{wait time} \le 7)$$
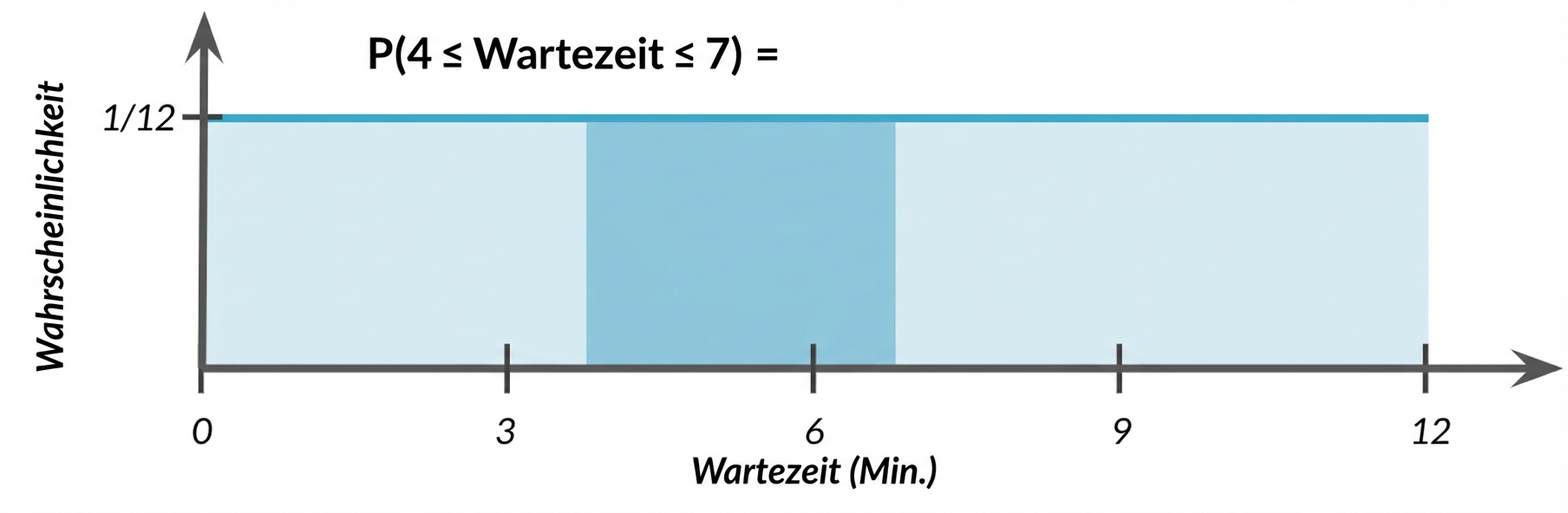
$$ P(4 \le \text{wait time} \le 7)$$
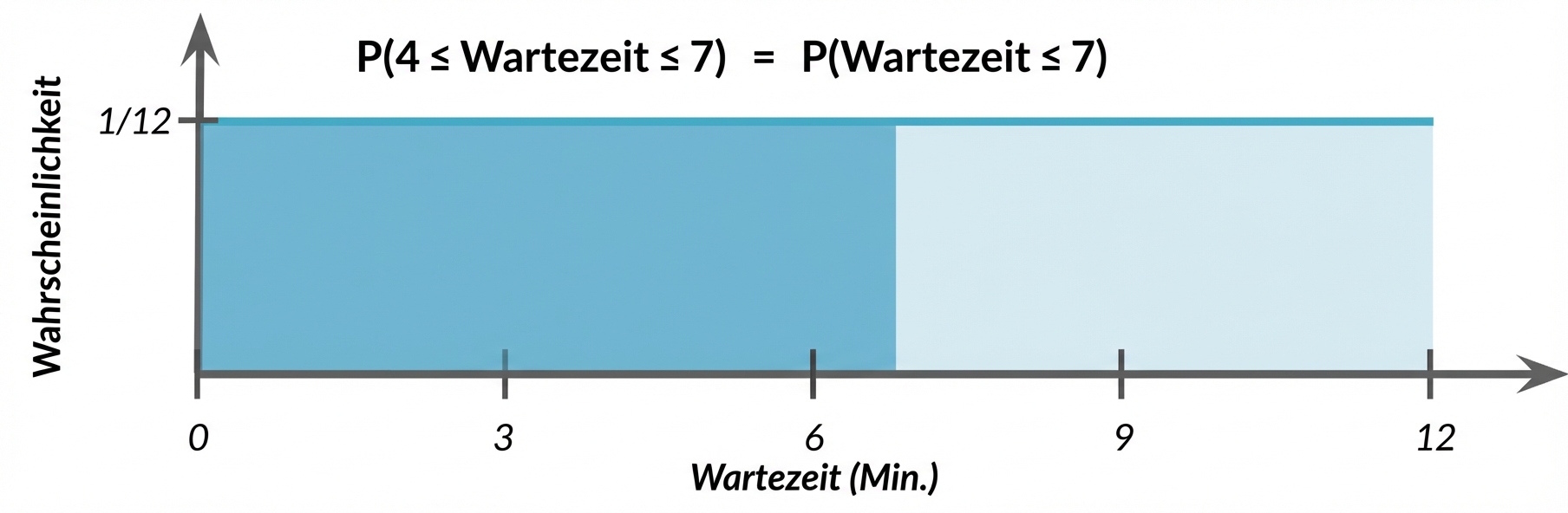
$$ P(4 \le \text{wait time} \le 7)$$
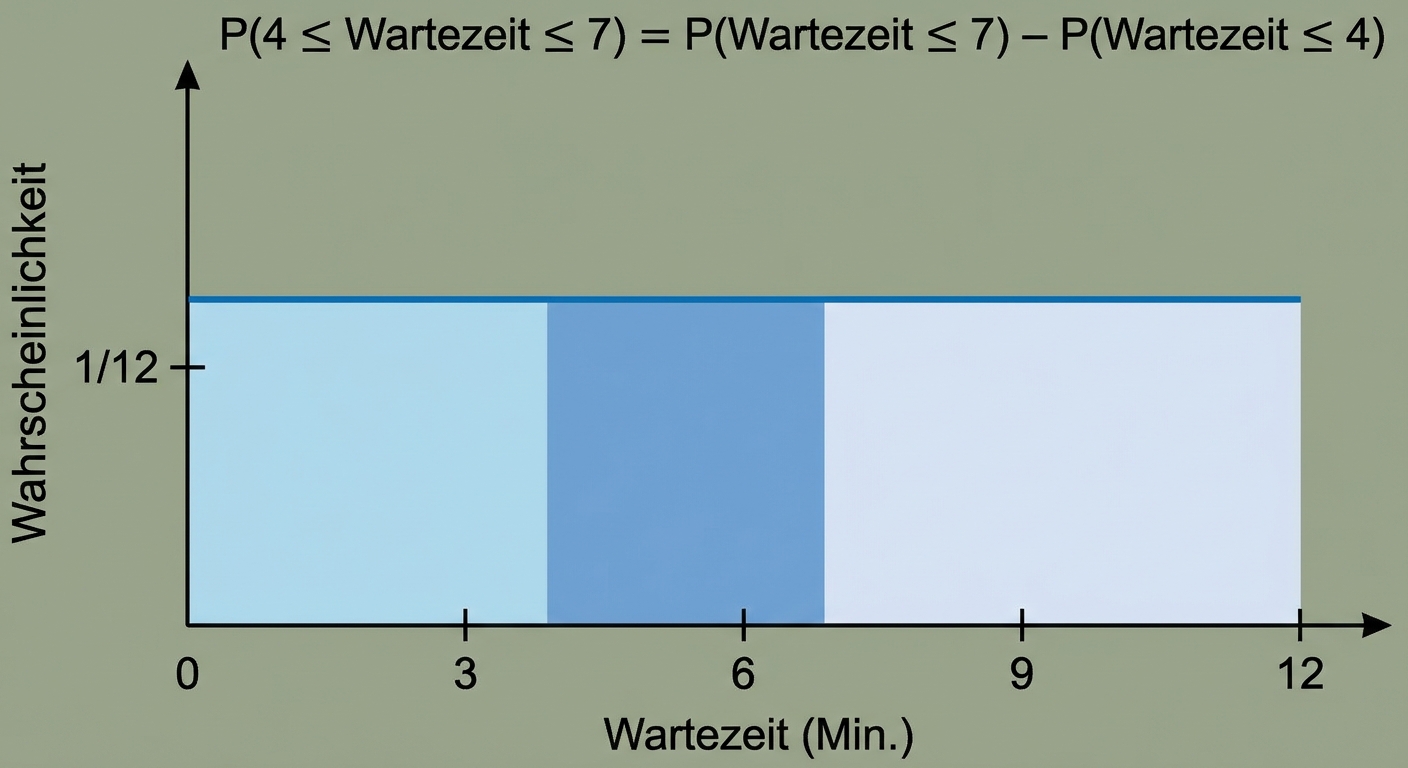
punif(7, min = 0, max = 12) - punif(4, min = 0, max = 12)
0.25
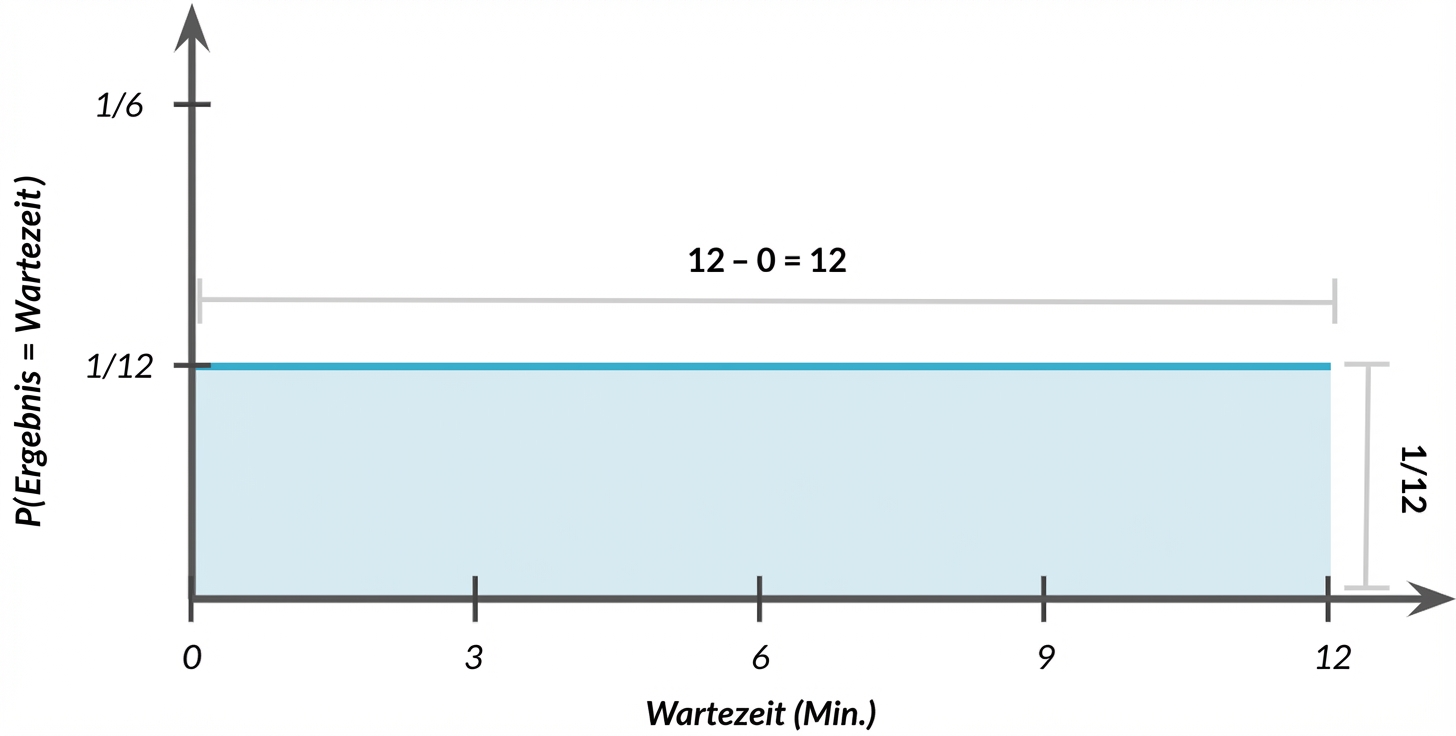
Gesamtfläche = 1
$$P(0 \le \text{wait time} \le 12) = ~~ ?$$
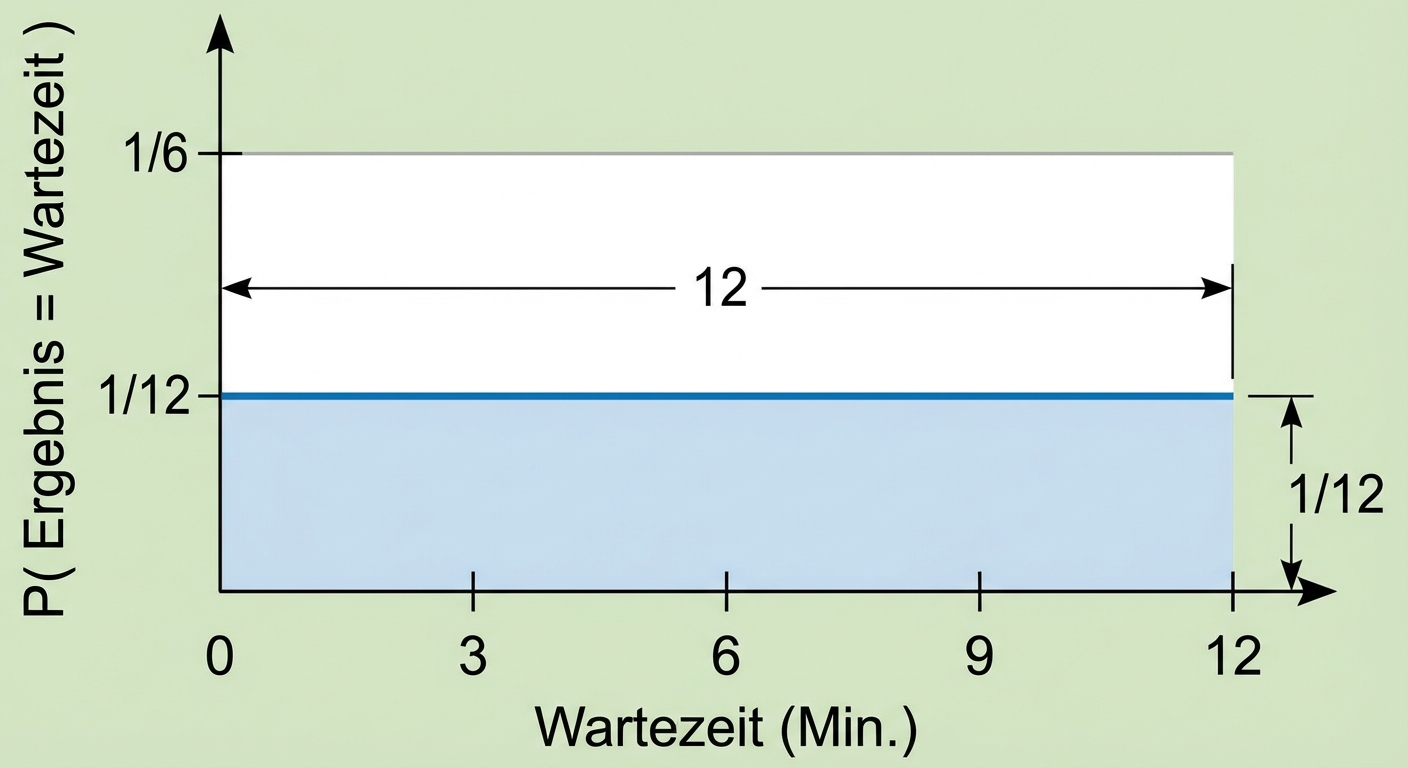
Gesamtfläche = 1
$$P(0 \le \text{outcome} \le 12) = 12 \times 1/12 = 1$$
Andere kontinuierliche Verteilungen
Andere kontinuierliche Verteilungen
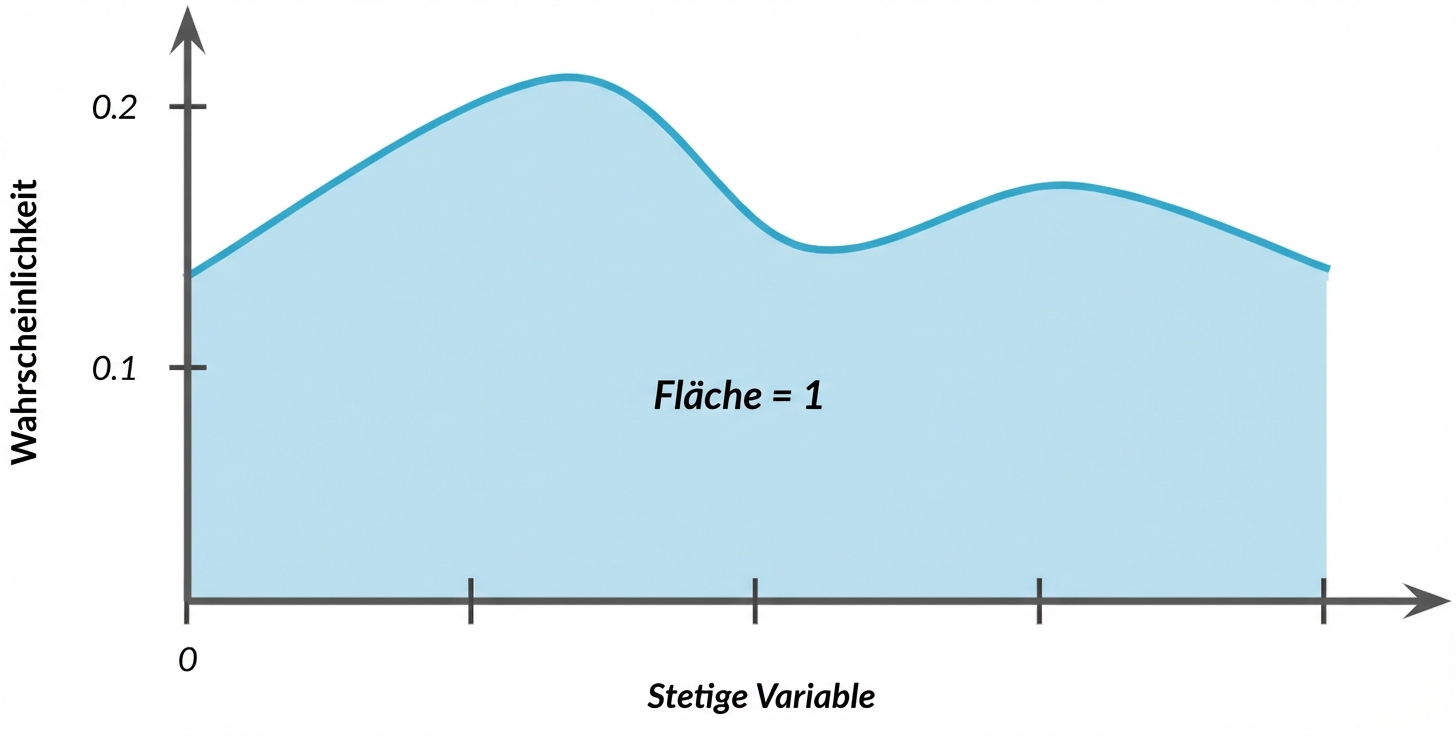
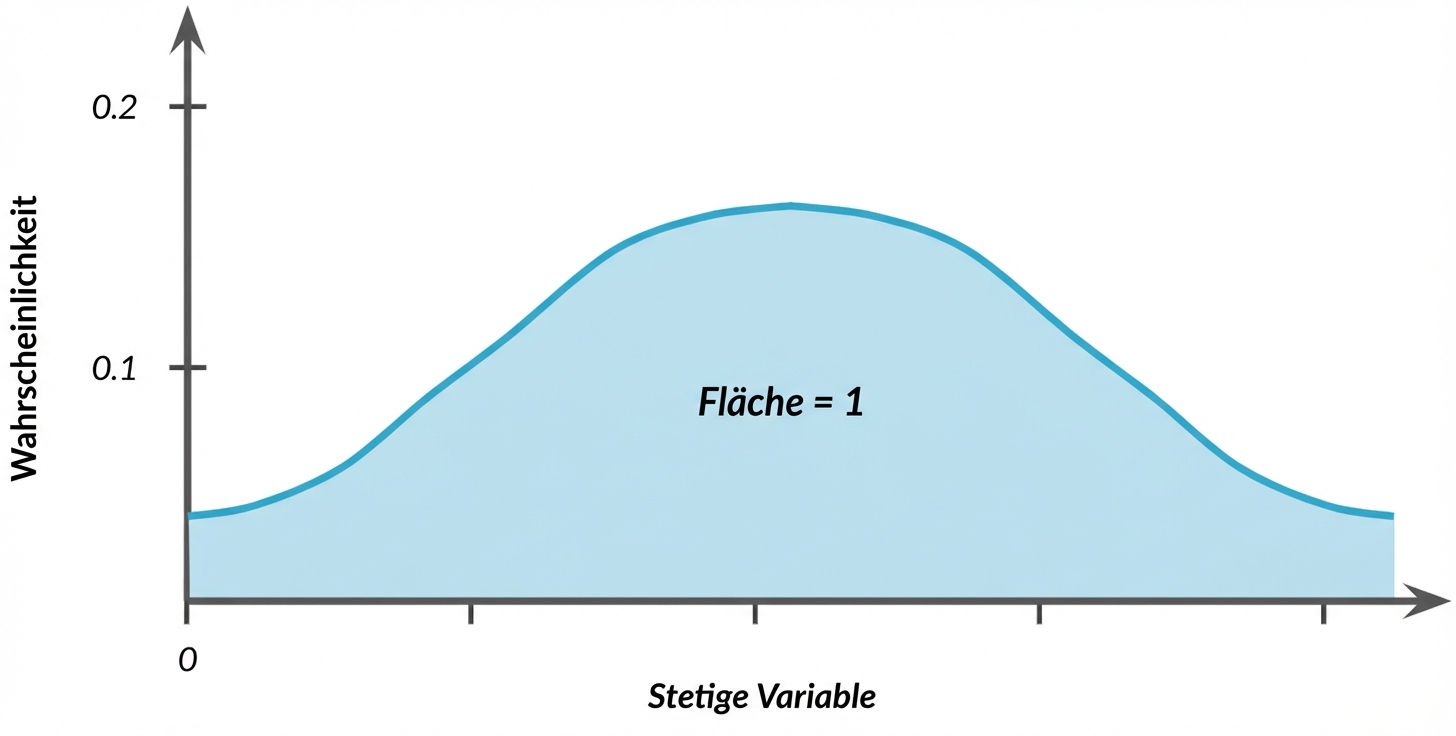
Andere besondere Arten von Verteilungen
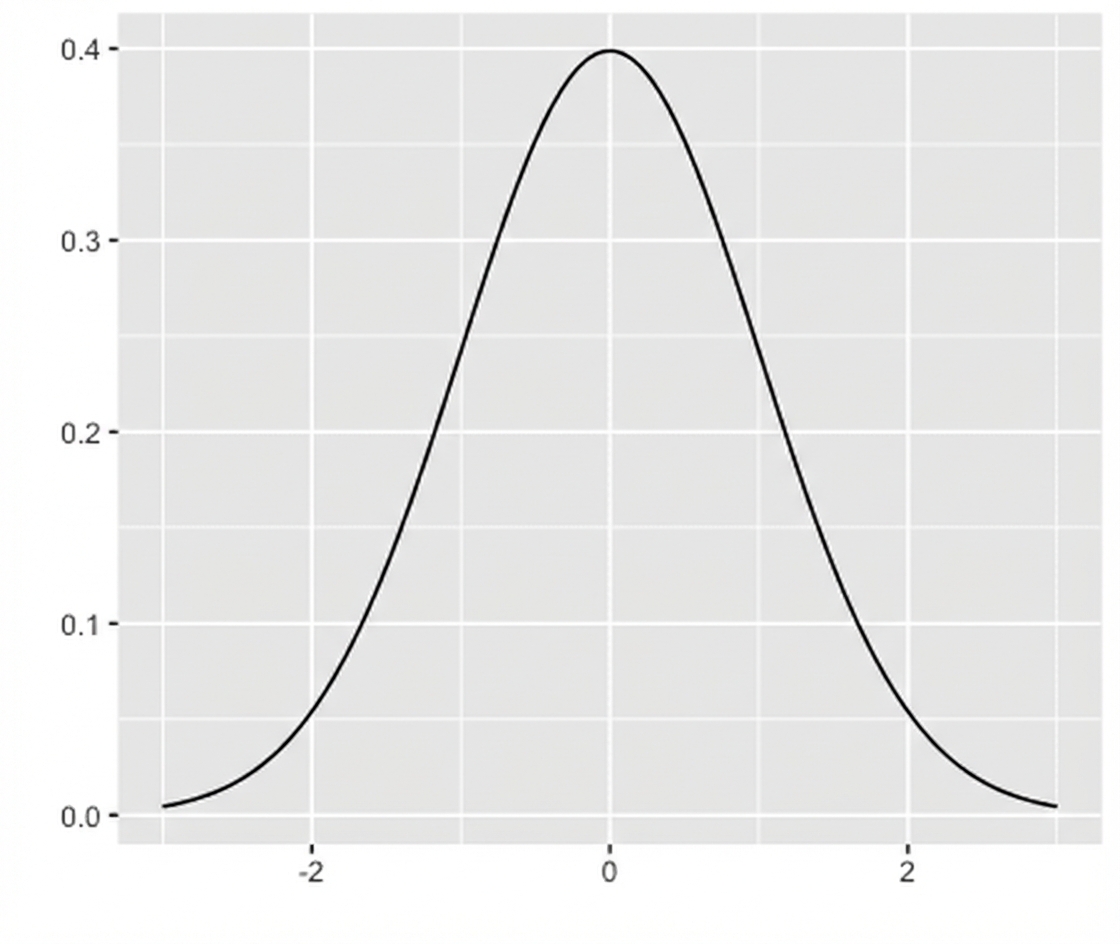
Normalverteilung
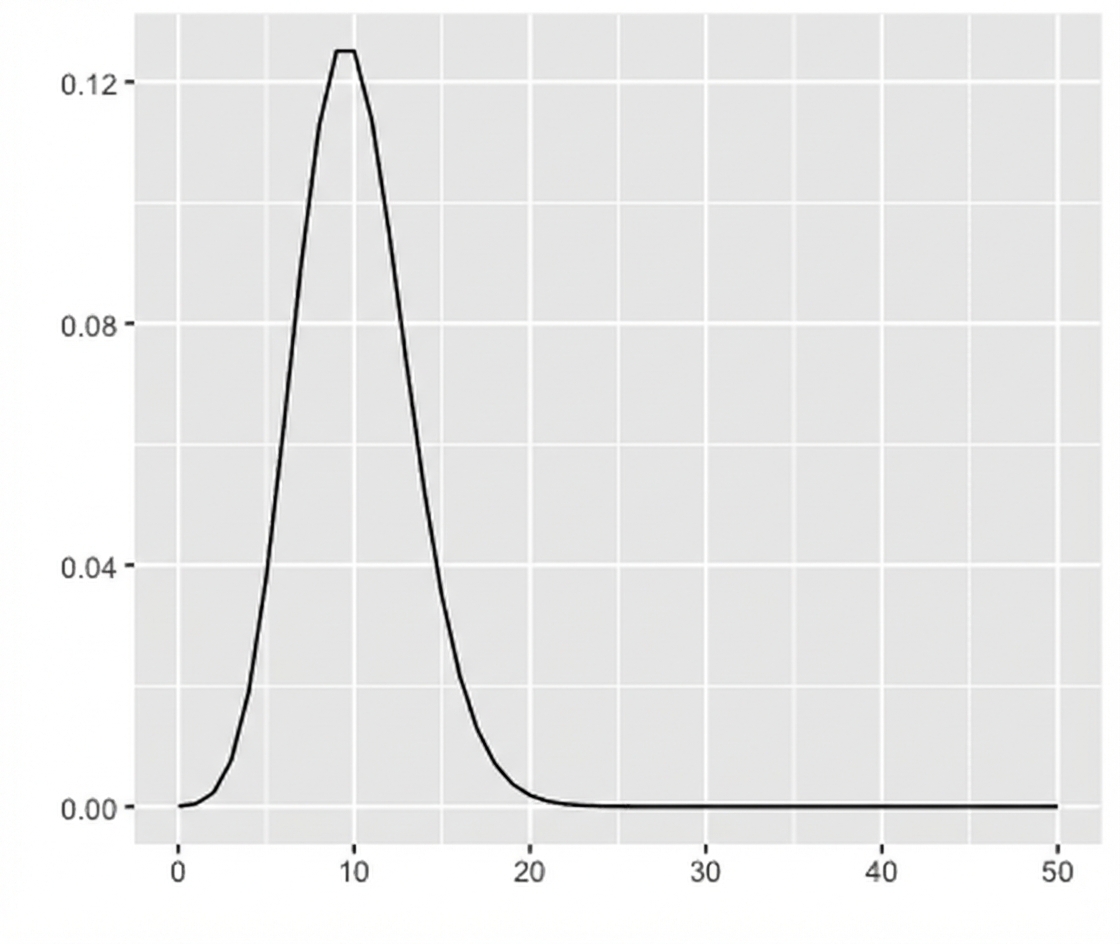
Poisson-Verteilung
