Die Poisson-Verteilung

Einführung in die Statistik in R

Maggie Matsui

Content Developer, DataCamp

Poisson-Prozesse

Ereignisse scheinen in einem bestimmten Rhythmus zu passieren, aber völlig zufällig
Beispiele
- Anzahl der Tiere, die pro Woche aus einem Tierheim adoptiert werden
- Anzahl der Personen, die pro Stunde ein Restaurant betreten
- Anzahl der Erdbeben in Kalifornien pro Jahr

Hund im Tierheim mit Familie

Die Wahrscheinlichkeit, dass eine bestimmte Anzahl von Ereignissen innerhalb eines bestimmten Zeitraums eintritt
Beispiele
- Wahrscheinlichkeit, dass $\ge$ 5 Tiere pro Woche aus einem Tierheim adoptiert werden
- Wahrscheinlichkeit, dass 12 Personen pro Stunde ein Restaurant betreten
- Wahrscheinlichkeit von $\lt$ 20 Erdbeben in Kalifornien pro Jahr

$\lambda$ = durchschnittliche Anzahl von Ereignissen pro Zeitspanne
- Durchschnittliche Anzahl von Adoptionen pro Woche = 8

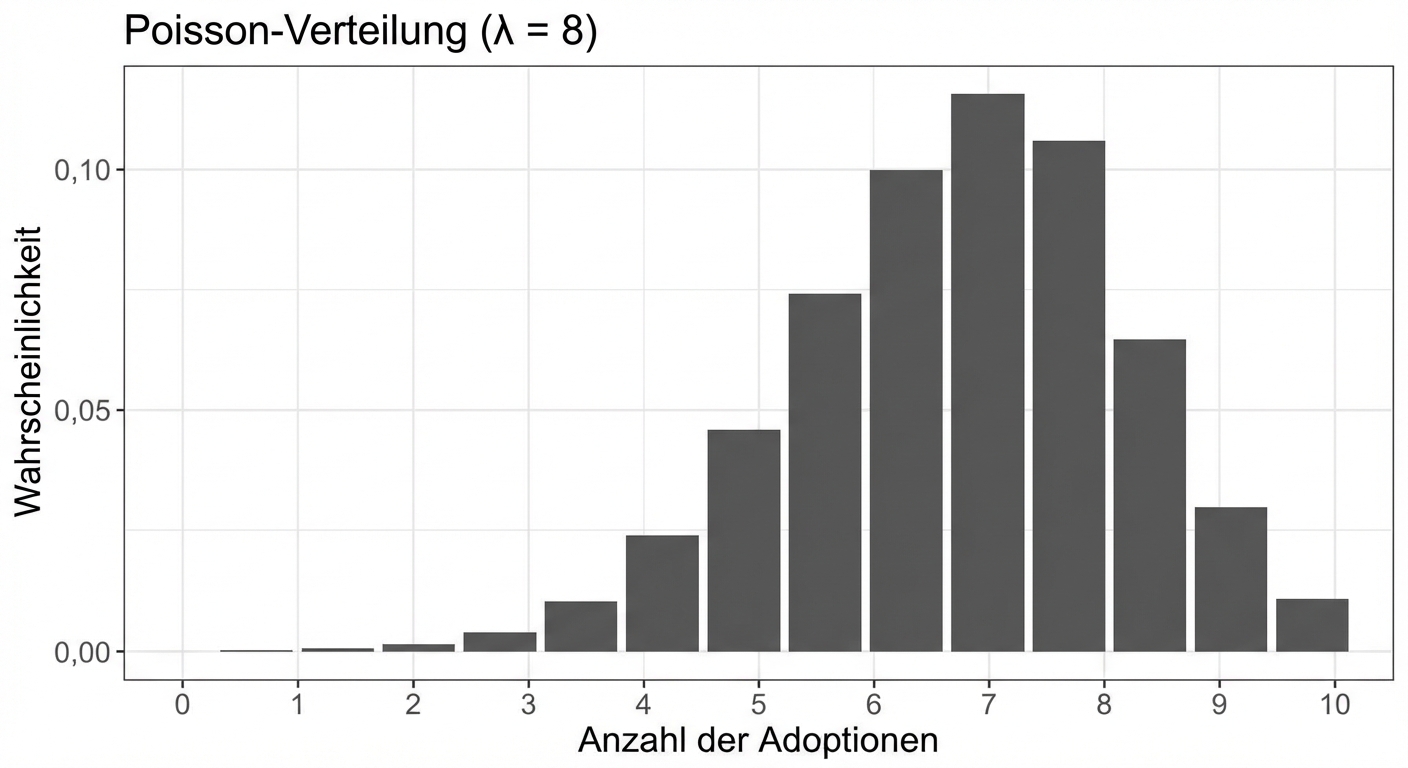
Poisson-Verteilung mit Lambda = 8

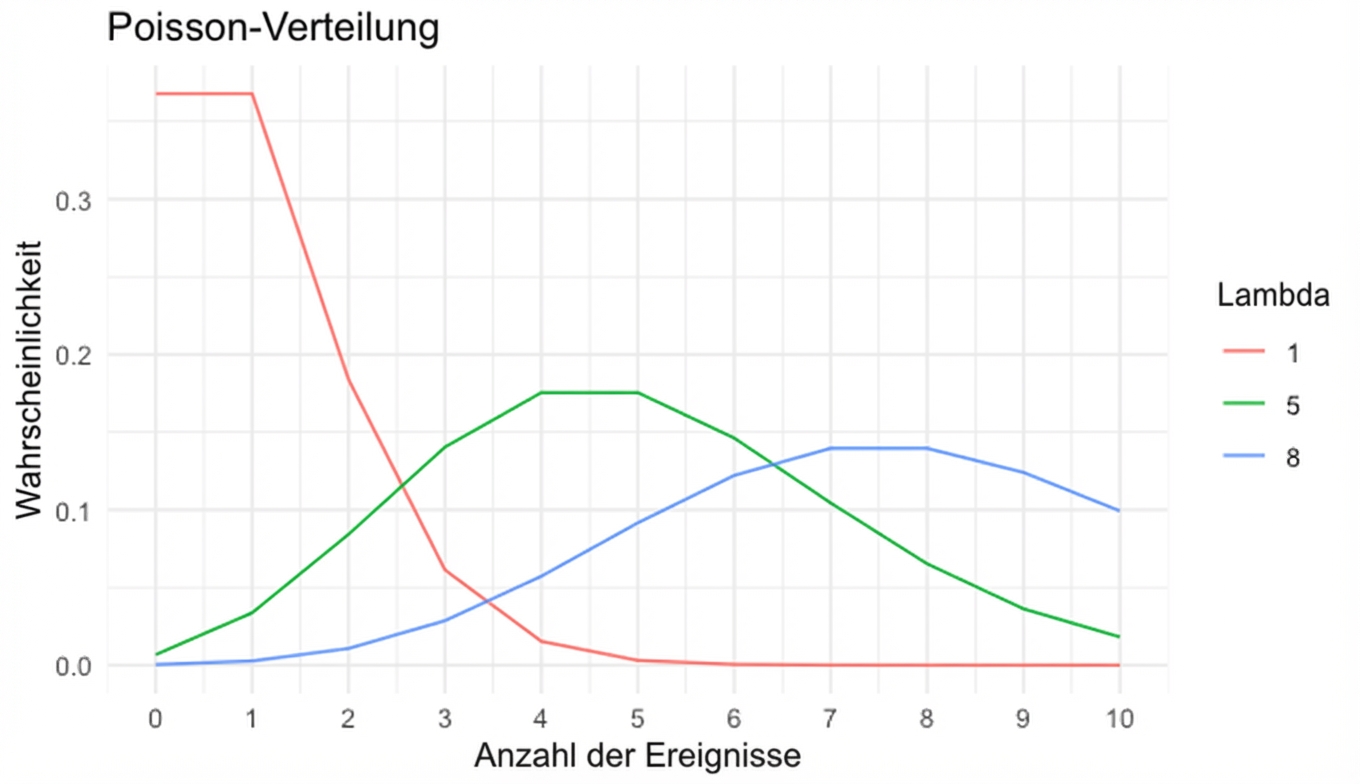
3 Poisson-Verteilungen: eine mit Lambda = 1, eine mit Lambda = 5 und eine mit Lambda = 8

Wenn die durchschnittliche Anzahl der Adoptionen pro Woche 8 beträgt, wie hoch ist dann $P(\text{# adoptions in a week} = 5)$?

dpois(5, lambda = 8)

0.09160366

Wenn die durchschnittliche Anzahl der Adoptionen pro Woche 8 beträgt, wie hoch ist dann $P(\text{# adoptions in a week} \le 5)$?

ppois(5, lambda = 8)

0.1912361

Wenn die durchschnittliche Anzahl der Adoptionen pro Woche 8 beträgt, wie hoch ist dann $P(\text{# adoptions in a week} \gt 5)$?

ppois(5, lambda = 8, lower.tail = FALSE)

0.8087639

Wenn die durchschnittliche Anzahl der Adoptionen pro Woche 10 beträgt, wie hoch ist dann $P(\text{# adoptions in a week} \gt 5)$?

ppois(5, lambda = 10, lower.tail = FALSE)

0.932914

rpois(10, lambda = 8)

13  6 11  7 10  8  7  3  7  6

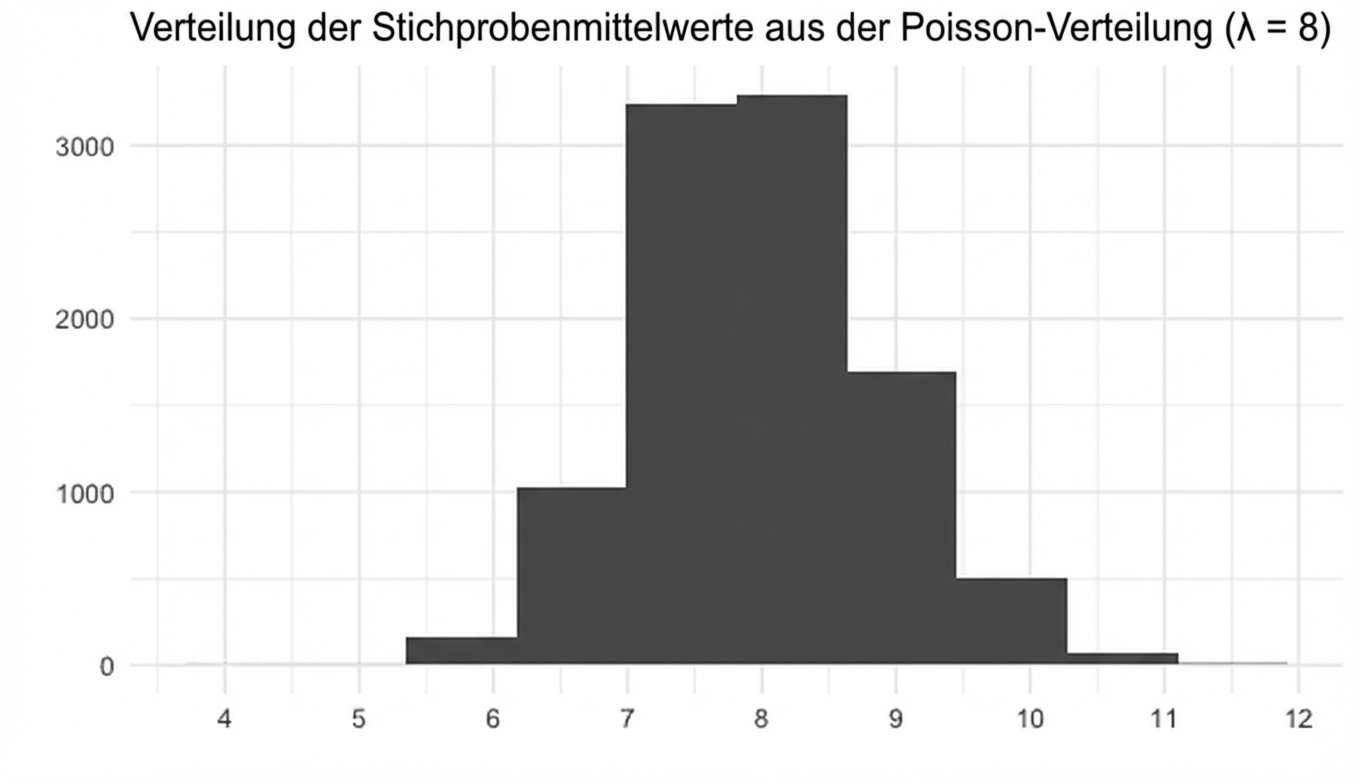
Verteilung der Stichprobenmittelwerte aus der Poisson-Verteilung mit Lambda = 8. Ähnelt der Normalverteilung

Einführung in die Statistik in R