Die Normalverteilung

Einführung in die Statistik in R

Maggie Matsui

Content Developer, DataCamp

Was ist die Normalverteilung?

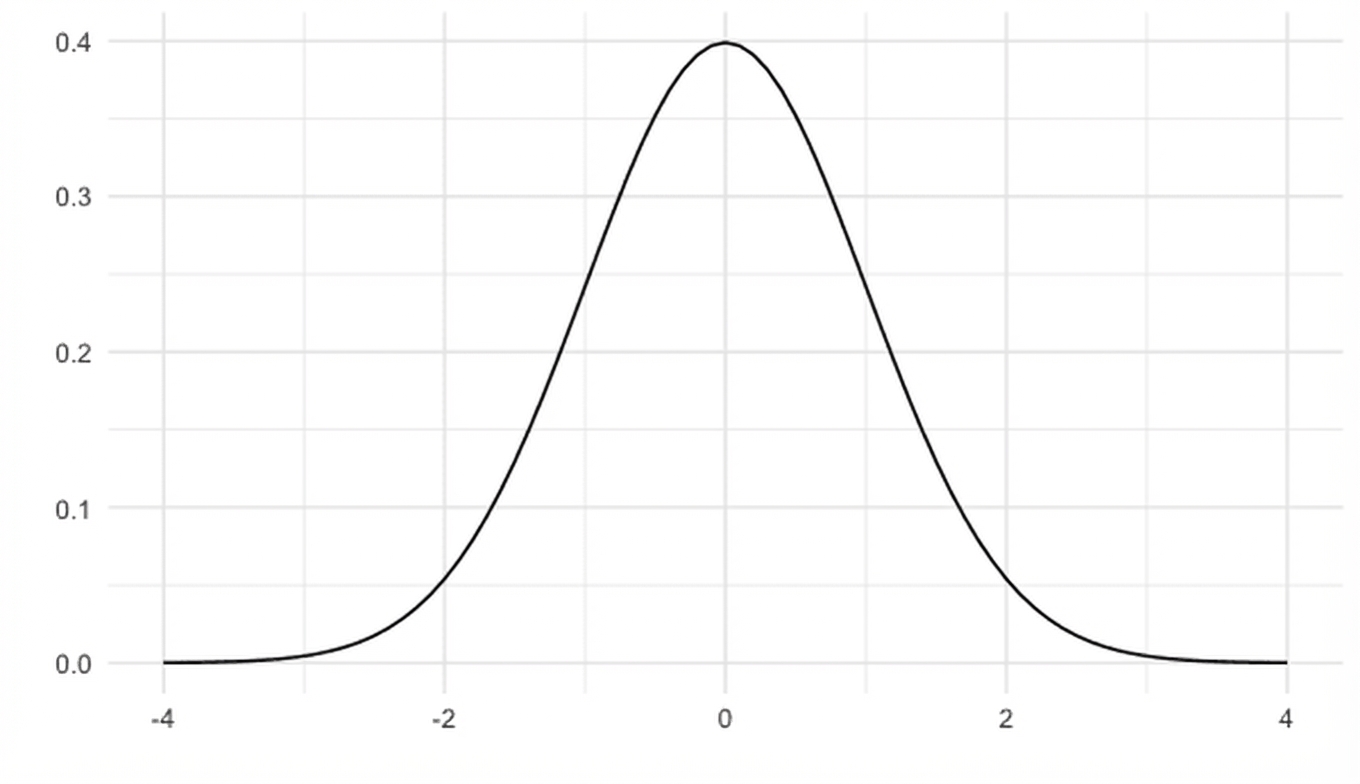
Dichtefunktion der Normalverteilung

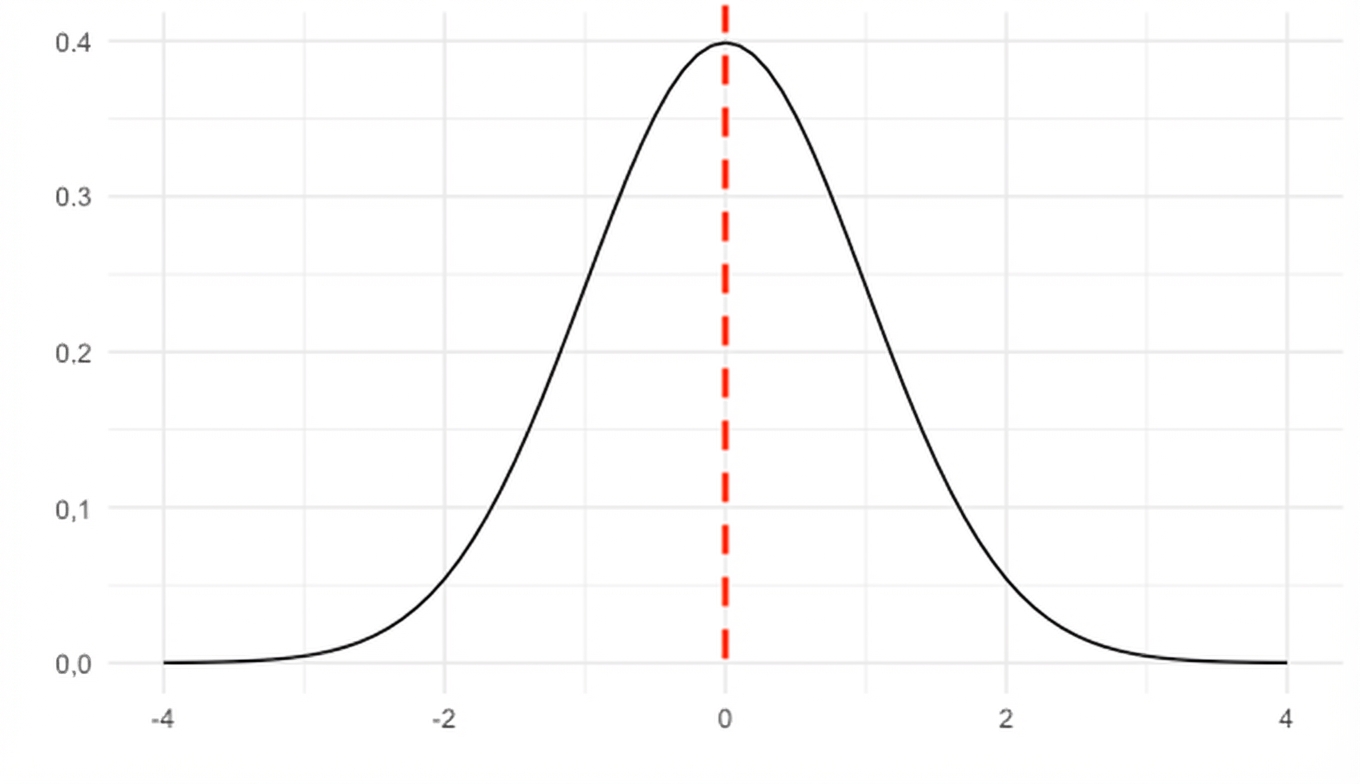
Symmetrisch

Gestrichelte vertikale Linie in der Mitte der Normalverteilung

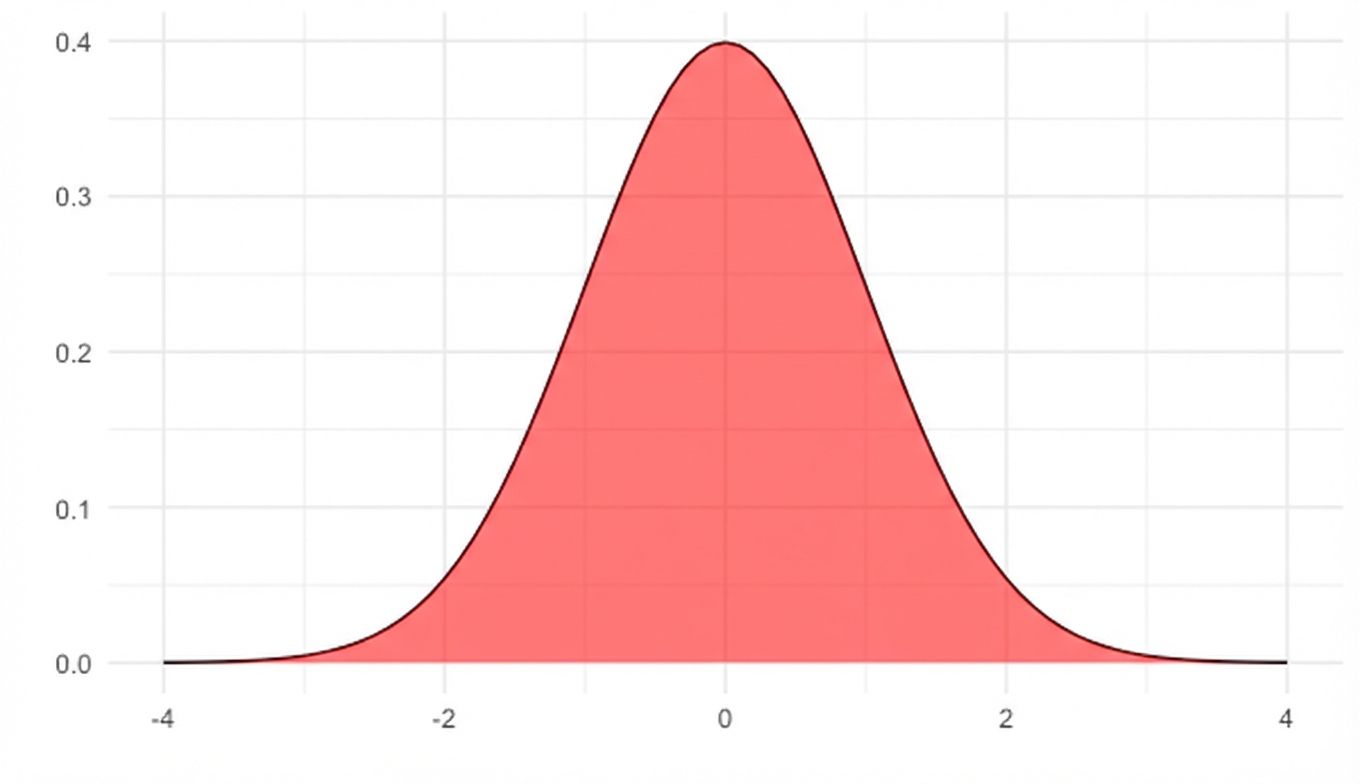
Fläche = 1

Normalverteilung mit schattierter Fläche unter der Kurve

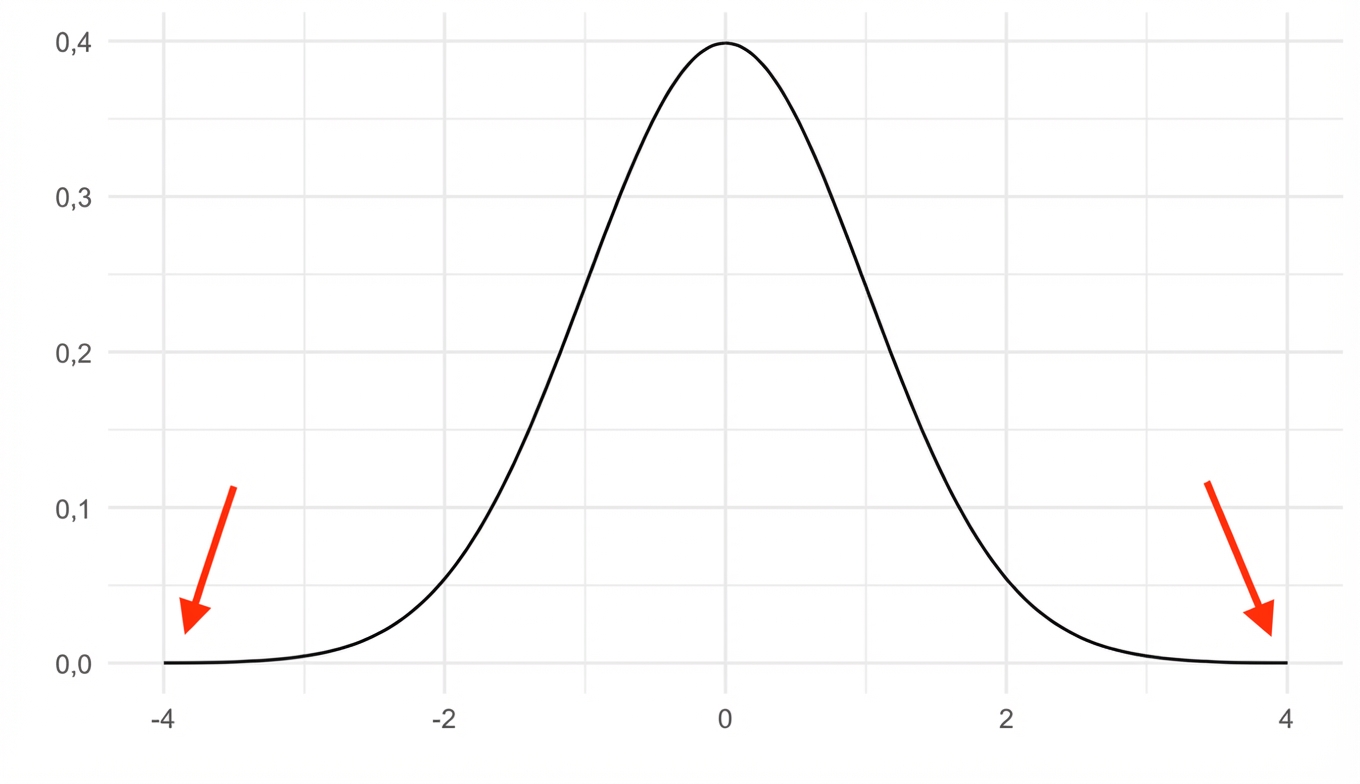
Kurve geht nie gegen 0

Normalverteilung mit Pfeilen, die auf die Ränder auf beiden Seiten zeigen

Beschrieben durch Mittelwert und Standardabweichung

Mittelwert: 20

Standardabweichung: 3

Normalverteilung mit Mittelwert 20 und Standardabweichung 3

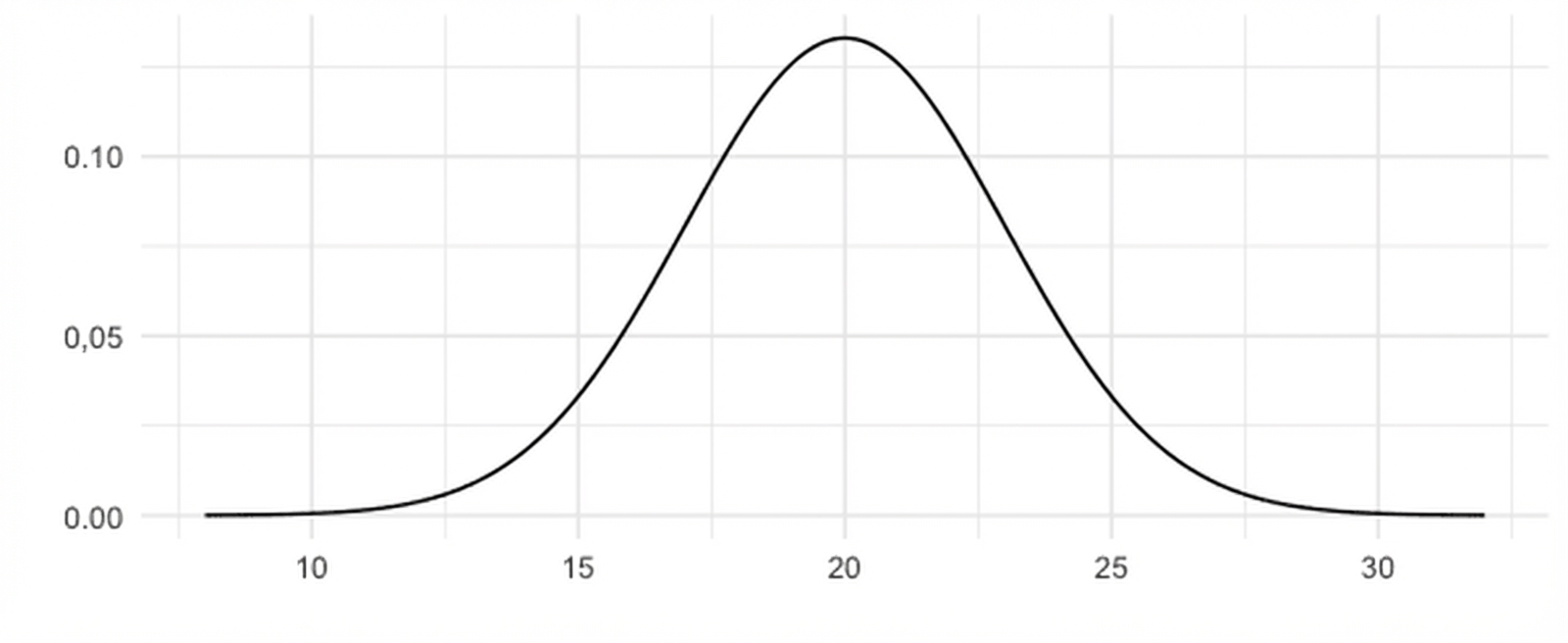
Standard-Normalverteilung

Mittelwert: 0

Standardabweichung: 1

Normalverteilung mit Mittelwert 0 und Standardabweichung 1

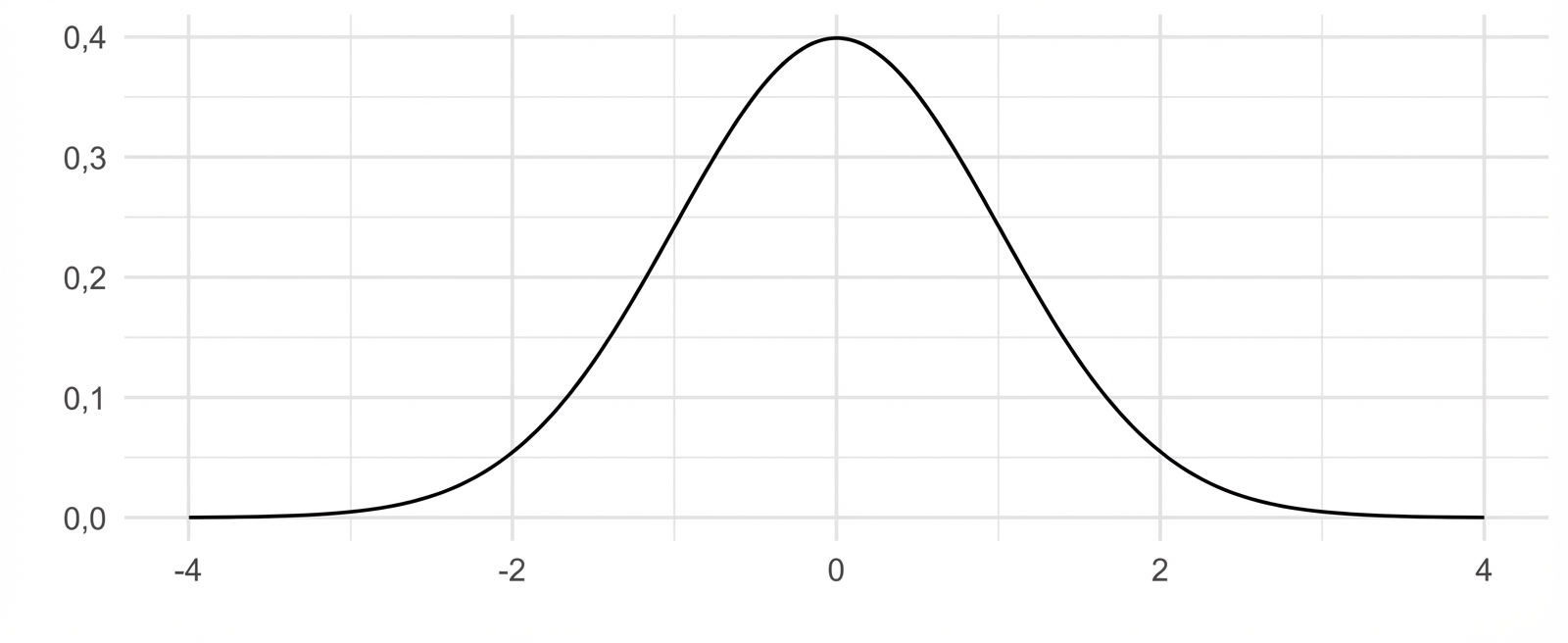
Beschrieben durch Mittelwert und Standardabweichung

Mittelwert: 20

Standardabweichung: 3

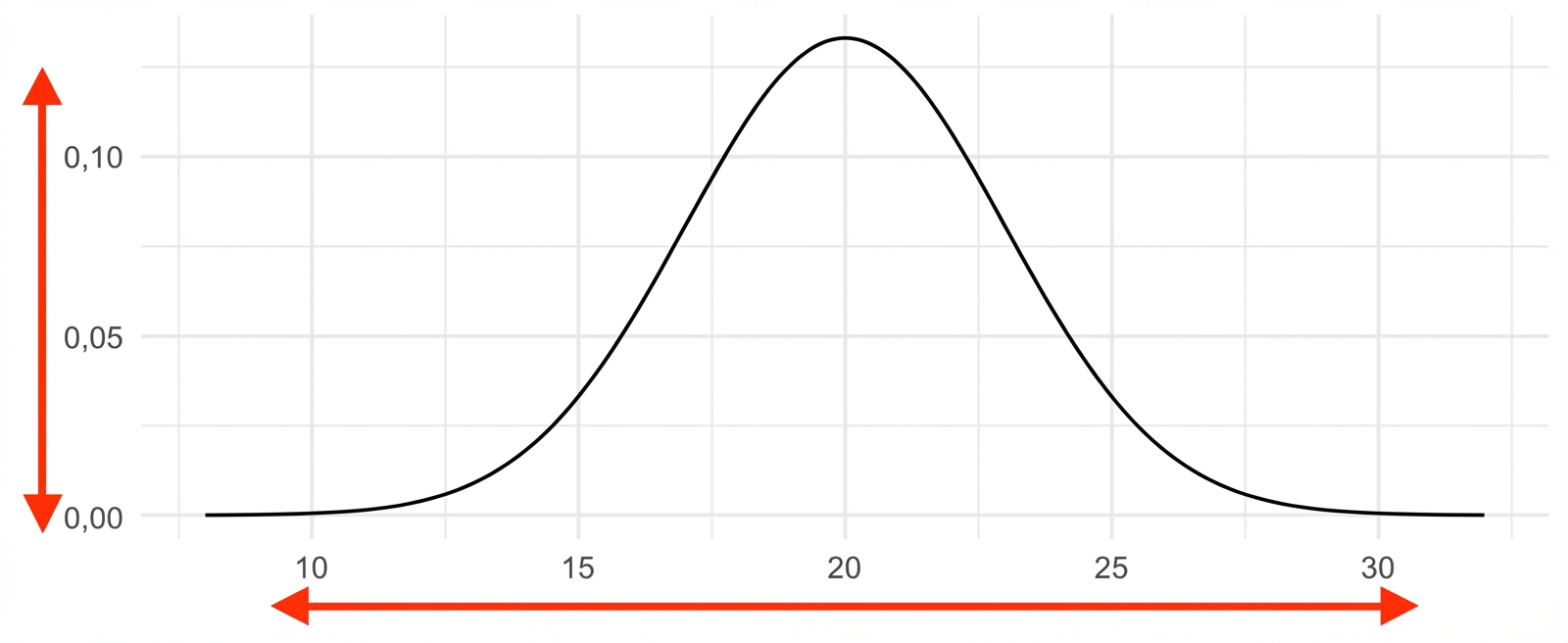
Normalverteilung mit Mittelwert 20 und Standardabweichung 3

Standard-Normalverteilung

Mittelwert: 0

Standardabweichung: 1

Normalverteilung mit Mittelwert 0 und Standardabweichung 1

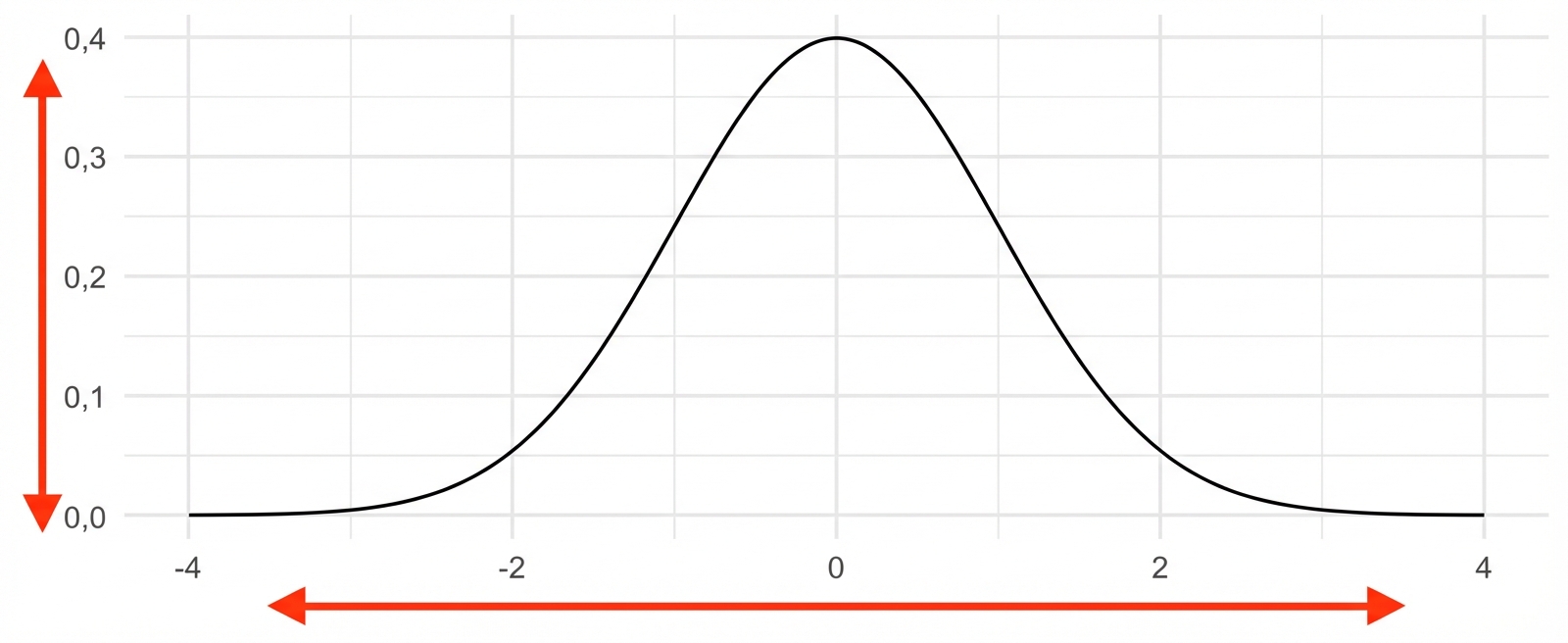
Flächen unterhalb der Normalverteilungskurve

68 % liegt innerhalb von 1 Standardabweichung

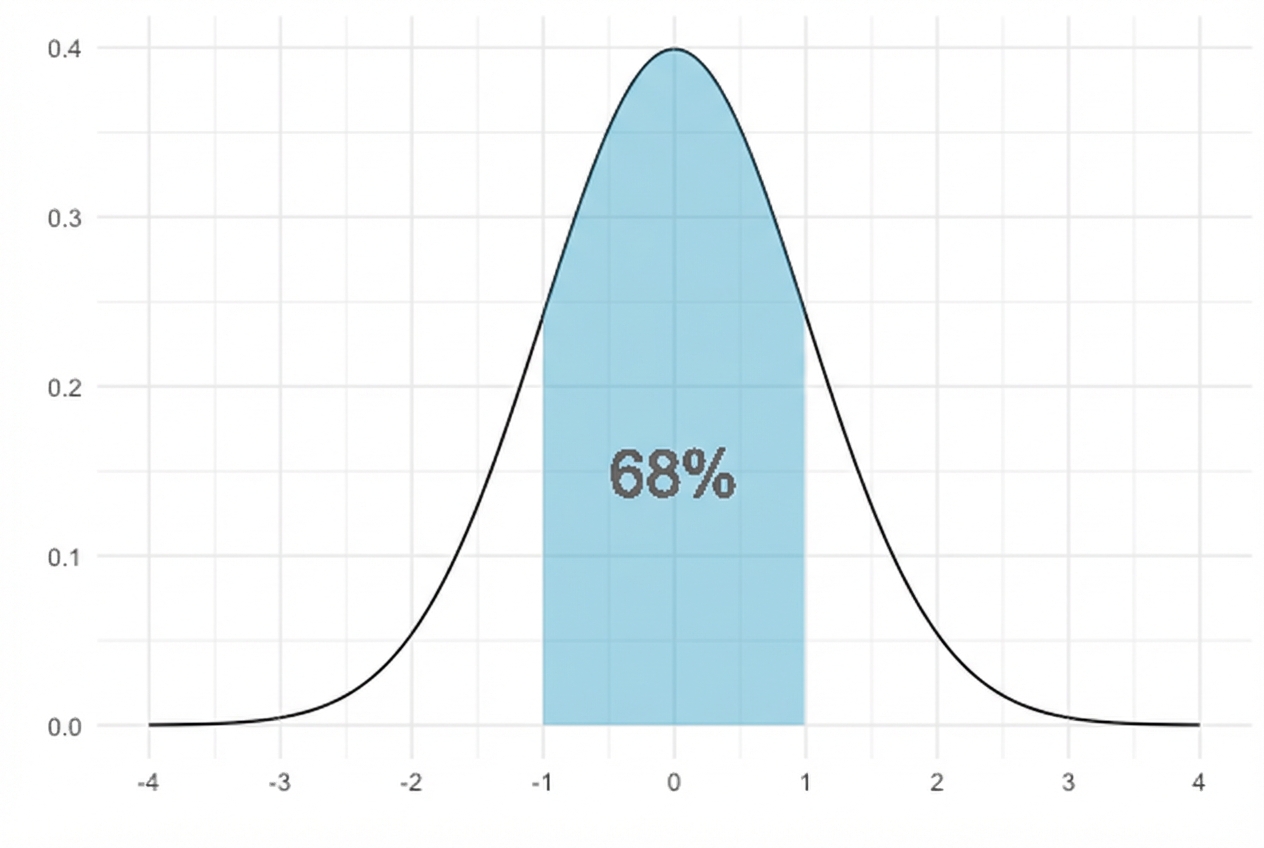
Normalverteilung mit hervorgehobenem Bereich zwischen -1 und 1, beschriftet mit 68 %

Flächen unterhalb der Normalverteilungskurve

95% liegt innerhalb von 2 Standardabweichungen

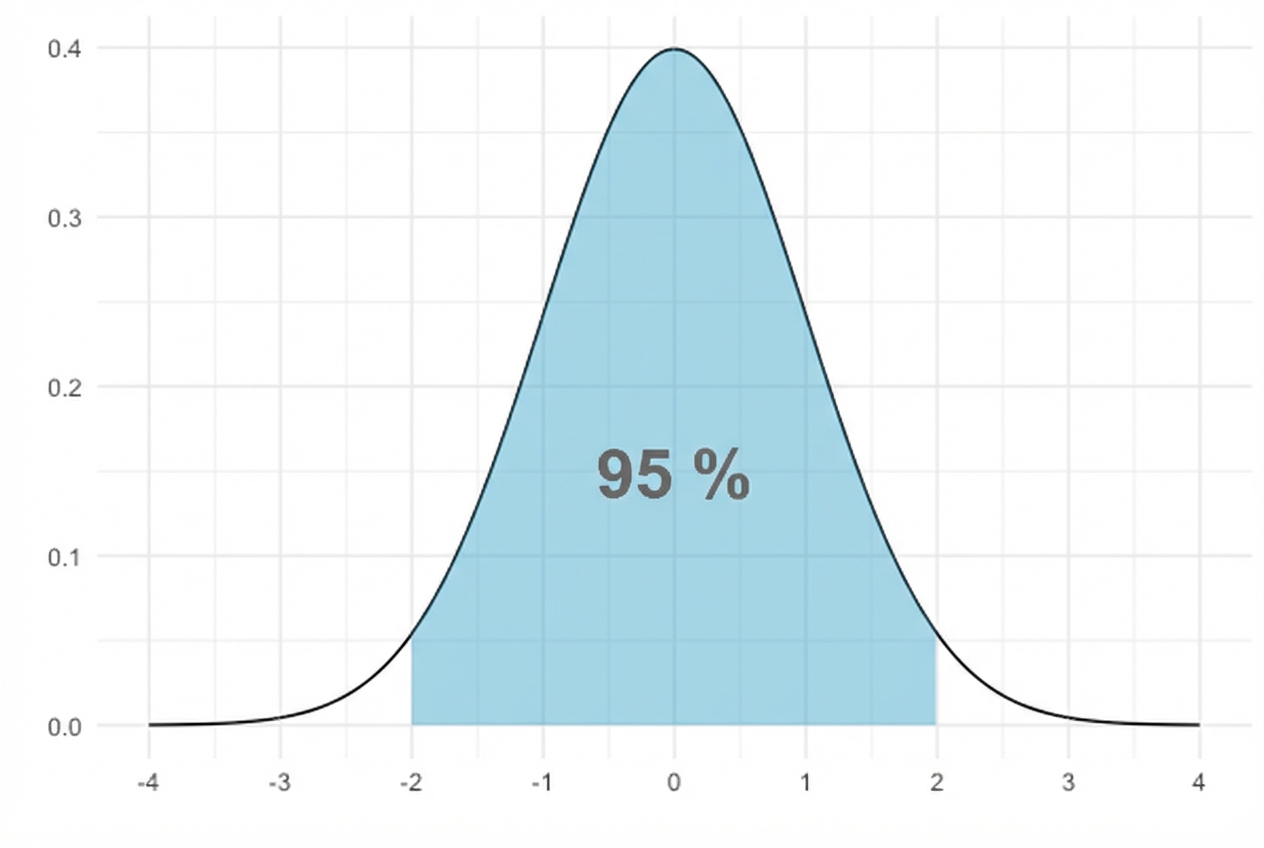
Normalverteilung mit hervorgehobenem Bereich zwischen -2 und 2, beschriftet mit 95%

Flächen unterhalb der Normalverteilungskurve

99,7% liegen innerhalb von 3 Standardabweichungen

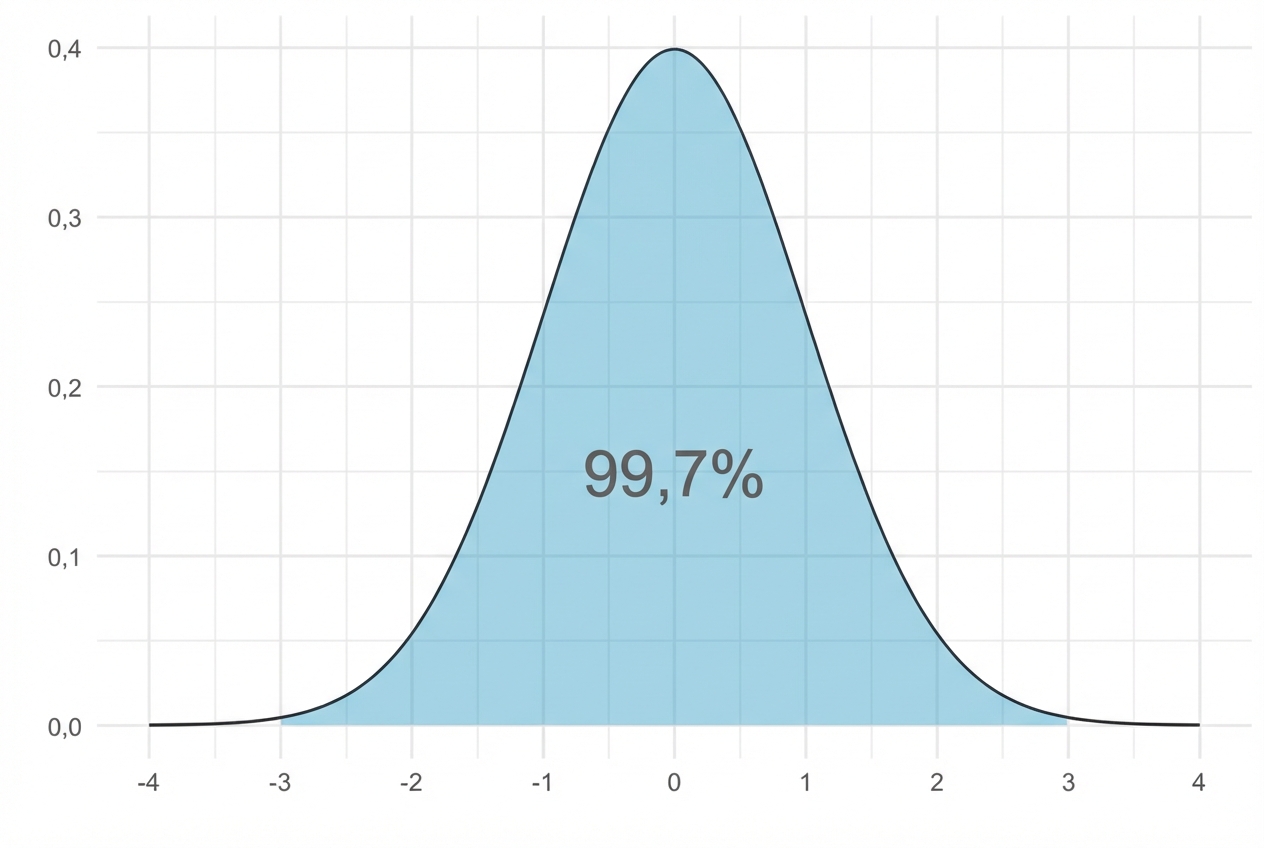
Normalverteilung mit hervorgehobenem Bereich zwischen -3 und 3, beschriftet mit 99,7%

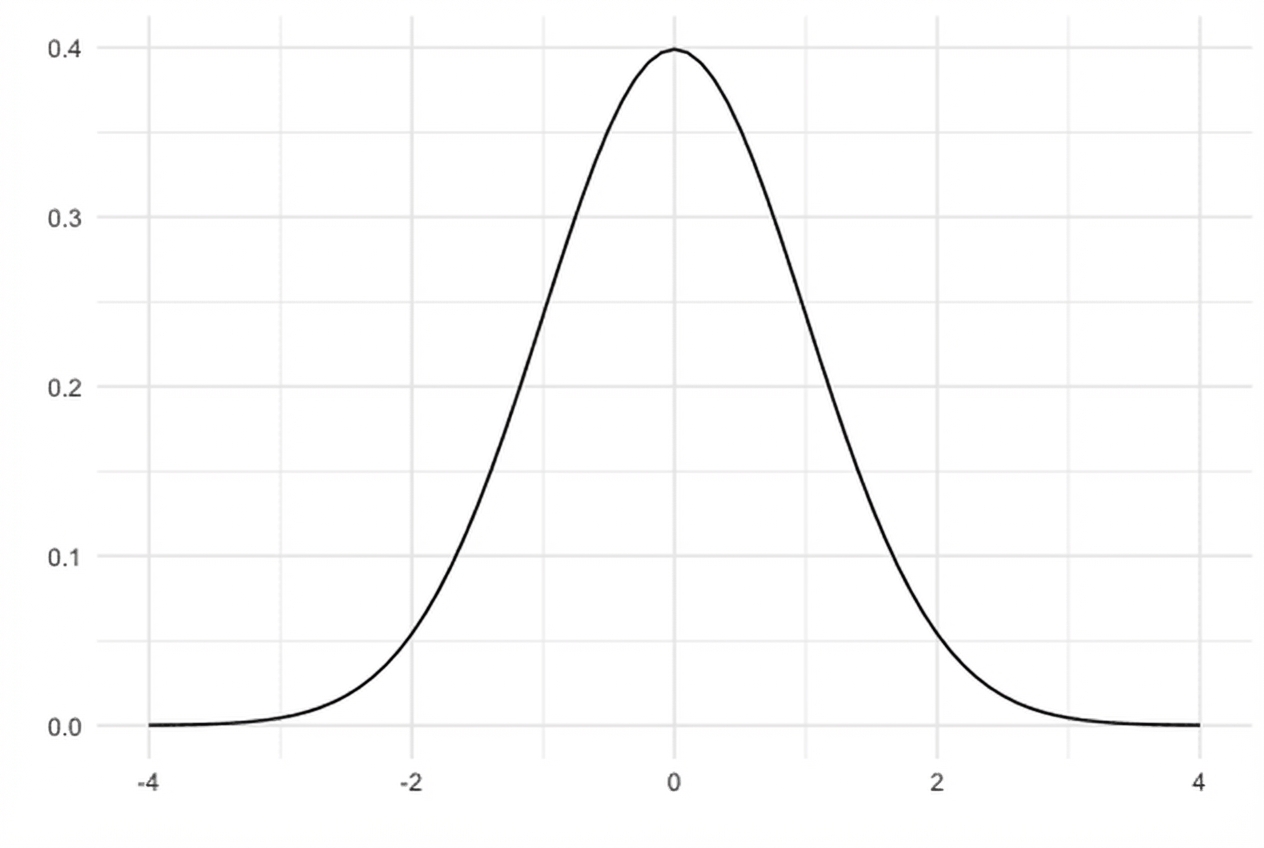
Viele Histogramme sehen wie Normalverteilungen aus

Normalverteilung

Standard-Normalverteilung

Körpergrößen von Frauen aus NHANES

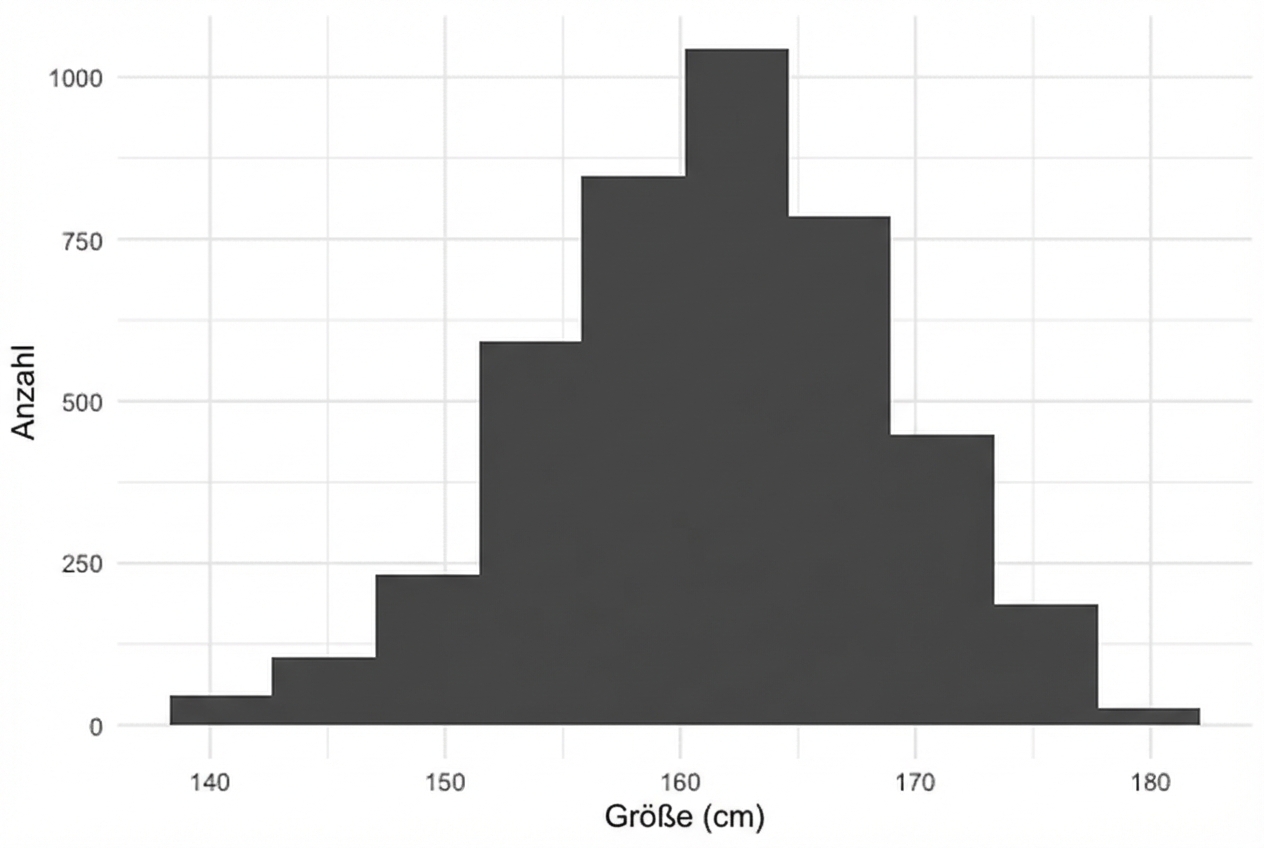
Histogramm der Körpergröße von Frauen

Mittelwert: 161 cm Standardabweichung: 7cm

Annäherung der Daten mit der Normalverteilung

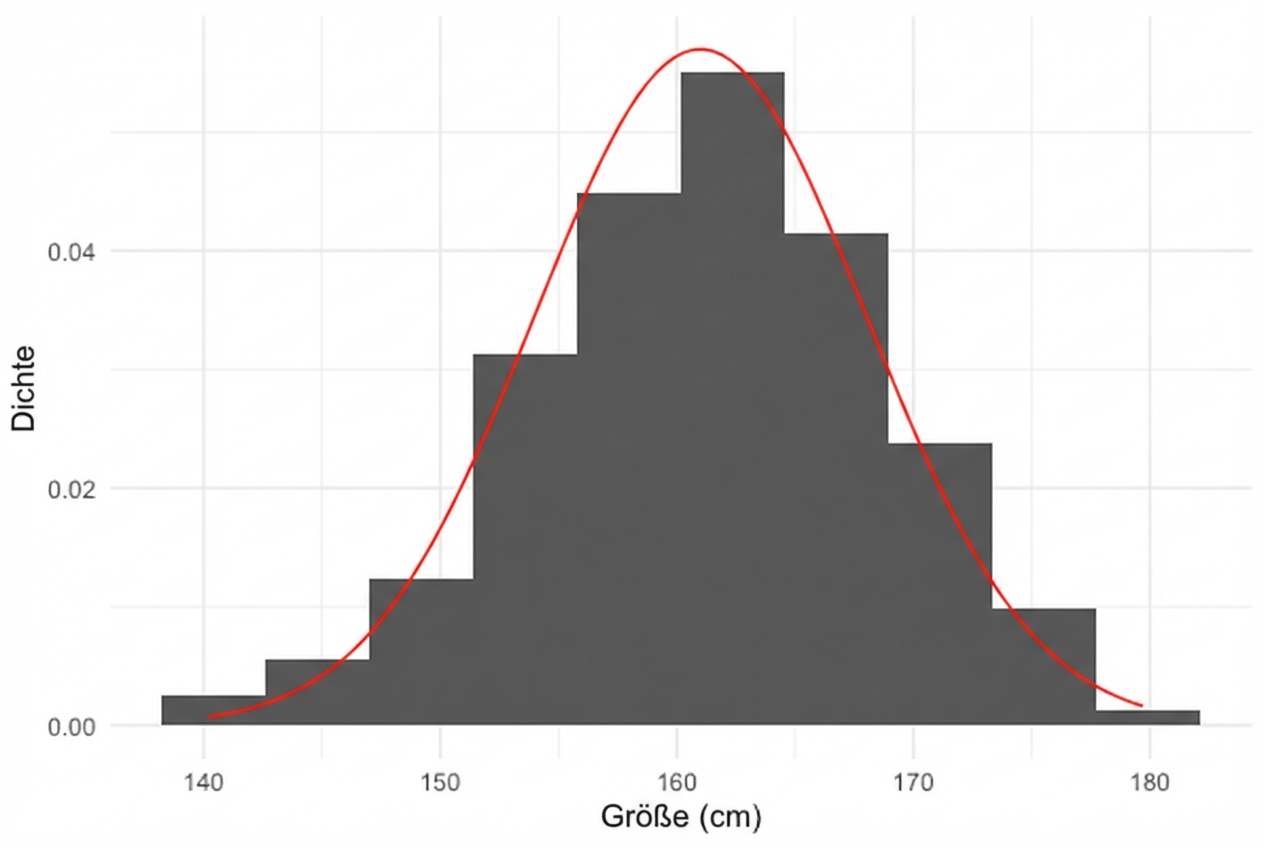
Normalkurve über dem Histogramm der Körpergröße von Frauen

Wie viel Prozent der Frauen sind kleiner als 154 cm?

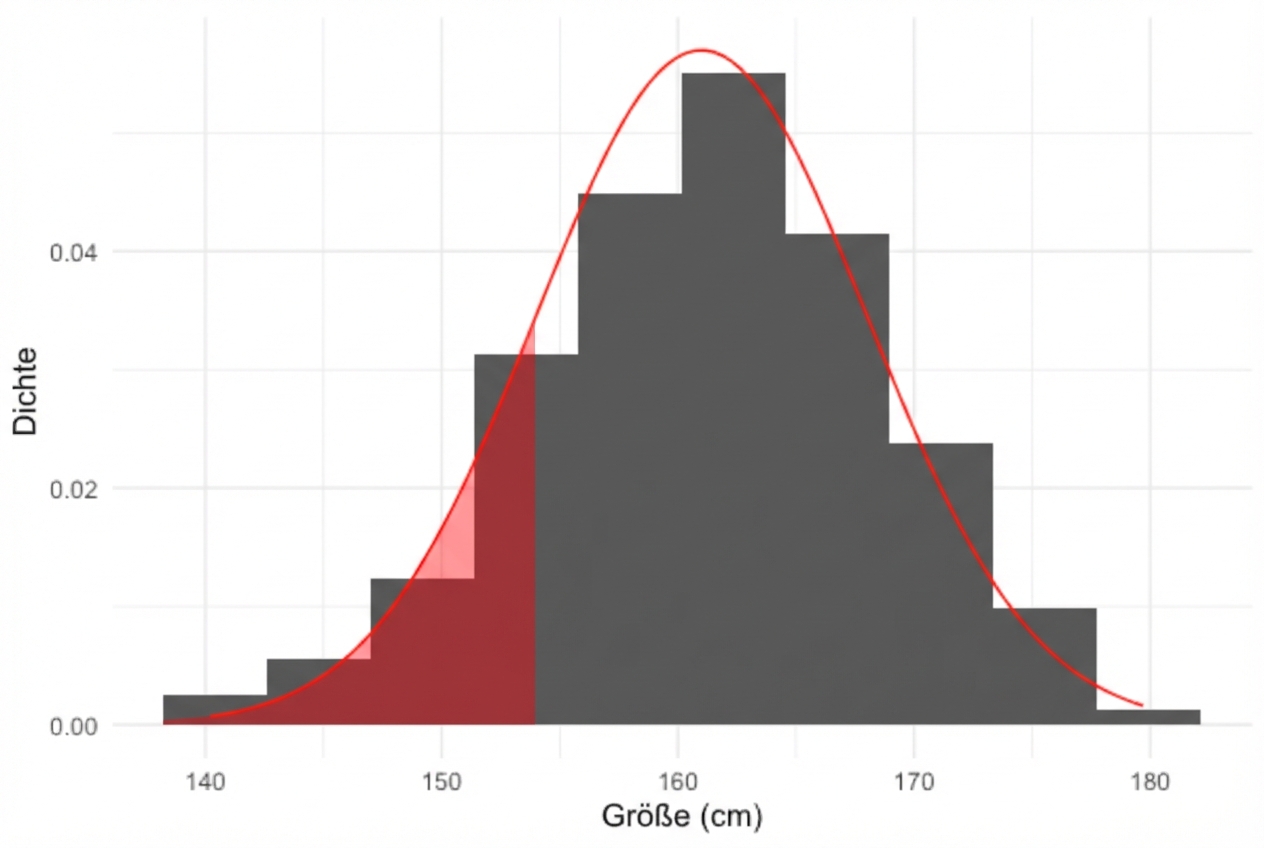
Normalkurve, die über das Histogramm der Körpergröße von Frauen gezeichnet wurde, wobei der Bereich unter 154 schattiert ist

16 % der Frauen in der Umfrage sind kleiner als 154 cm

pnorm(154, mean = 161, sd = 7)

0.159

Wie viel Prozent der Frauen sind größer als 154 cm?

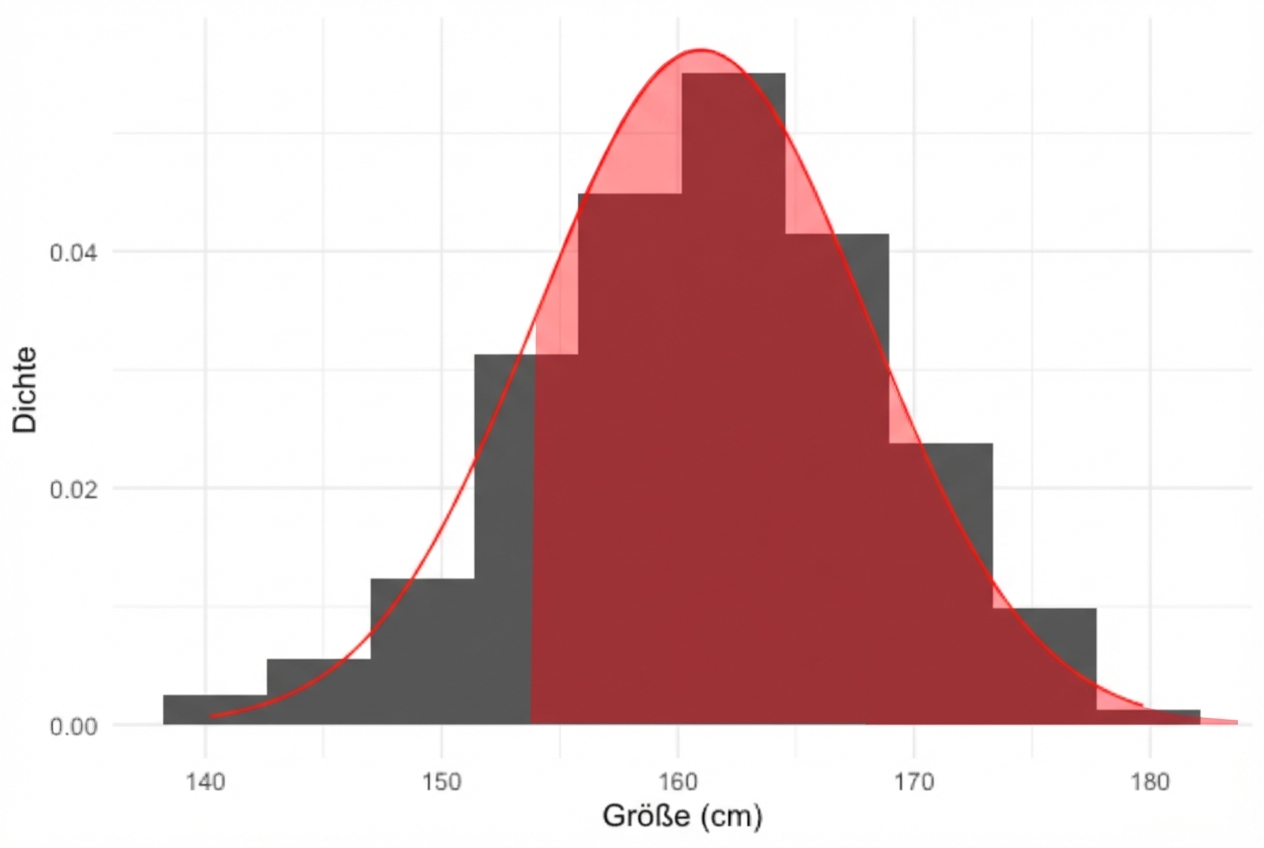
Normalkurve, die über das Histogramm der Körpergröße von Frauen gezeichnet wurde, wobei der Bereich rechts von 154 schattiert ist

pnorm(154, mean = 161, sd = 7, 
      lower.tail = FALSE)

0.8413447

Wie viel Prozent der Frauen sind 154-157 cm groß?

Fläche kleiner als 157 minus Fläche kleiner als 154

pnorm(157, mean = 161, sd = 7) - pnorm(154, mean = 161, sd = 7)

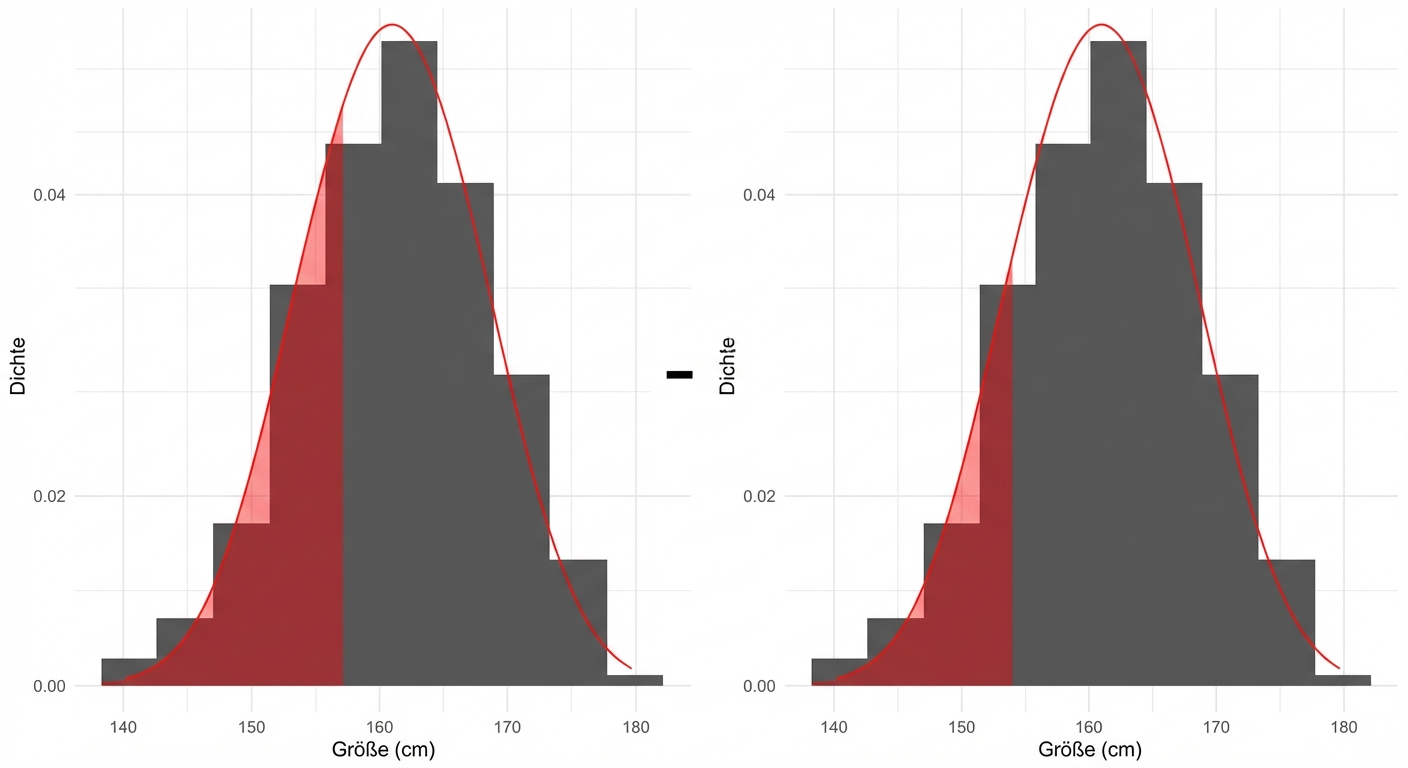
Wie viel Prozent der Frauen sind 154-157 cm groß?

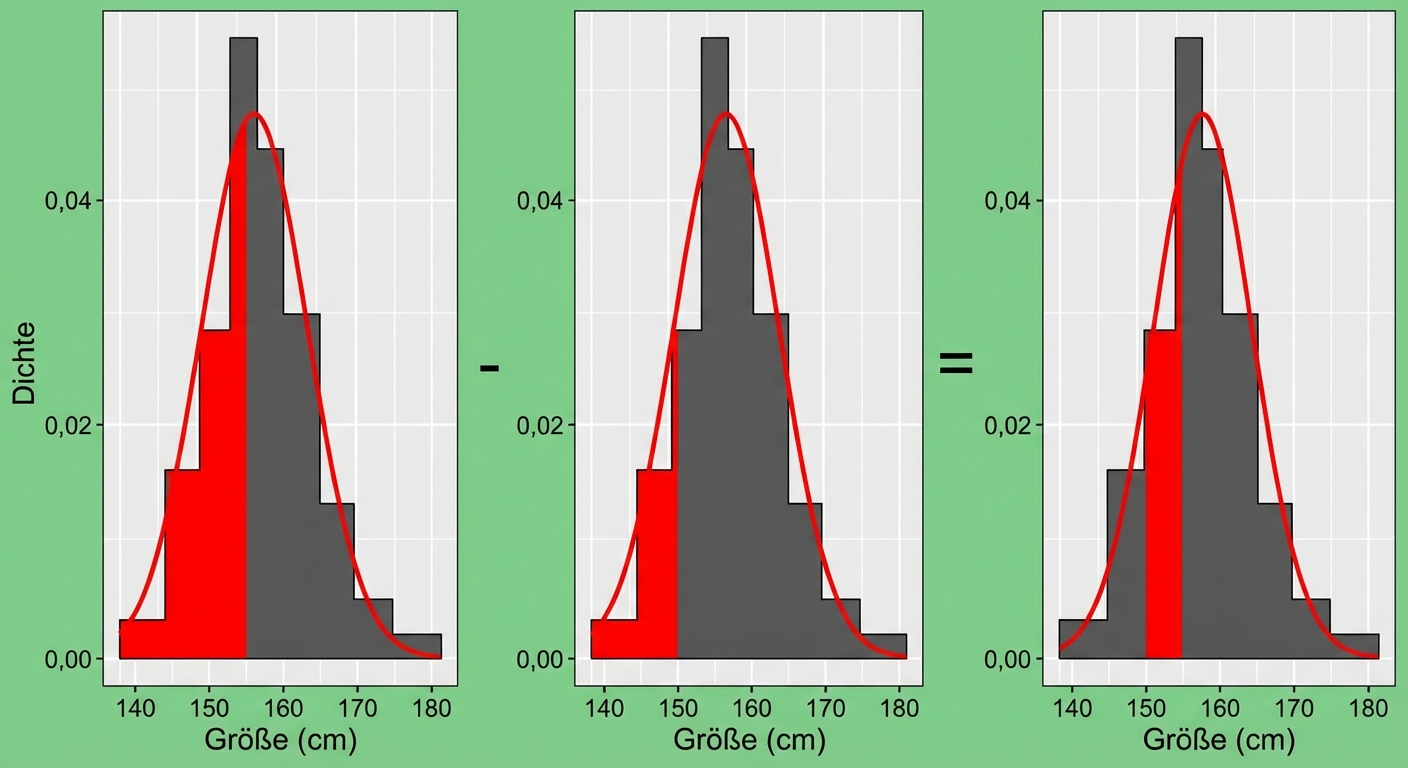
Fläche kleiner als 157 minus Fläche kleiner als 154 ist gleich Fläche zwischen 154 und 157

pnorm(157, mean = 161, sd = 7) - pnorm(154, mean = 161, sd = 7)

0.1252

Welche Größe unterschreiten 90 % der Frauen?

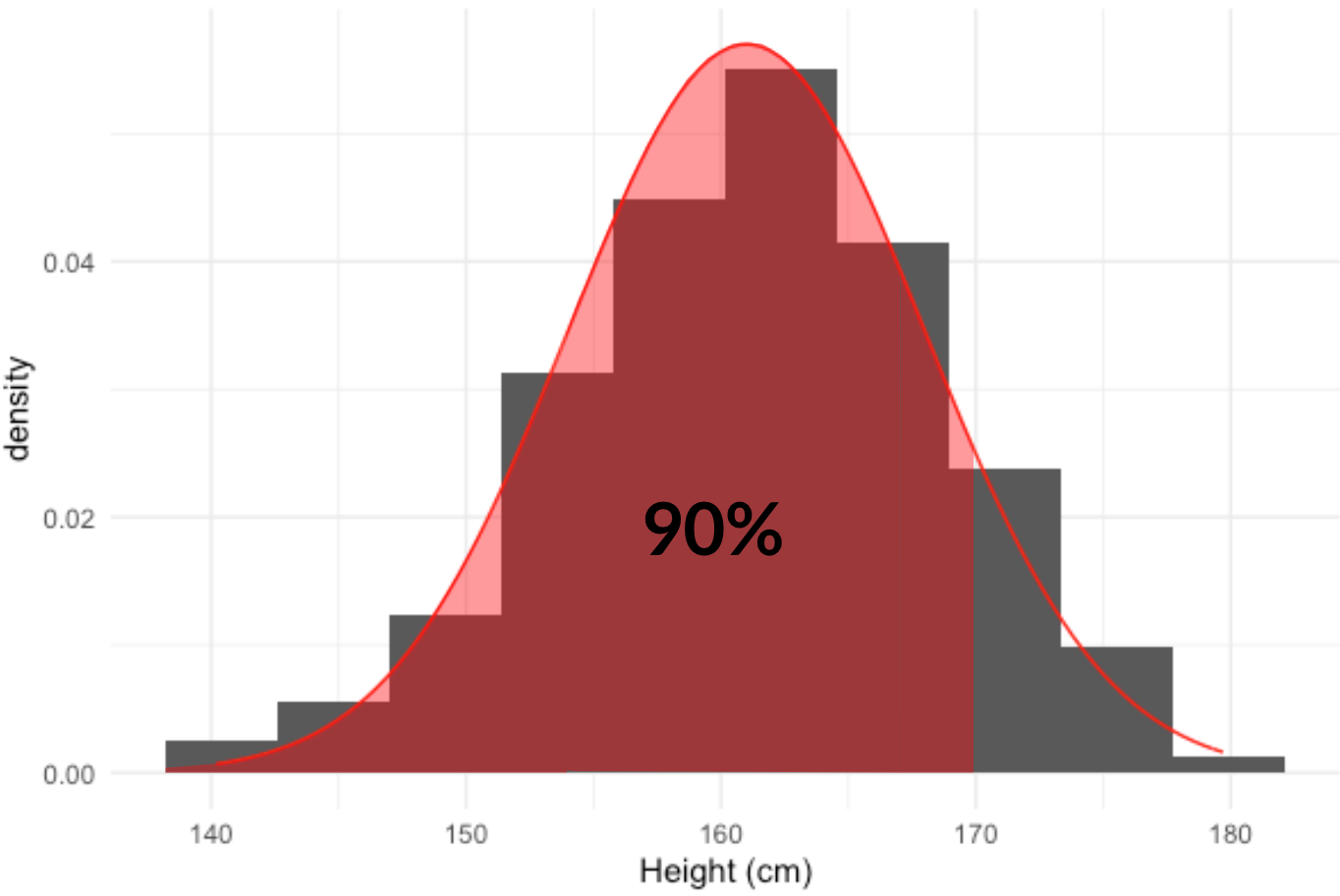
Fläche weniger als 170 schattiert, beschriftet 90 %

qnorm(0.9, mean = 161, sd = 7)

169.9709

Welche Größe übertreffen 90 % der Frauen?

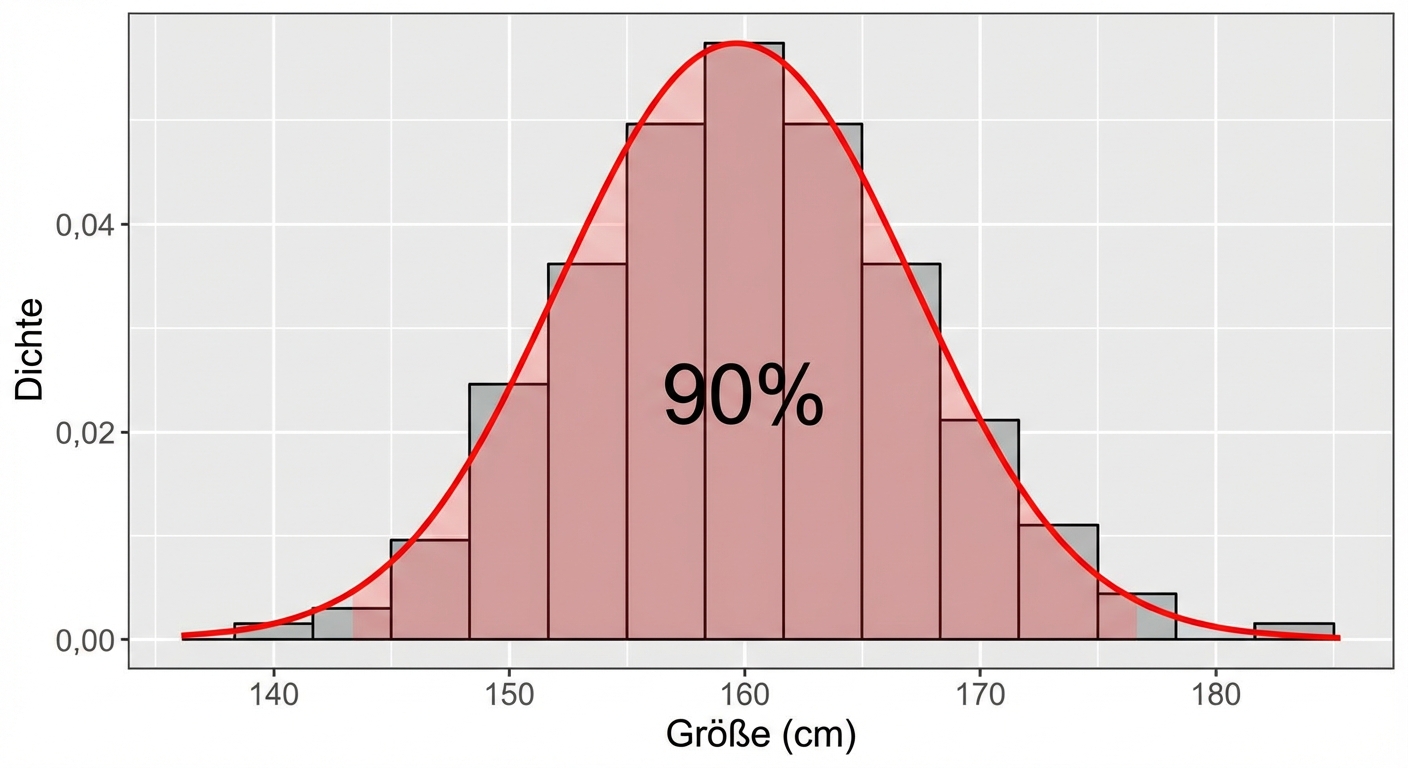
Fläche größer als etwa 162 schattiert, beschriftet 90 %

qnorm(0.9,
      mean = 161,
      sd = 7,
      lower.tail = FALSE)

152.03

Zufällige Zahlen generieren

# Generate 10 random heights
rnorm(10, mean = 161, sd = 7)

159.35 157.34 149.85 156.75 163.53 156.33 157.22 171.44 158.10 170.12

Lass uns üben!

Einführung in die Statistik in R

Preparing Video For Download...