Der zentrale Grenzwertsatz

Einführung in die Statistik in R

Maggie Matsui

Content Developer, DataCamp

5 mal würfeln

die <- c(1, 2, 3, 4, 5, 6)

# Roll 5 times
sample_of_5 <- sample(die, 5,
                      replace = TRUE)
sample_of_5

1 3 4 1 1

mean(sample_of_5)

2.0

sechsseitiger Würfel

5 mal würfeln

# Roll 5 times and take mean
sample(die, 5, replace = TRUE) %>% mean()

4.4

sample(die, 5, replace = TRUE) %>% mean()

3.8

5 mal würfeln 10 mal würfeln

10 mal wiederholen:

5 mal würfeln
Mittelwert nehmen

sample_means <- replicate(10, sample(die, 5, replace = TRUE) %>% mean())

sample_means

3.8 4.0 3.8 3.6 3.2 4.8 2.6 3.0 2.6 2.0

Stichprobenverteilungen

Stichprobenverteilung des Stichprobenmittelwerts

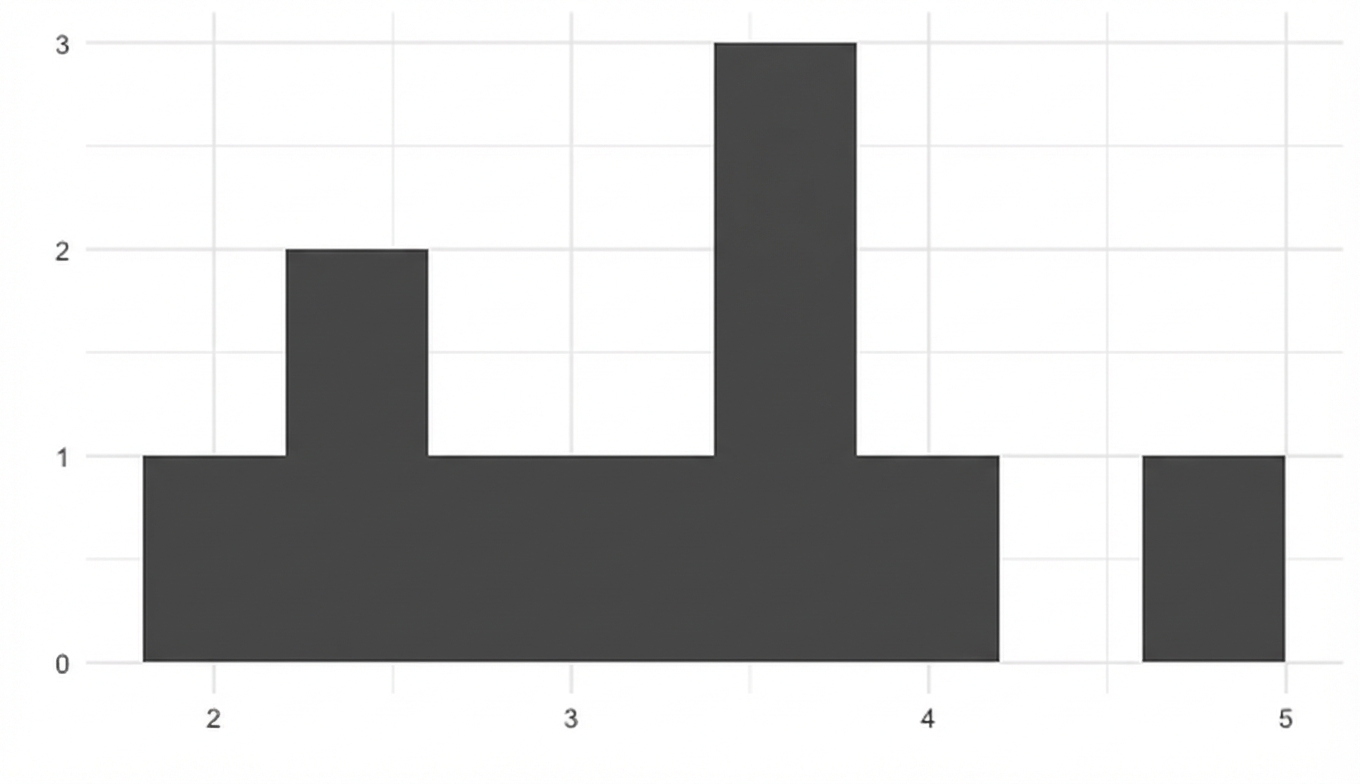
Histogramm von 10 Stichprobenmittelwerten

Mittelwerte von 100 Stichproben

replicate(100, sample(die, 5, replace = TRUE) %>% mean())

2.8 3.2 1.8 4.6 4.0 2.8 4.4 2.4 3.4 2.8 4.2 3.4 ... 2.2 3.8 3.6 3.8 4.4 4.8 2.4

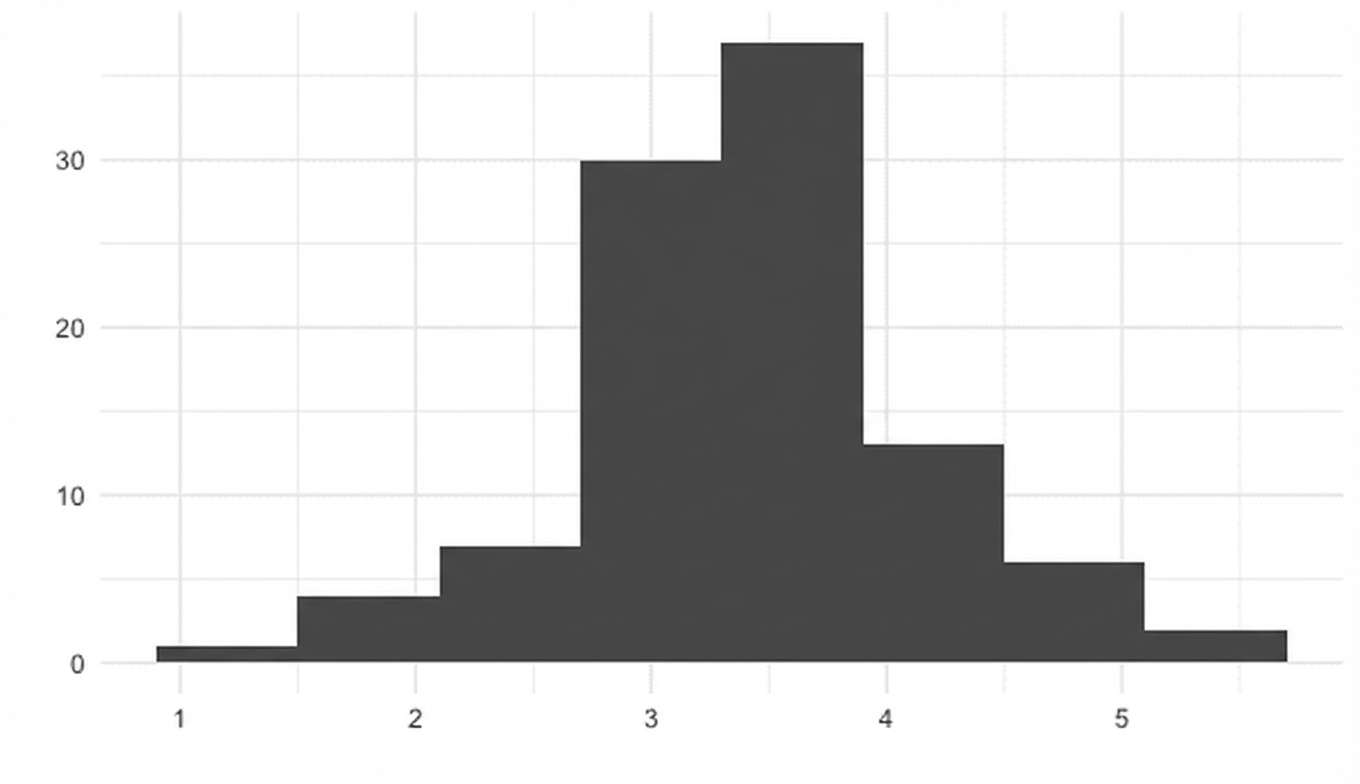
Histogramm von 100 Stichprobenmittelwerten

Mittelwerte von 1000 Stichproben

sample_means <- replicate(1000, sample(die, 5, replace = TRUE) %>% mean())

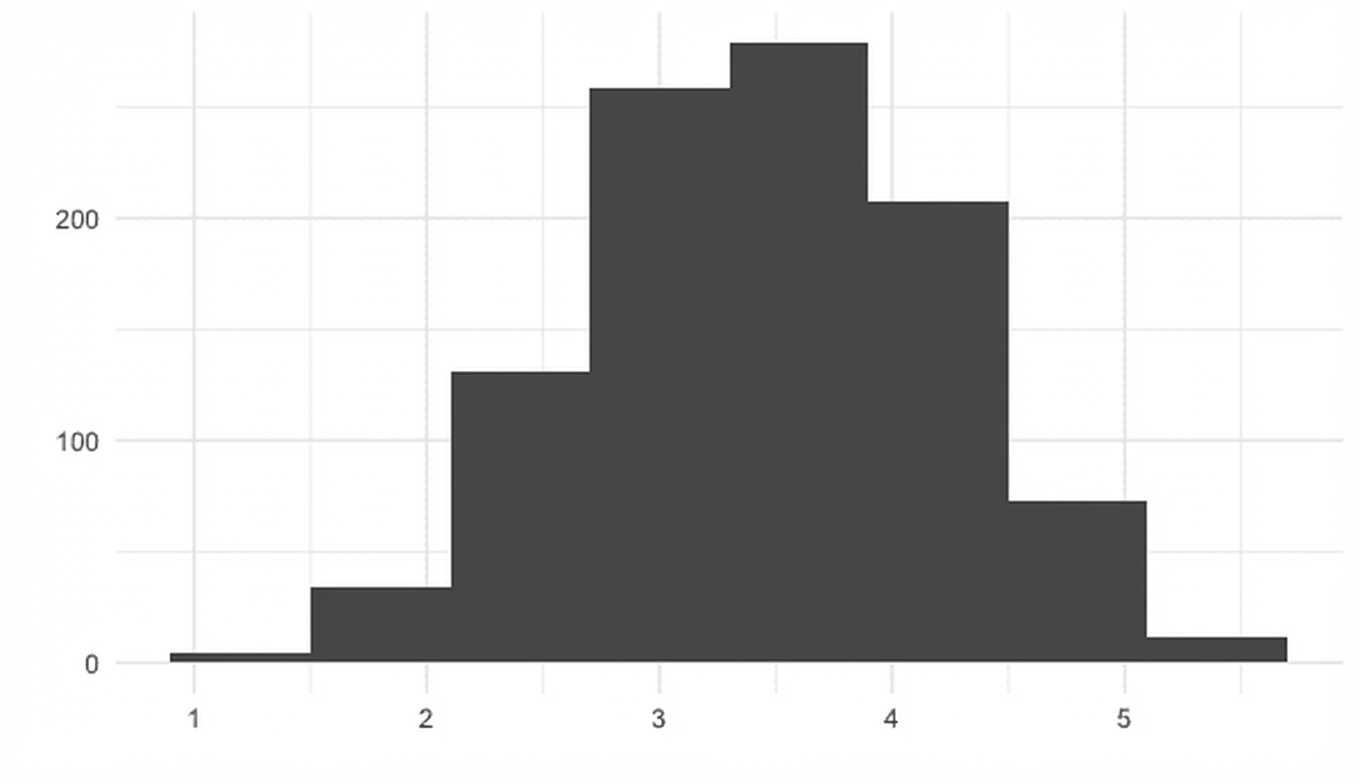
Histogramm von 1000 Stichprobenmittelwerten

Zentraler Grenzwertsatz

Die Stichprobenverteilung einer Statistik nähert sich mit zunehmender Anzahl von Versuchen immer mehr der Normalverteilung an.

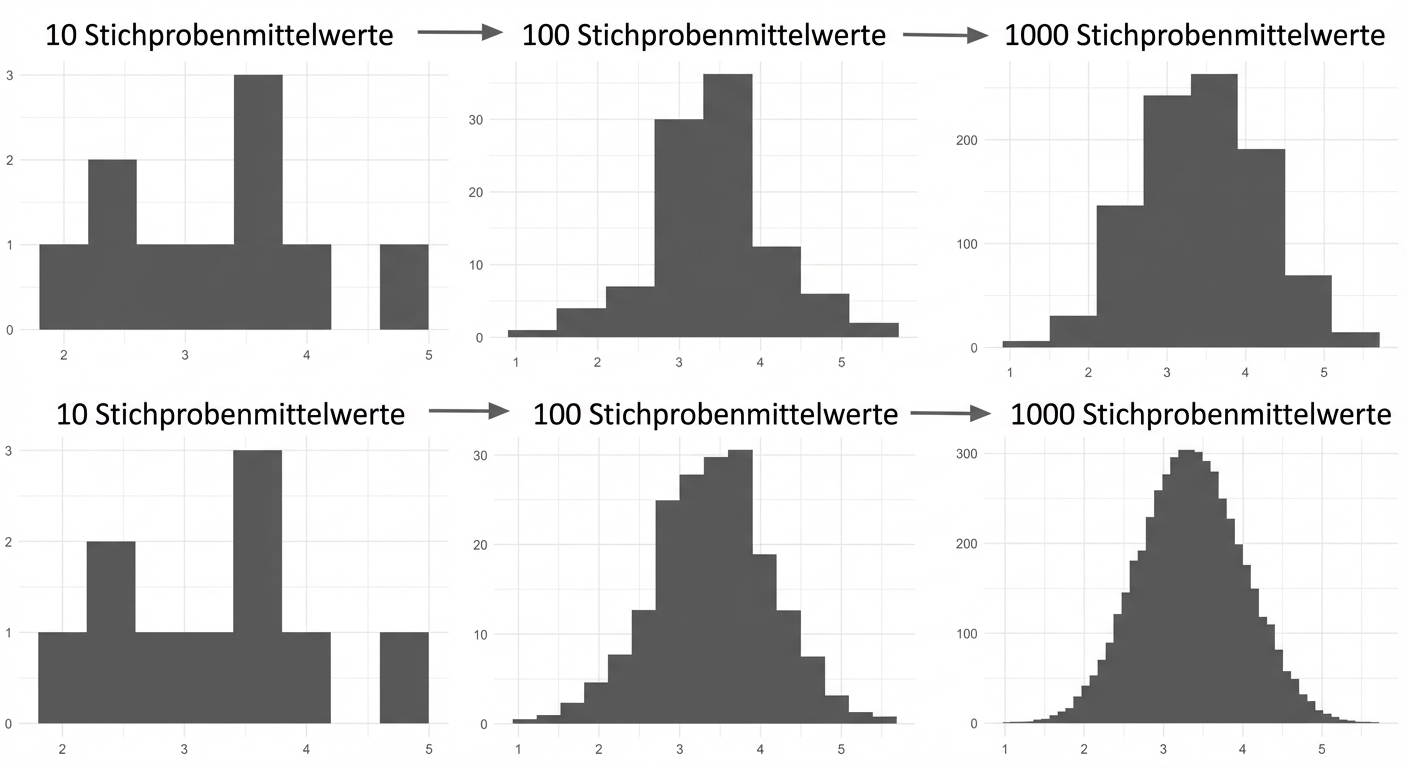
Histogramme von 10, 100 und 1000 Stichprobenmittelwerten, wobei eine höhere Anzahl von Stichprobenmittelwerten eine eher glockenförmige Verteilung aufweist

Stichproben sollten zufällig und unabhängig sein

Standardabweichung und der Grenzwertsatz

replicate(1000, sample(die, 5, replace = TRUE) %>% sd())

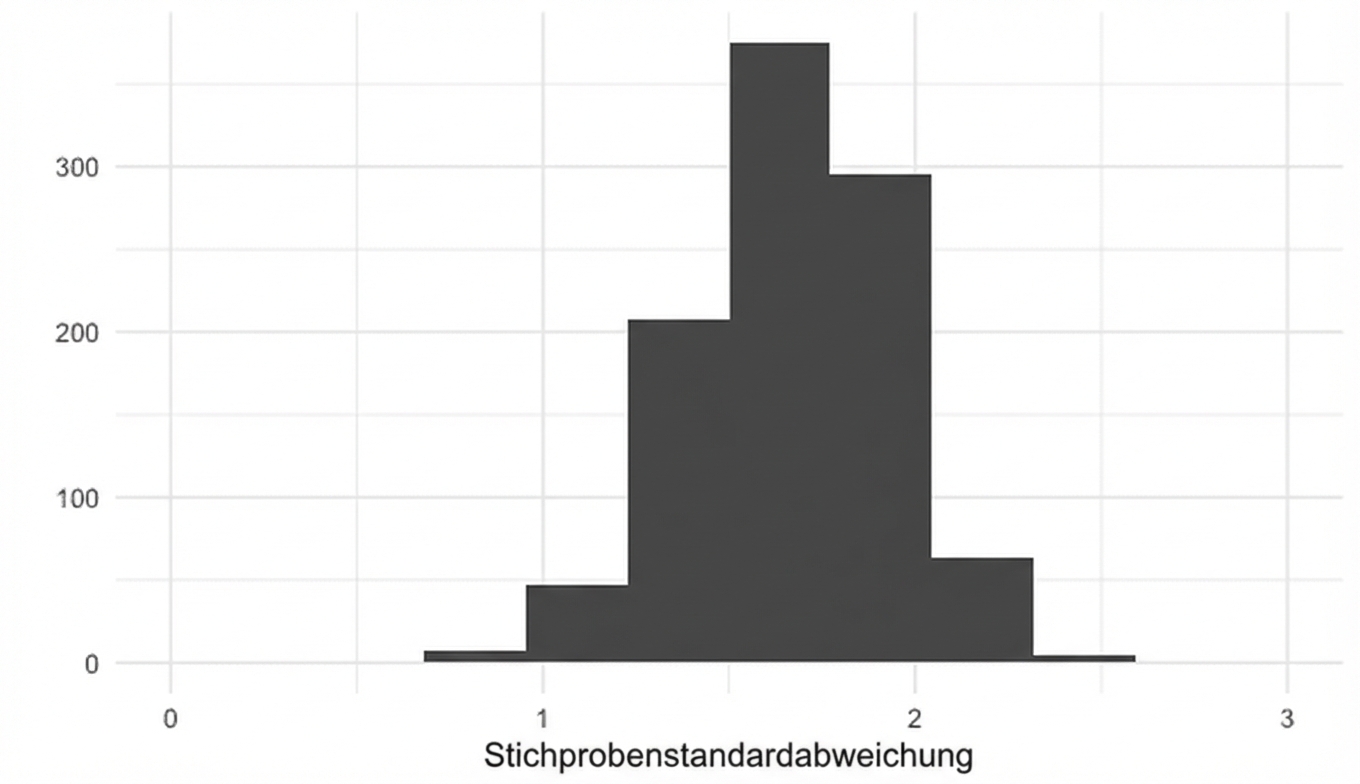
Verteilung von 1000 Stichproben-Standardabweichungen von 5 Würfelwürfen

Mengenanteile und der Grenzwertsatz

sales_team <- c("Amir", "Brian", "Claire", "Damian")

sample(sales_team, 10, replace = TRUE)

"Claire" "Brian"  "Brian"  "Brian"  "Damian" "Damian" "Brian"  "Brian" 
"Amir"   "Amir"

sample(sales_team, 10, replace = TRUE)

"Amir"   "Amir"   "Claire" "Amir"   "Amir"   "Brian"  "Amir"   "Claire" 
"Claire" "Claire"

Stichprobenverteilung der Mengenanteile

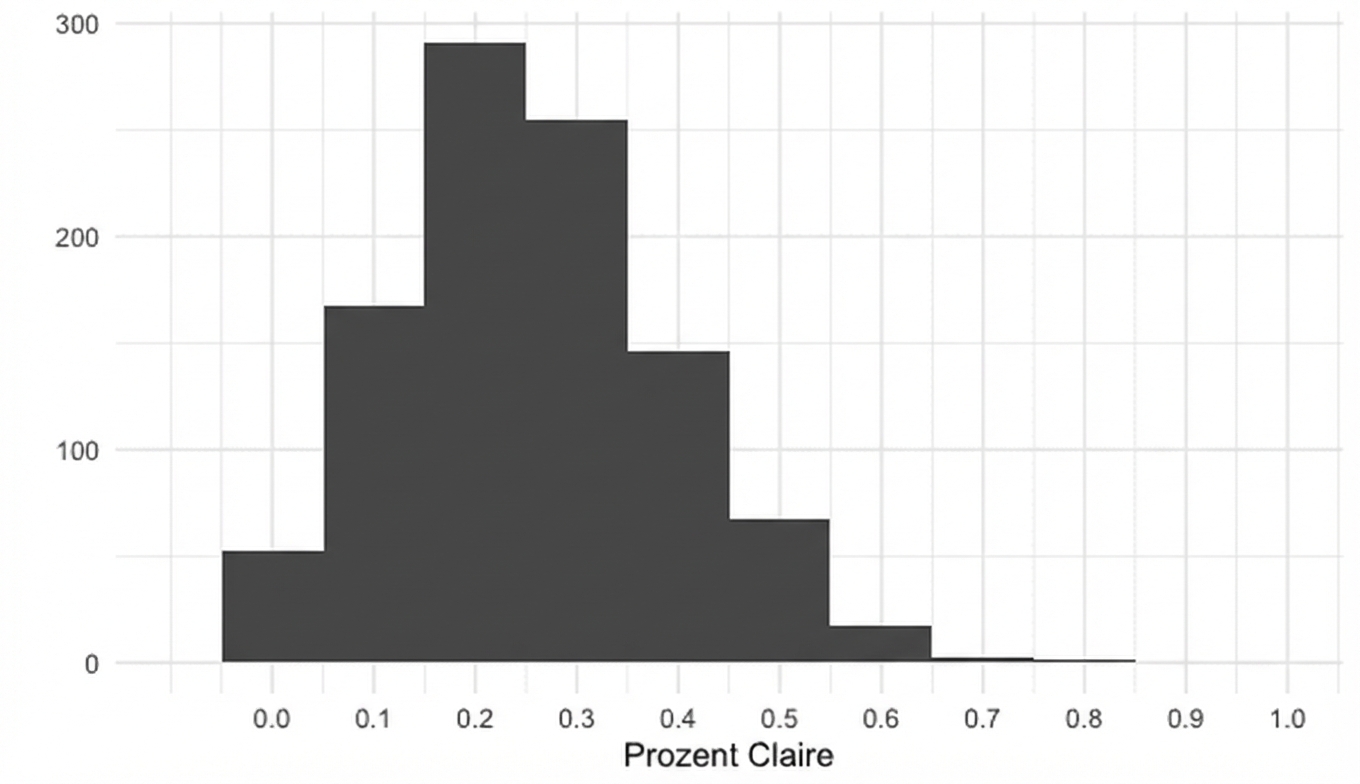
Die Verteilung der Stichprobenanteile sieht auch normal aus

Mittelwert der Stichprobenverteilung

# Estimate expected value of die
mean(sample_means)

3.48

# Estimate proportion of "Claire"s
mean(sample_props)

0.26

Merkmale der unbekannten zugrunde liegenden Verteilung schätzen

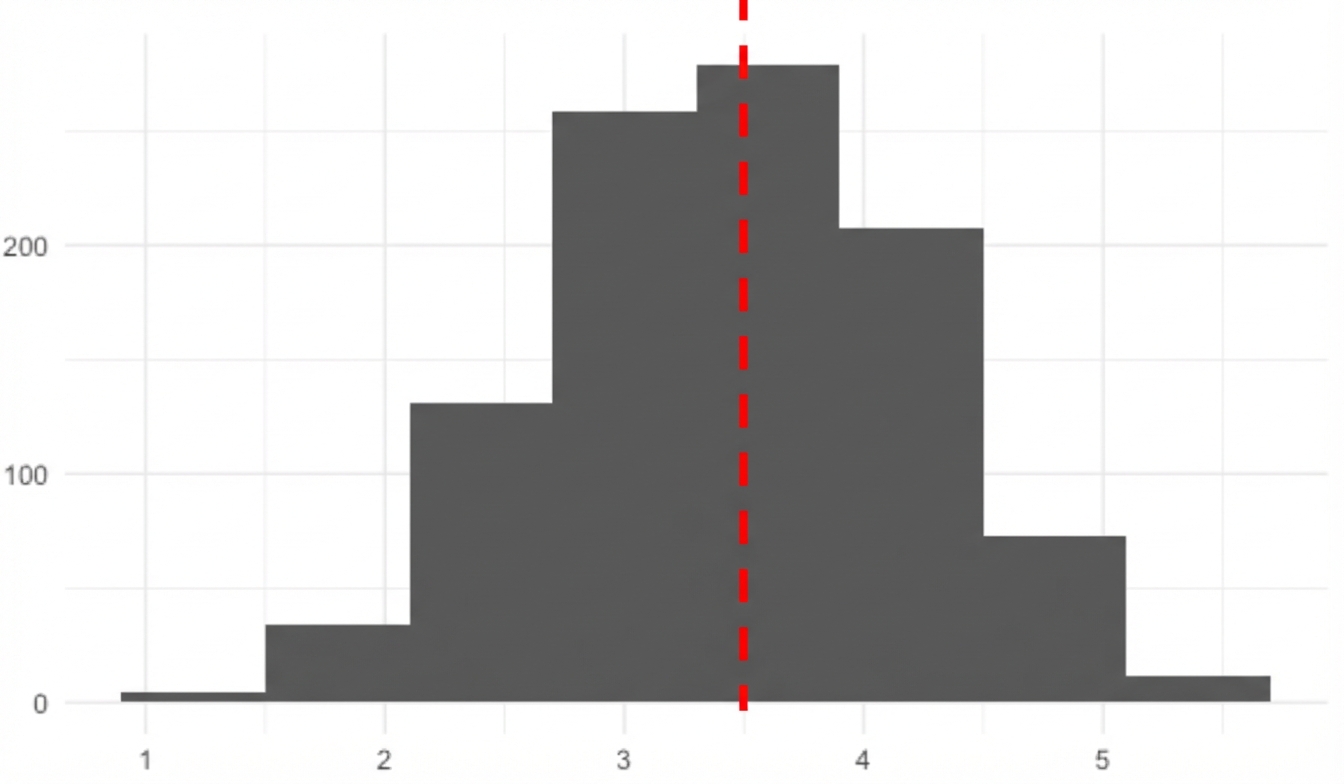
Stichprobenverteilung der Stichprobenmittelwerte mit gestrichelter Linie in der Mitte

Einfachere Schätzung von Merkmalen großer Datenmengen

Lass uns üben!

Einführung in die Statistik in R