Wie stehen die Chancen?
Einführung in die Statistik in R

Maggie Matsui
Content Developer, DataCamp
Messen von Wahrscheinlichkeiten
Wie hoch ist die Wahrscheinlichkeit eines Ereignisses?
$$ P(\text{event}) = \frac{\text{\# ways event can happen}}{\text{total \# of possible outcomes}} $$
Beispiel: Münzwurf
$$ P(\text{heads}) = \frac{\text{1 way to get heads}}{\text{2 possible outcomes}} = \frac{1}{2} = 50\%$$
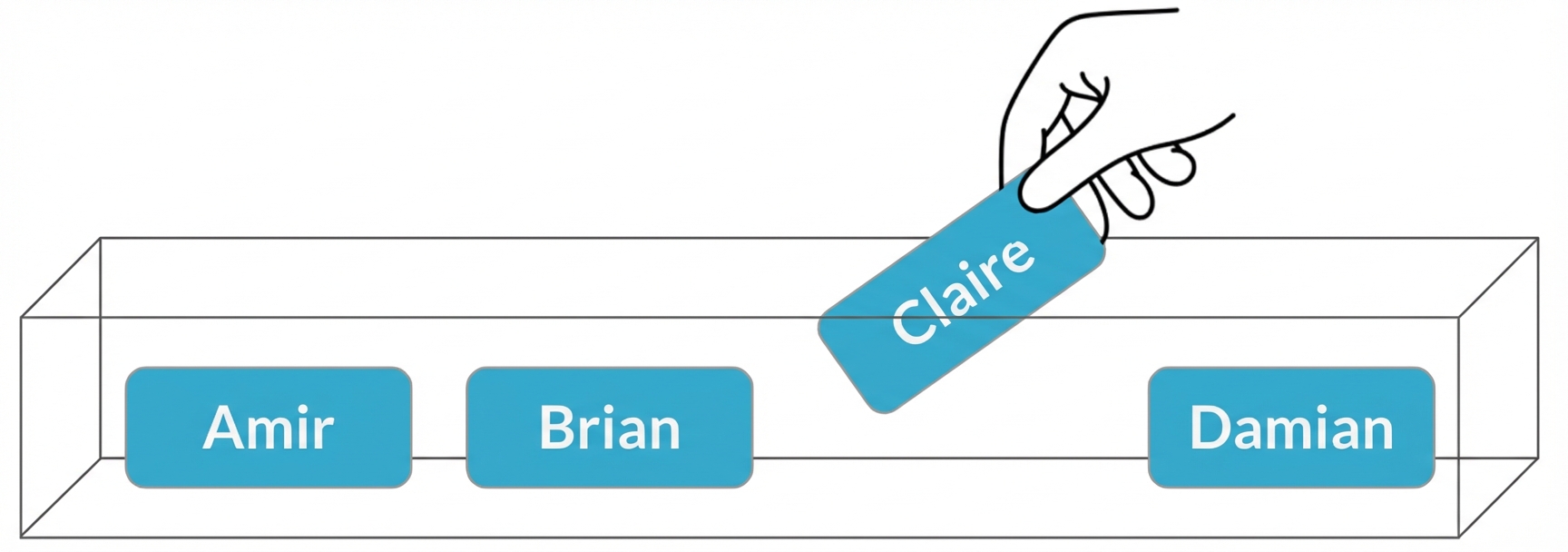
Auswahl von Vertrieblern
Auswahl von Vertrieblern

$$P(\text{Brian}) = \frac{1}{4} = 25\%$$
Stichproben aus einem DataFrame
sales_counts
name n_sales
1 Amir 178
2 Brian 126
3 Claire 75
4 Damian 69
sales_counts %>%
sample_n(1)
name n_sales
1 Brian 126
sales_counts %>%
sample_n(1)
name n_sales
1 Claire 75
Setzen eines Zufalls-Seed
set.seed(5)sales_counts %>% sample_n(1)
name n_sales
1 Brian 126
set.seed(5)sales_counts %>% sample_n(1)
name n_sales
1 Brian 126
Ein zweites Meeting
Stichproben ohne Zurücklegen

Ein zweites Meeting
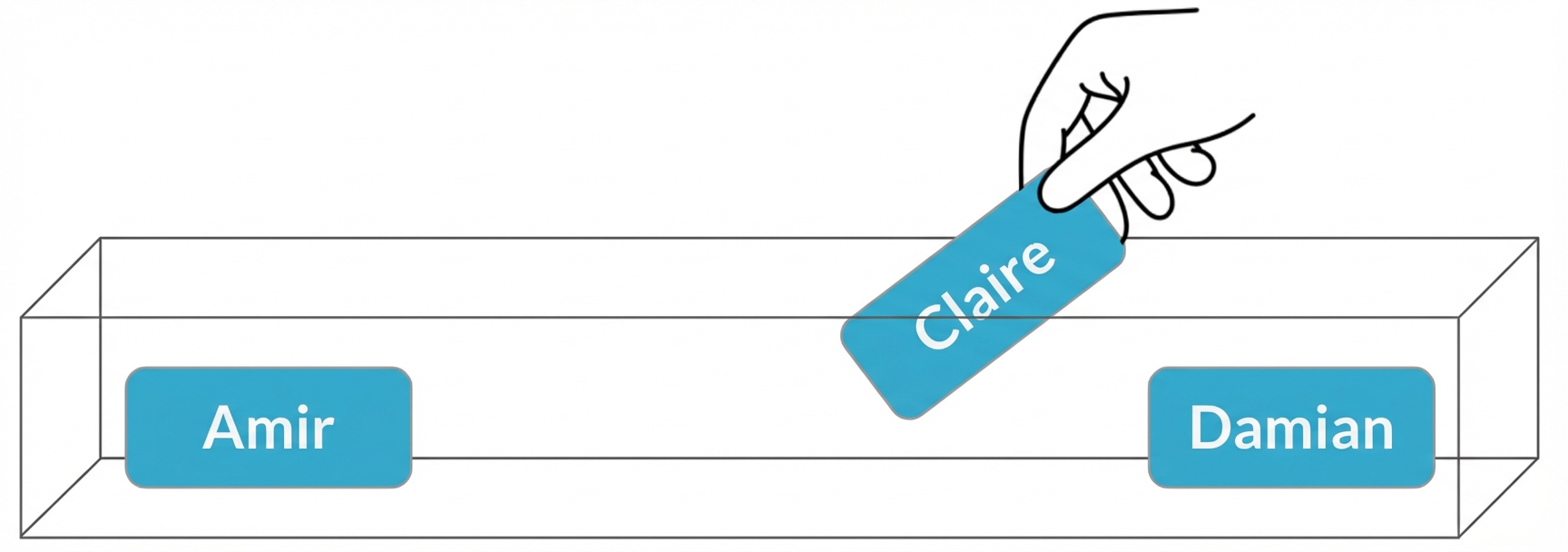
$$P(\text{Claire}) = \frac{1}{3} = 33\%$$
Zweimalige Stichprobe in R
sales_counts %>%
sample_n(2)
name n_sales
1 Brian 126
2 Claire 75
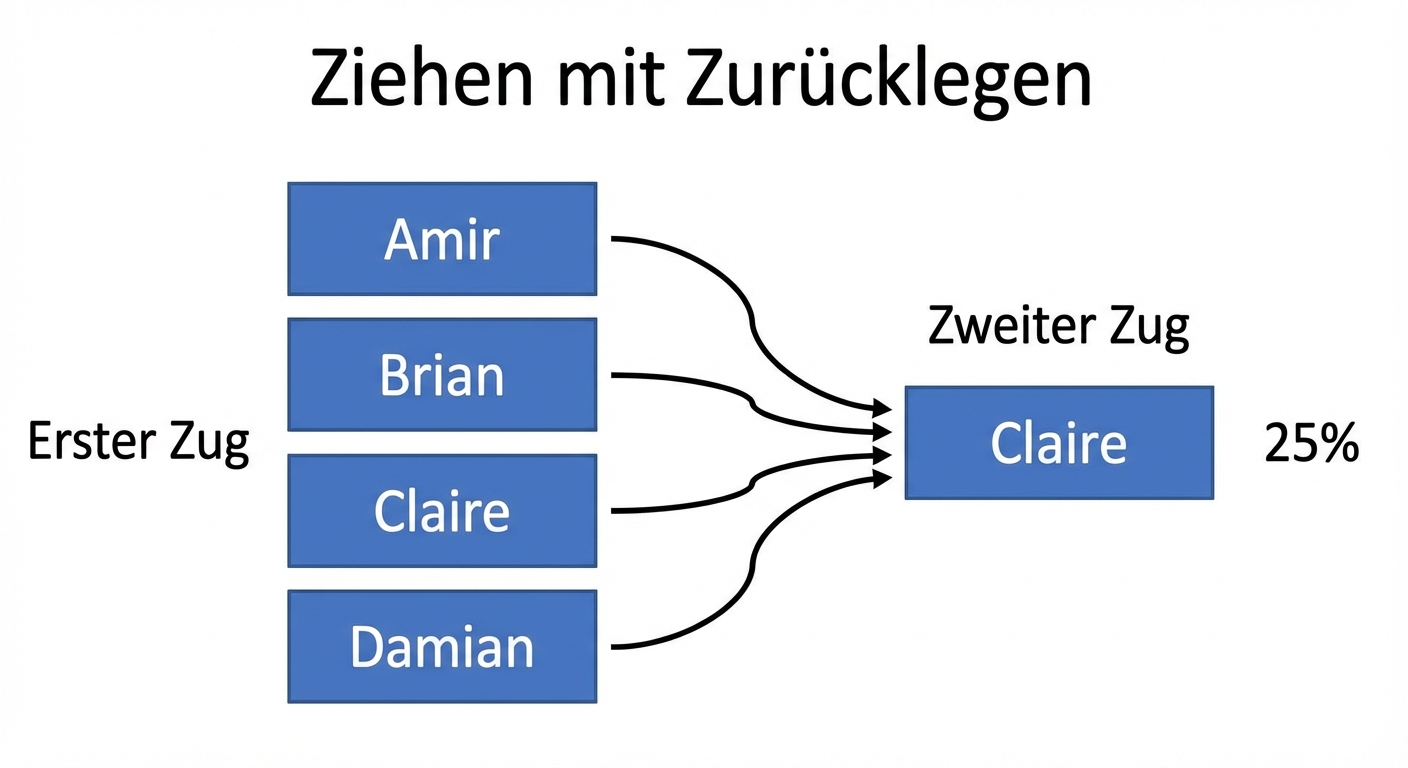
Stichproben mit Zurücklegen
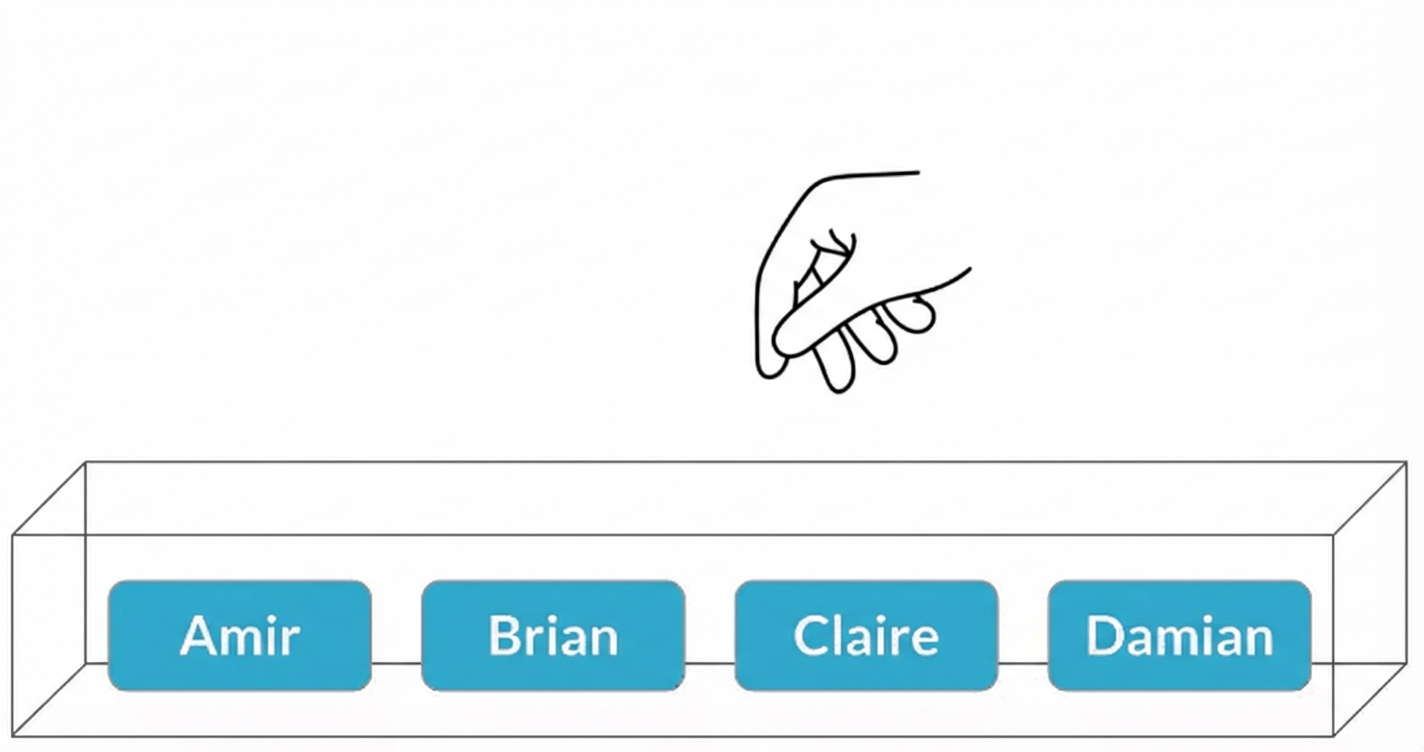
Stichproben mit Zurücklegen
$$P(\text{Claire}) = \frac{1}{4} = 25\%$$
Stichproben mit Zurücklegen in R
sales_counts %>%
sample_n(2, replace = TRUE)
name n_sales
1 Brian 126
2 Claire 75
5 Treffen:
sample(sales_team, 5, replace = TRUE)
name n_sales
1 Brian 126
2 Claire 75
3 Brian 126
4 Brian 126
5 Amir 178
Unabhängige Ereignisse
Zwei Ereignisse sind unabhängig, wenn die Wahrscheinlichkeit des zweiten Ereignisses nicht vom Ergebnis des ersten Ereignisses beeinflusst wird.

Unabhängige Ereignisse
Zwei Ereignisse sind unabhängig, wenn die Wahrscheinlichkeit des zweiten Ereignisses nicht vom Ergebnis des ersten Ereignisses beeinflusst wird.
Stichprobe mit Zurücklegen = jede Auswahl ist unabhängig
Abhängige Ereignisse
Zwei Ereignisse sind abhängig, wenn die Wahrscheinlichkeit des zweiten Ereignisses vom Ergebnis des ersten Ereignisses beeinflusst wird.

Abhängige Ereignisse
Zwei Ereignisse sind abhängig, wenn die Wahrscheinlichkeit des zweiten Ereignisses vom Ergebnis des ersten Ereignisses beeinflusst wird.
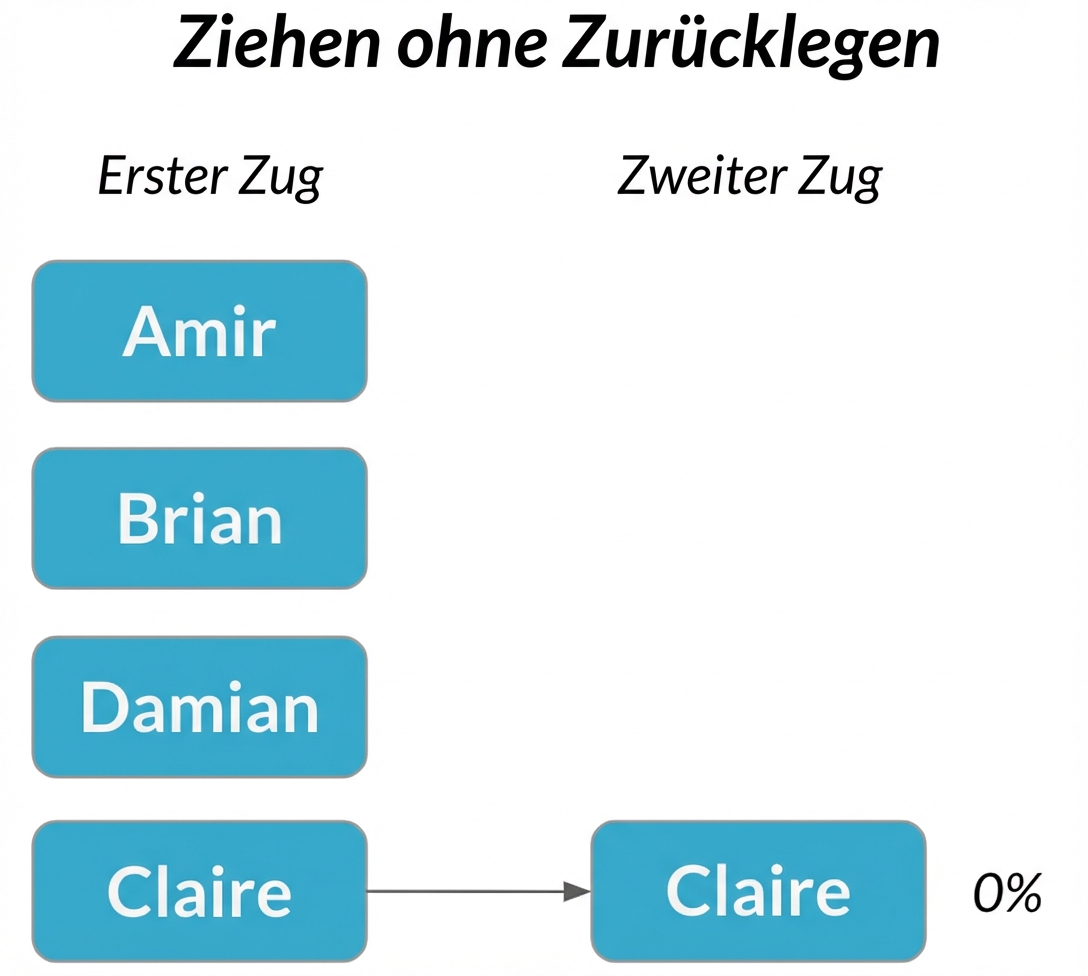
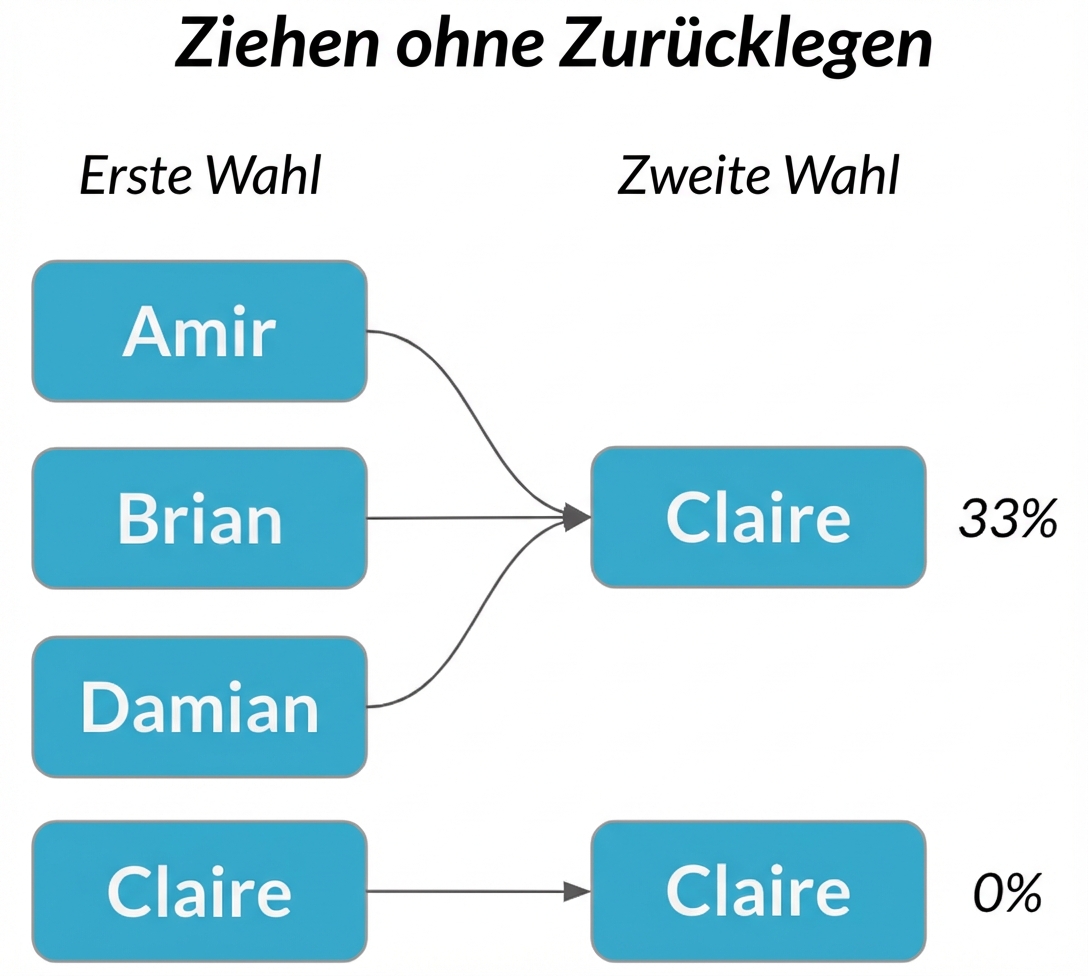
Abhängige Ereignisse
Zwei Ereignisse sind abhängig, wenn die Wahrscheinlichkeit des zweiten Ereignisses vom Ergebnis des ersten Ereignisses beeinflusst wird.
Stichprobe ohne Zurücklegen = jede Auswahl ist abhängig
Lass uns üben!
Einführung in die Statistik in R

