Transforming inputs before modeling

Supervised Learning in R: Regression

Nina Zumel and John Mount

Win-Vector LLC

Why To Transform Input Variables

  • Domain knowledge/synthetic variables
    • $Intelligence \sim \frac{mass.brain}{mass.body^{2/3}}$
Supervised Learning in R: Regression

Why To Transform Input Variables

  • Domain knowledge/synthetic variables
    • $Intelligence \sim \frac{mass.brain}{mass.body^{2/3}}$
  • Pragmatic reasons
    • Log transform to reduce dynamic range
    • Log transform because meaningful changes in variable are multiplicative
Supervised Learning in R: Regression

Why To Transform Input Variables

  • Domain knowledge/synthetic variables
    • $Intelligence \sim \frac{mass.brain}{mass.body^{2/3}}$
  • Pragmatic reasons
    • Log transform to reduce dynamic range
    • Log transform because meaningful changes in variable are multiplicative
    • $y$ approximately linear in $f(x)$ rather than in $x$
Supervised Learning in R: Regression

Example: Predicting Anxiety

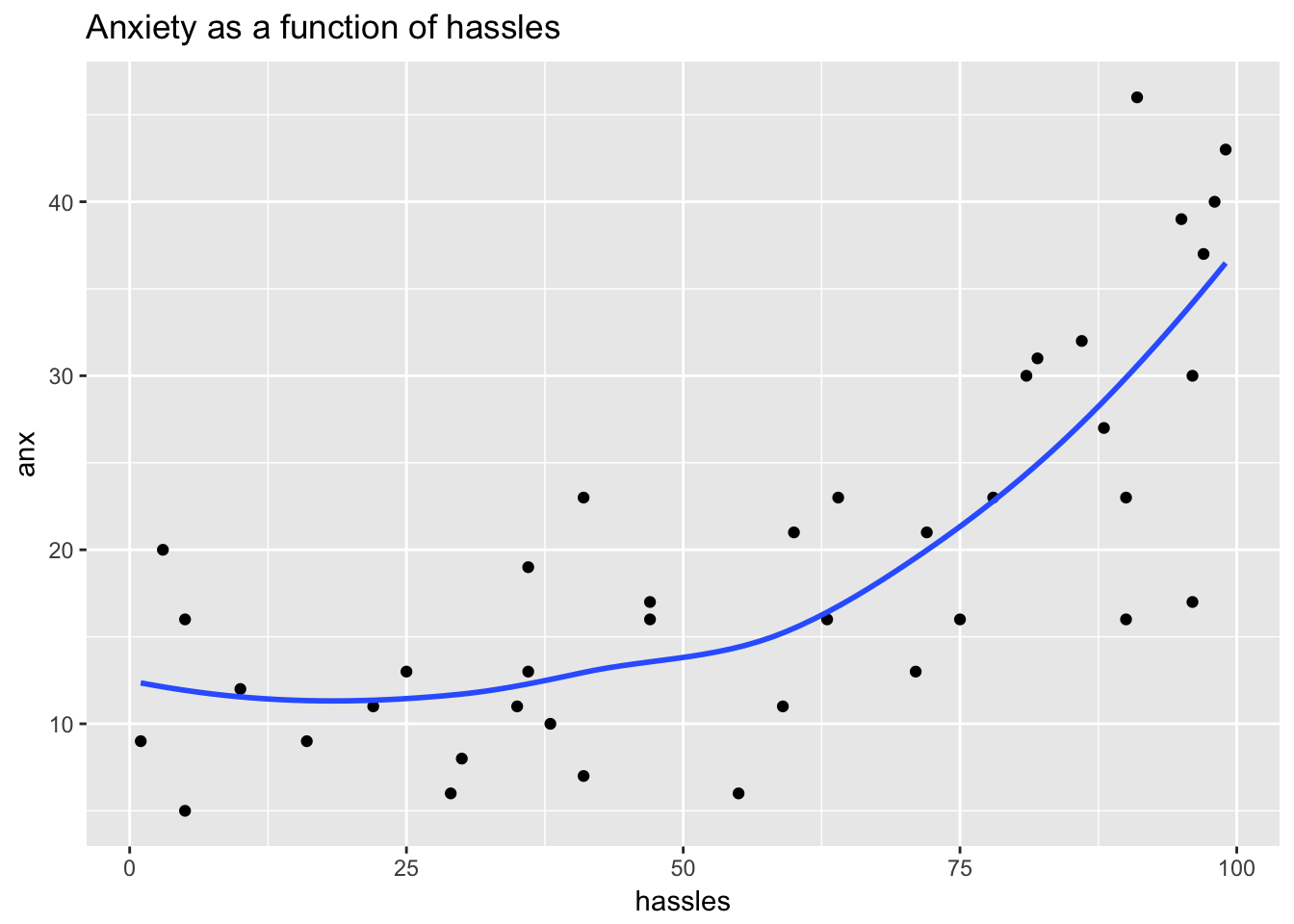
Supervised Learning in R: Regression

Transforming the hassles variable

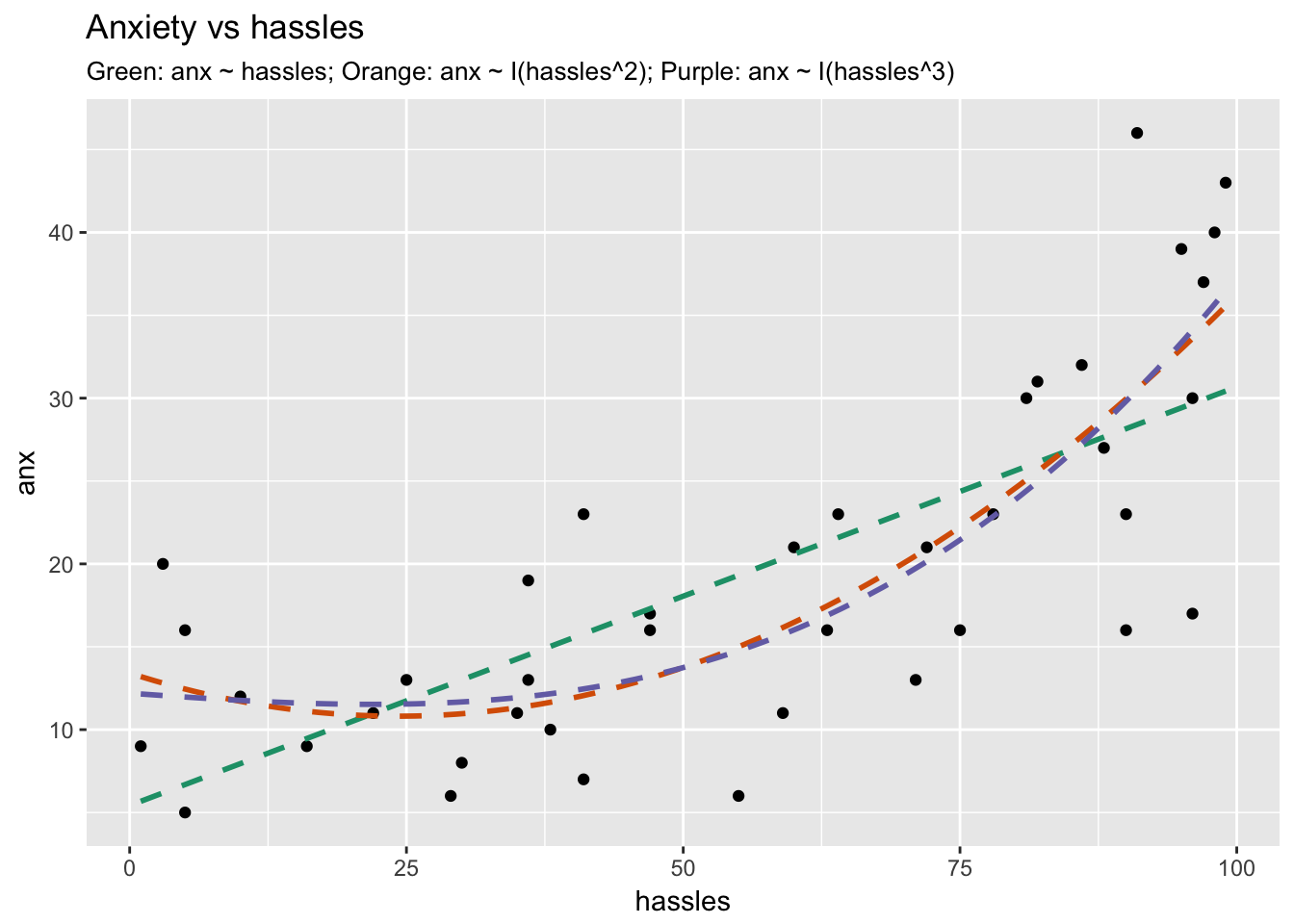
Supervised Learning in R: Regression

Different possible fits

Which is best?

  • anx ~ I(hassles^2)
  • anx ~ I(hassles^3)
  • anx ~ I(hassles^2) + I(hassles^3)
  • anx ~ exp(hassles)
  • ...

I(): treat an expression literally (not as an interaction)

Supervised Learning in R: Regression

Compare different models

Linear, Quadratic, and Cubic models

mod_lin <- lm(anx ~ hassles, hassleframe)
summary(mod_lin)$r.squared

0.5334847

mod_quad <- lm(anx ~ I(hassles^2), hassleframe)
summary(mod_quad)$r.squared

0.6241029

mod_tritic <- lm(anx ~ I(hassles^3), hassleframe)
summary(mod_tritic)$r.squared

0.6474421
Supervised Learning in R: Regression

Compare different models

Use cross-validation to evaluate the models

Model RMSE
Linear ($hassles$) 7.69
Quadratic ($hassles^2$) 6.89
Cubic ($hassles^3$) 6.70
Supervised Learning in R: Regression

Let's practice!

Supervised Learning in R: Regression

Preparing Video For Download...