Transforming the response before modeling
Supervised Learning in R: Regression

Nina Zumel and John Mount
Win-Vector, LLC
The Log Transform for Monetary Data
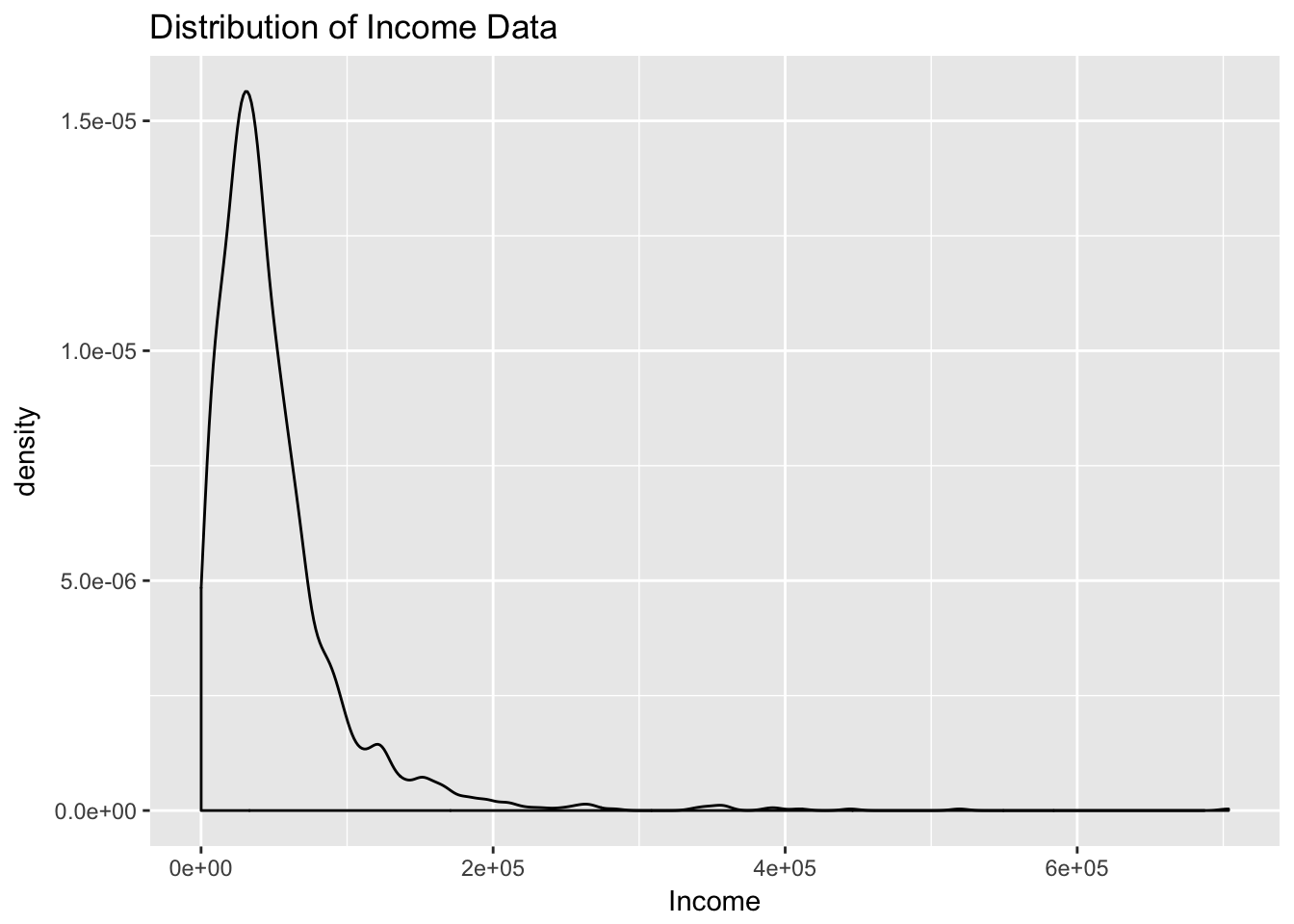
- Monetary values: lognormally distributed
- Long tail, wide dynamic range (60-700K)
Lognormal Distributions
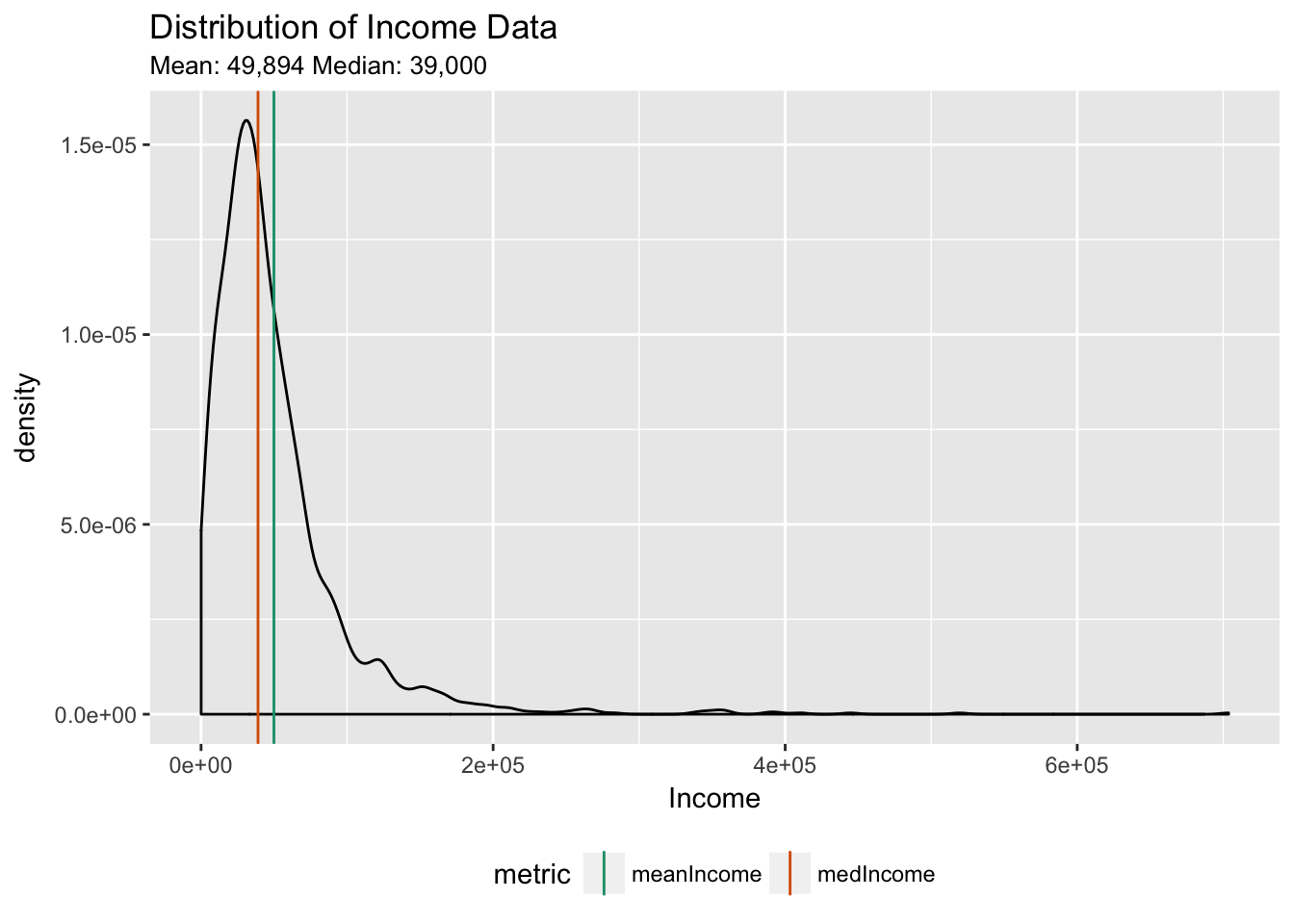
- mean > median (~ 50K vs 39K)
- Predicting the mean will overpredict typical values
Back to the Normal Distribution
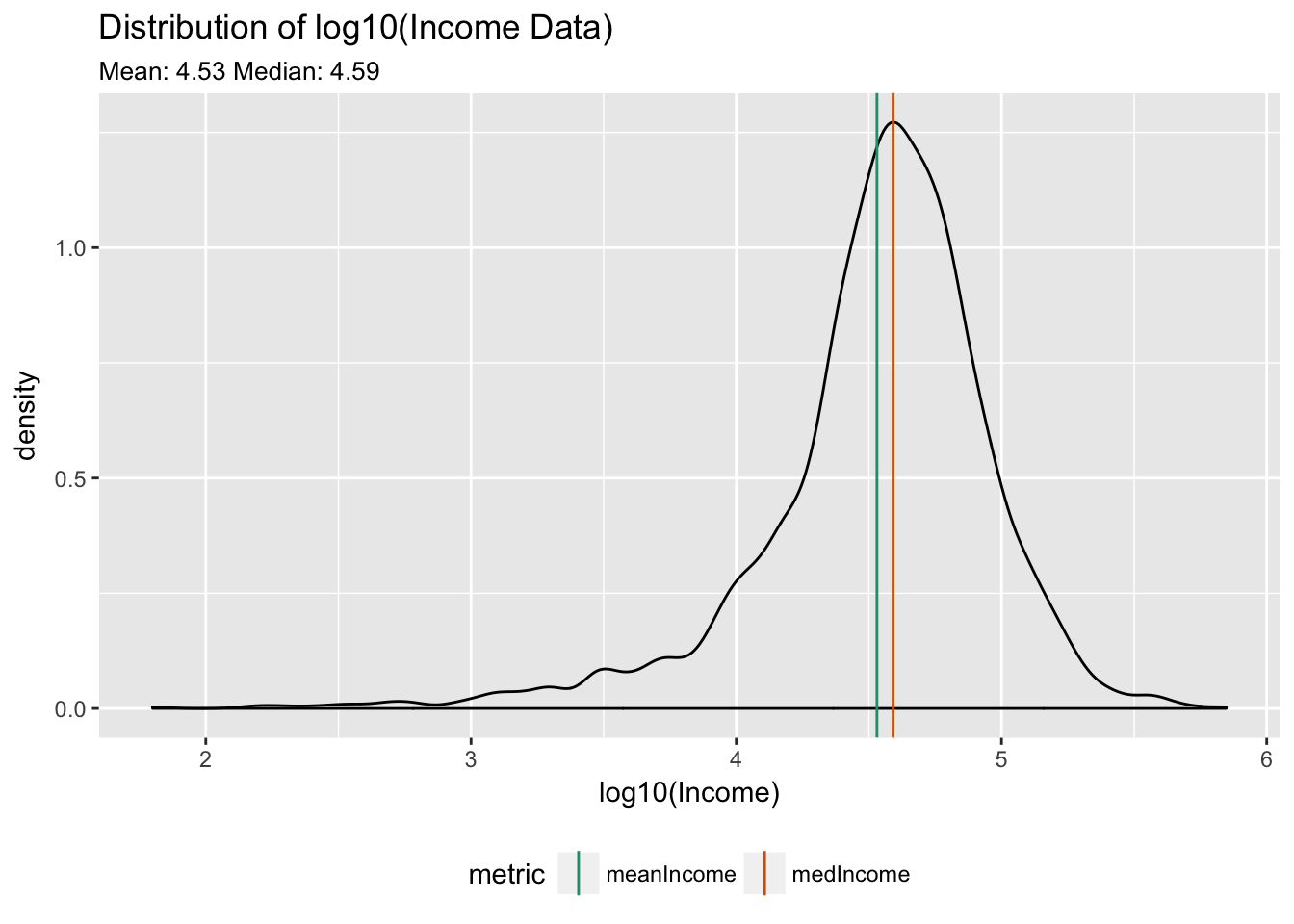
For a Normal Distribution:
- mean = median (here: 4.53 vs 4.59)
- more reasonable dynamic range (1.8 - 5.8)
The Procedure
- Log the outcome and fit a model
model <- lm(log(y) ~ x, data = train)
The Procedure
- Log the outcome and fit a model
model <- lm(log(y) ~ x, data = train) - Make the predictions in log space
logpred <- predict(model, data = test)
The Procedure
- Log the outcome and fit a model
model <- lm(log(y) ~ x, data = train) - Make the predictions in log space
logpred <- predict(model, data = test) - Transform the predictions to outcome space
pred <- exp(logpred)
Predicting Log-transformed Outcomes: Multiplicative Error
$log(a) + log(b) = log(ab)$
$log(a) - log(b) = log(a/b)$
- Multiplicative error: $pred/y$
- Relative error: $(pred - y)/y = \frac{pred}{y} - 1$
Reducing multiplicative error reduces relative error.
Root Mean Squared Relative Error
RMS-relative error = $\sqrt{ \overline{ (\frac{pred-y}{y})^2 }}$
- Predicting log-outcome reduces RMS-relative error
- But the model will often have larger RMSE
Example: Model Income Directly
modIncome <- lm(Income ~ AFQT + Educ, data = train)
AFQT: Score on proficiency test 25 years before surveyEduc: Years of education to time of surveyIncome: Income at time of survey
Model Performance
test %>%
+ mutate(pred = predict(modIncome, newdata = test),
+ err = pred - Income) %>%
+ summarize(rmse = sqrt(mean(err^2)),
+ rms.relerr = sqrt(mean((err/Income)^2)))
| RMSE | RMS-relative error |
|---|---|
| 36,819.39 | 3.295189 |
Model log(Income)
modLogIncome <- lm(log(Income) ~ AFQT + Educ, data = train)
Model Performance
test %>%
+ mutate(predlog = predict(modLogIncome, newdata = test),
+ pred = exp(predlog),
+ err = pred - Income) %>%
+ summarize(rmse = sqrt(mean(err^2)),
+ rms.relerr = sqrt(mean((err/Income)^2)))
| RMSE | RMS-relative error |
|---|---|
| 38,906.61 | 2.276865 |
Compare Errors
log(Income) model: smaller RMS-relative error, larger RMSE
| Model | RMSE | RMS-relative error |
|---|---|---|
On Income |
36,819.39 | 3.295189 |
On log(Income) |
38,906.61 | 2.276865 |
Let's practice!
Supervised Learning in R: Regression

