GAM to learn non-linear transformations

Supervised Learning in R: Regression

Nina Zumel and John Mount

Win-Vector, LLC

Generalized Additive Models (GAMs)

$$ y \sim b0 + s1(x1) + s2(x2) + .... $$

Supervised Learning in R: Regression

Learning Non-linear Relationships

Supervised Learning in R: Regression

gam() in the mgcv package

gam(formula, family, data)

family:

  • gaussian (default): "regular" regression
  • binomial: probabilities
  • poisson/quasipoisson: counts

Best for larger datasets

Supervised Learning in R: Regression

The s() function

anx ~ s(hassles)
  • s() designates that variable should be non-linear
  • Use s() with continuous variables
    • More than about 10 unique values
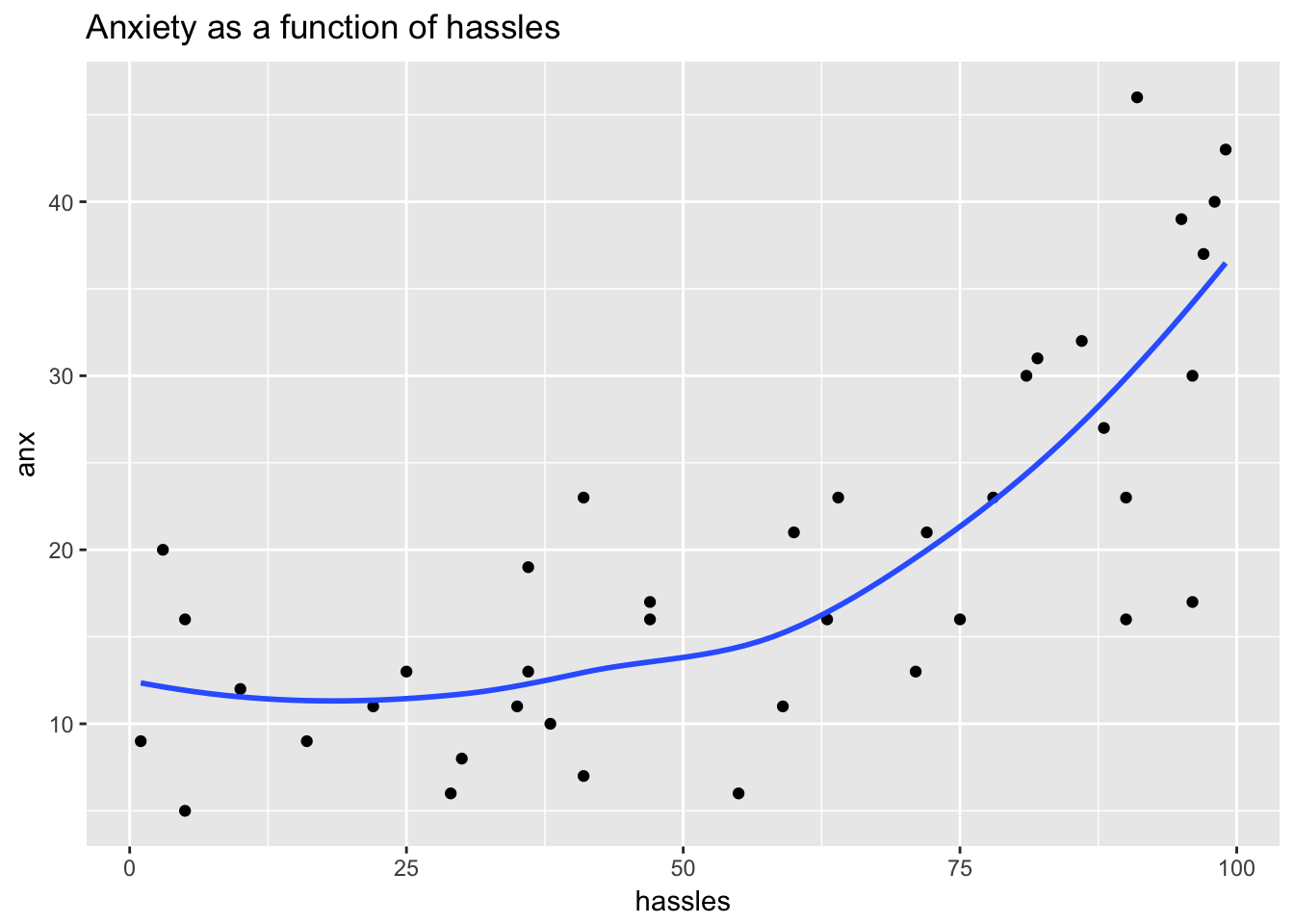
Supervised Learning in R: Regression

Revisit the hassles data

Supervised Learning in R: Regression

Revisit the hassles data

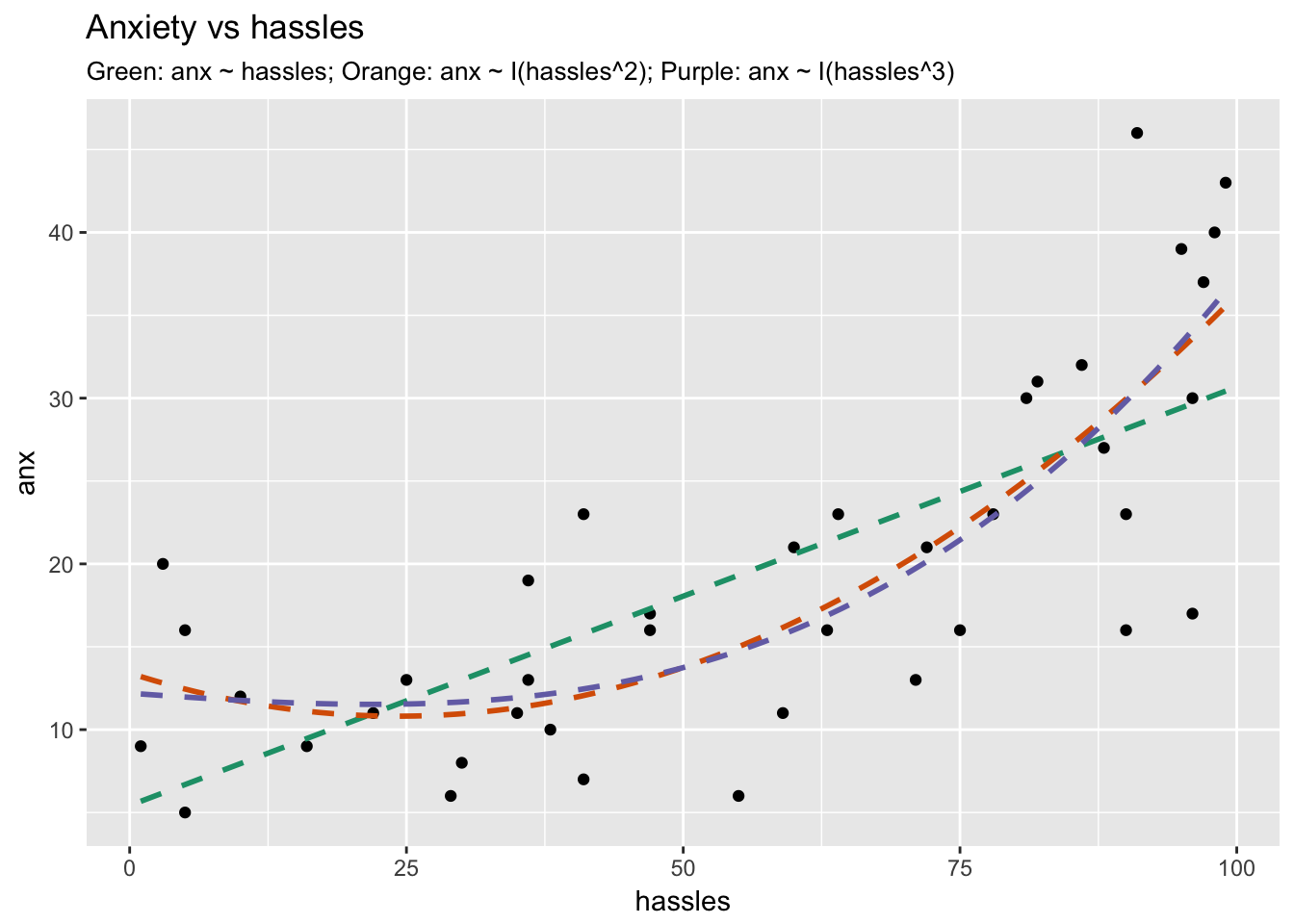
Model RMSE (cross-val) $R^2$ (training)
Linear ($hassles$) 7.69 0.53
Quadratic ($hassles^2$) 6.89 0.63
Cubic ($hassles^3$) 6.70 0.65
Supervised Learning in R: Regression

GAM of the hassles data

model <- gam(
  anx ~ s(hassles), 
  data = hassleframe, 
  family = gaussian
)

summary(model)

...

R-sq.(adj) =  0.619   Deviance explained = 64.1%
GCV = 49.132  Scale est. = 45.153    n = 40
Supervised Learning in R: Regression

Examining the Transformations

plot(model)

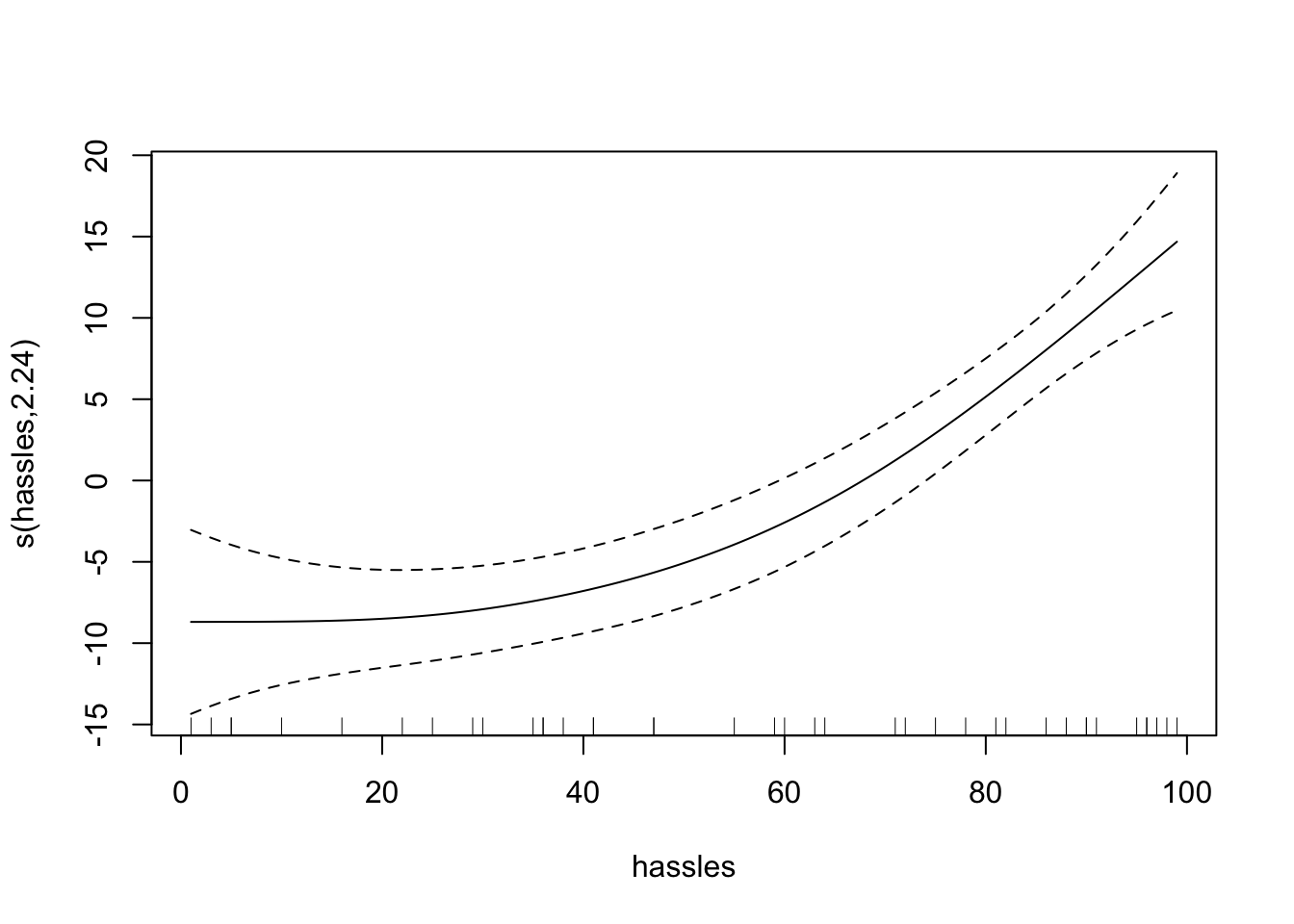
$y$ values: predict(model, type = "terms")

Supervised Learning in R: Regression

Predicting with the Model

predict(model, newdata = hassleframe, type = "response")

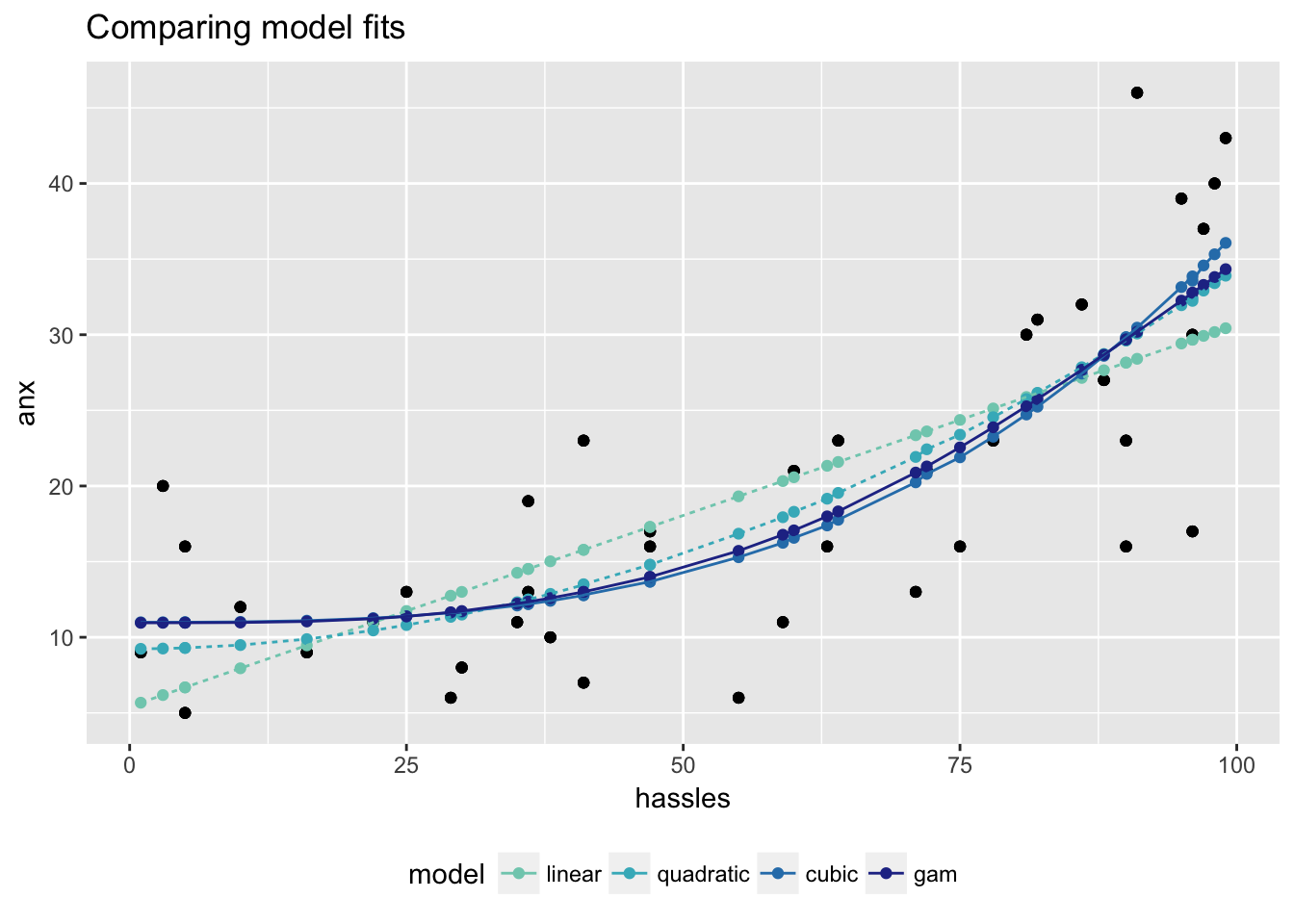
Supervised Learning in R: Regression

Comparing out-of-sample performance

Knowing the correct transformation is best, but GAM is useful when transformation isn't known

Model RMSE (cross-val) $R^2$ (training)
Linear ($hassles$) 7.69 0.53
Quadratic ($hassles^2$) 6.89 0.63
Cubic ($hassles^3$) 6.70 0.65
GAM 7.06 0.64
  • Small dataset $\rightarrow$ noisier GAM
Supervised Learning in R: Regression

Let's practice!

Supervised Learning in R: Regression

Preparing Video For Download...