Paired t-tests

Hypothesis Testing in R

Richie Cotton

Data Evangelist at DataCamp

US Republican presidents dataset

state	county	repub_percent_08	repub_percent_12
Alabama	Bullock	25.69	23.51
Alabama	Chilton	78.49	79.78
Alabama	Clay	73.09	72.31
Alabama	Cullman	81.85	84.16
Alabama	Escambia	63.89	62.46
Alabama	Fayette	73.93	76.19
Alabama	Franklin	68.83	69.68
...	...	...	...

500 rows; each row represents county-level votes in a presidential election.

¹ https://dataverse.harvard.edu/dataset.xhtml?persistentId=doi:10.7910/DVN/VOQCHQ

Hypotheses

Question: Was the percentage of votes given to the Republican candidate lower in 2008 compared to 2012?

$H_{0}$: $\mu_{2008} - \mu_{2012} = 0$

$H_{A}$: $\mu_{2008} - \mu_{2012} < 0$

Set $\alpha = 0.05$ significance level.

The data is paired, since each voter percentage refers to the same county.

From two samples to one

sample_data <- repub_votes_potus_08_12 %>% 
  mutate(diff = repub_percent_08 - repub_percent_12)

ggplot(sample_data, aes(x = diff)) +
  geom_histogram(binwidth = 1)

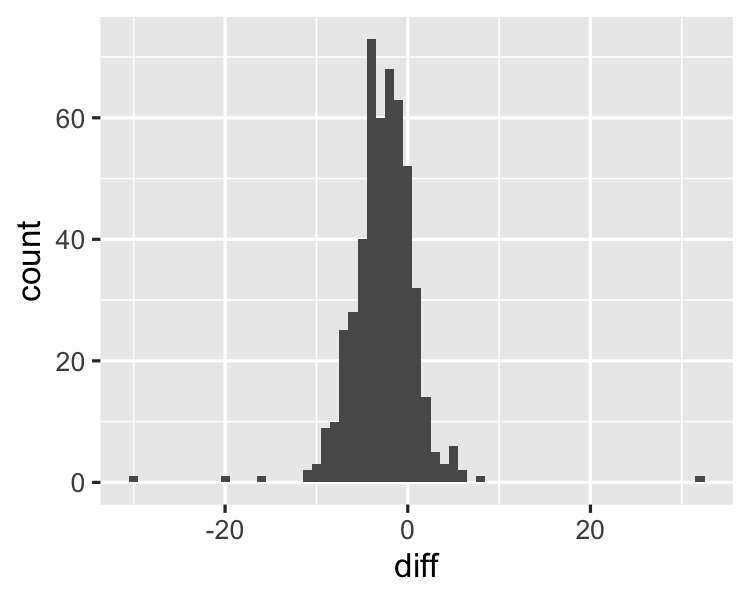
Histogram of the diff variable - most values are between -10 and 10 with some outliers.

Calculate sample statistics of the difference

sample_data %>% 
  summarize(xbar_diff = mean(diff))

  xbar_diff
1 -2.643027

Revised hypotheses

Old hypotheses

$H_{0}$: $\mu_{2008} - \mu_{2012} = 0$

$H_{A}$: $\mu_{2008} - \mu_{2012} < 0$

New hypotheses

$H_{0}$: $\mu_{\text{diff}} = 0$

$H_{A}$: $ \mu_{\text{diff}} < 0$

$t = \dfrac{\bar{x}_{\text{diff}} - \mu_{\text{diff}}}{\sqrt{\dfrac{s_{diff}^2}{n_{\text{diff}}}}}$

$df = n_{diff} - 1$

Calculating the p-value

n_diff <- nrow(sample_data)

s_diff <- sample_data %>% 
  summarize(sd_diff = sd(diff)) %>%
  pull(sd_diff)

t_stat <- (xbar_diff - 0) / sqrt(s_diff ^ 2 / n_diff)

-16.06374

degrees_of_freedom <- n_diff - 1

$t = \dfrac{\bar{x}_{\text{diff}} - \mu_{\text{diff}}}{\sqrt{\dfrac{s_{\text{diff}}^2}{n_{\text{diff}}}}}$

$df = n_{\text{diff}} - 1$

p_value <- pt(t_stat, df = degrees_of_freedom)

2.084965e-47

Testing differences between two means using t.test()

t.test(

  # Vector of differences
  sample_data$diff,

  # Choose between "two.sided", "less", "greater"
  alternative = "less",

  # Null hypothesis population parameter
  mu = 0

)

    One Sample t-test

data:  sample_data$diff
t = -16.064, df = 499, p-value < 2.2e-16
alternative hypothesis: true mean is less than 0
95 percent confidence interval:
     -Inf -2.37189
sample estimates:
mean of x 
-2.643027

t.test() with paired = TRUE

t.test(
  sample_data$repub_percent_08,
  sample_data$repub_percent_12,
  alternative = "less",
  mu = 0,
  paired = TRUE
)

    Paired t-test

data:  sample_data$repub_percent_08 and 
       sample_data$repub_percent_12
t = -16.064, df = 499, p-value < 2.2e-16
alternative hypothesis: true difference in means 
                        is less than 0
95 percent confidence interval:
     -Inf -2.37189
sample estimates:
mean of the differences 
              -2.643027

Unpaired t.test()

t.test(
  x = sample_data$repub_percent_08,
  y = sample_data$repub_percent_12,
  alternative = "less",
  mu = 0
)

Unpaired t-test has more chance of false negative error (less statistical power).

    Welch Two Sample t-test

data:  sample_data$repub_percent_08 and 
       sample_data$repub_percent_12
t = -2.8788, df = 992.76, p-value = 0.002039
alternative hypothesis: true difference in means
                        is less than 0
95 percent confidence interval:
      -Inf -1.131469
sample estimates:
mean of x mean of y 
 56.52034  59.16337

Let's practice!

Hypothesis Testing in R