Normal data
Experimental Design in Python

James Chapman
Curriculum Manager, DataCamp
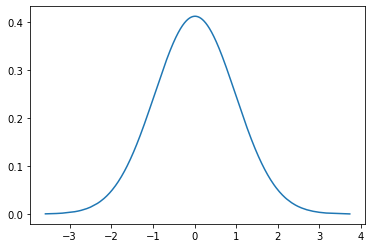
The normal distribution
- The familiar 'bell curve' shape
- Related to z-score work
$$ {z} = \frac{x-\mu}{\sigma}$$
- Mean = 0, std = 1
- 'How many standard deviations is this point from the mean?'
- 'What is the probability of obtaining this score?'
Normal data and statistical tests
- Required for parametric tests
- Nonparametric tests: don't assume normal data

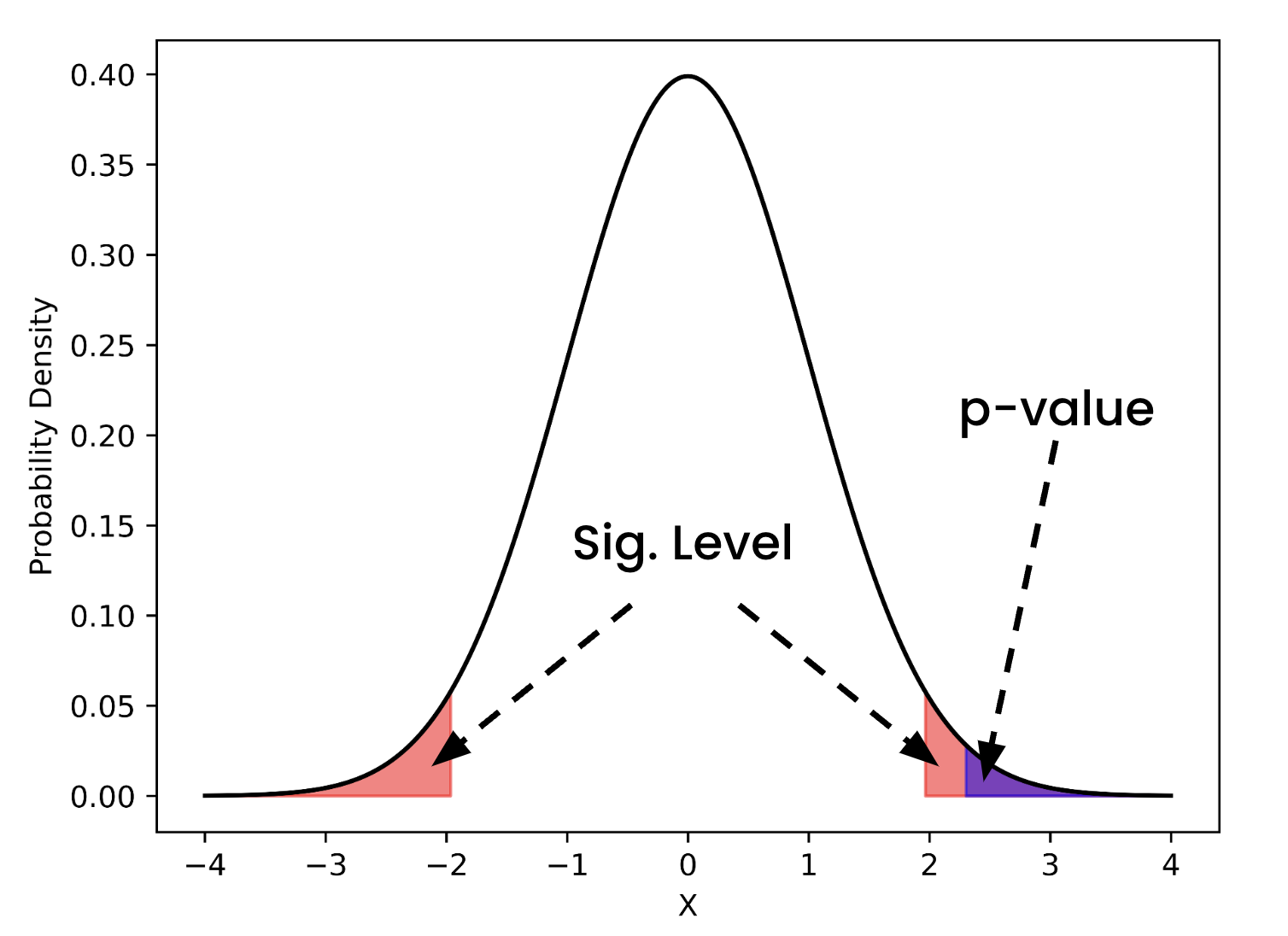
Normal, Z, and alpha
- Crucial link to significance level ($\alpha$)
- Compare p-value to $\alpha$
- Probability of a Type I error
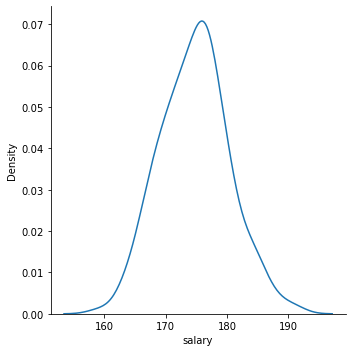
Visualizing normal data
sns.displot(data=salaries,
x='salary',
kind="kde")
plt.show()
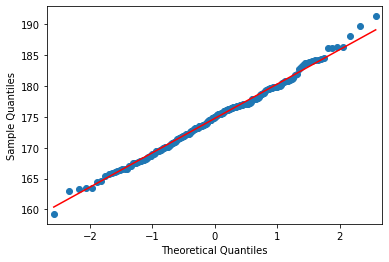
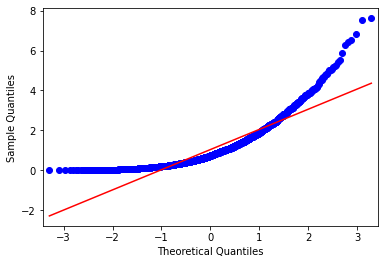
QQ plots
QQ plot: compare data to a particular distribution
from statsmodels.graphics.gofplots import qqplot
from scipy.stats.distributions import norm
qqplot(salaries['salary'],
line='s',
dist=norm)
plt.show()
- Ideal: dots hugging line
- Bad: bow out at ends
Tests for normality
- Shapiro-Wilk (good for smaller datasets)
- D'Agostino $K^2$ (uses kurtosis and skewness)
- Anderson-Darling (returns list of values)
$H_0$ = "Data is drawn from a Normal Distribution"
A Shapiro-Wilk test
from scipy.stats import shapiro alpha = 0.05stat, p = shapiro(salaries['salary']) print(f"p: {round(p,4)} test stat: {round(stat,4)}")
p: 0.8293 test stat: 0.9956
p>alpha- Fail to reject $H_0$ → likely normal
An Anderson-Darling test
from scipy.stats import anderson
result = anderson(x=salaries['salary'], dist="norm")
print(round(result.statistic,4))
print(result.significance_level)
print(result.critical_values)
0.2748
[15. 10. 5. 2.5 1. ]
[0.572 0.651 0.781 0.911 1.084]
0.2748<[0.572 0.651 0.781 0.911 1.084]- Fail to reject $H_0$ → likely normal
Let's practice!
Experimental Design in Python

