Conceptos básicos de la regresión lineal
Aprendizaje supervisado con scikit-learn

George Boorman
Core Curriculum Manager, DataCamp
Mecánica de regresión
$y = ax + b$
La regresión lineal simple utiliza una característica
$y$ = objetivo
$x$ = una característica
$a$, $b$ = parámetros/coeficientes del modelo - pendiente, intercepto
¿Cómo elegimos $a$ y $b$?
Se define una función de error para cualquier línea dada
Se elige la línea que minimice la función de error
Función de error = función de pérdida = función de coste
La función de pérdida
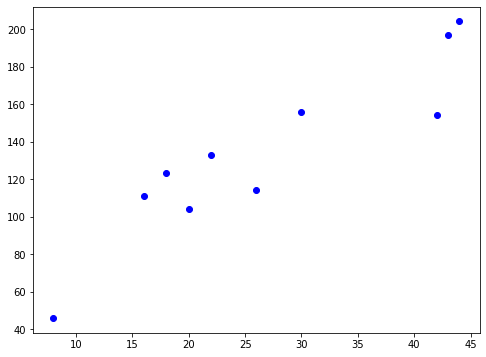
La función de pérdida
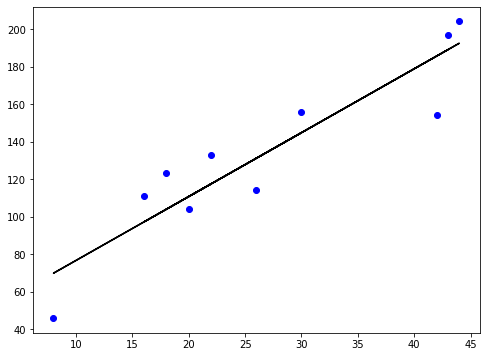
La función de pérdida
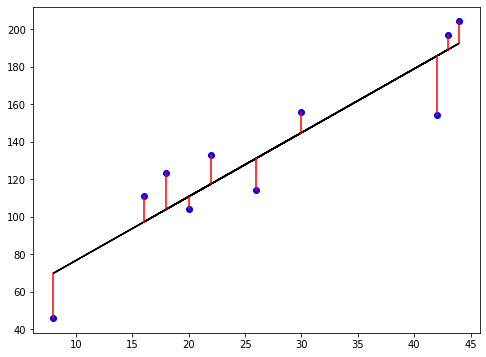
La función de pérdida
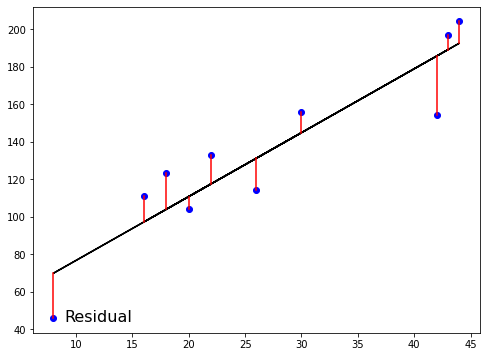
La función de pérdida
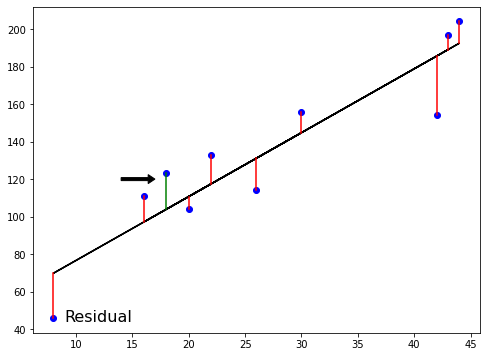
Mínimos cuadrados ordinarios
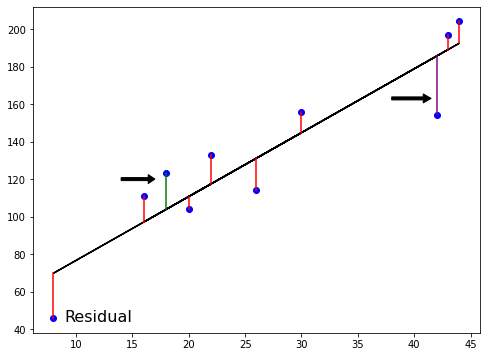
$RSS = $ $\displaystyle\sum_{i=1}^{n}(y_i-\hat{y_i})^2$
Mínimos cuadrados ordinarios (MCO): minimizar el RSS
Regresión lineal en dimensiones superiores
$$ y = a_{1}x_{1} + a_{2}x_{2} + b$$
- Para ajustar aquí un modelo de regresión lineal:
- Hay que especificar 3 variables: $ a_1,\ a_2,\ b $
- En dimensiones superiores:
- Se conoce como regresión múltiple
- Hay que especificar los coeficientes para cada característica y la variable $b$
$$ y = a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3} +... + a_{n}x_{n}+ b$$
- scikit-learn funciona exactamente igual:
- Se pasan dos matrices: características y objetivo
Regresión lineal utilizando todas las características
from sklearn.model_selection import train_test_split from sklearn.linear_model import LinearRegressionX_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3, random_state=42)reg_all = LinearRegression()reg_all.fit(X_train, y_train)y_pred = reg_all.predict(X_test)
R-cuadrado
$R^2$: cuantifica la varianza de los valores objetivo explicada por las características
- Los valores van de 0 a 1
$R^2$ alto:
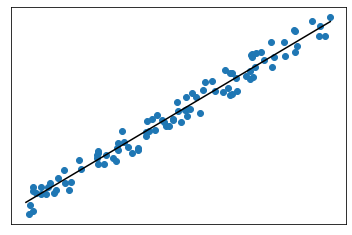
- $R^2$ bajo:
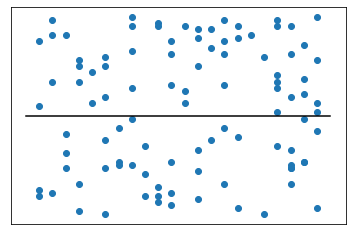
R-cuadrado en scikit-learn
reg_all.score(X_test, y_test)
0.356302876407827
Error cuadrático medio y raíz del error cuadrático medio
$MSE = $ $\displaystyle\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y_i})^2$
- El $MSE$ se mide en unidades objetivo, al cuadrado
$RMSE = $ $\sqrt{MSE}$
- El $RMSE$ se mide en las mismas unidades en la variable objetivo
RMSE en scikit-learn
from sklearn.metrics import root_mean_squared_errorroot_mean_squared_error(y_test, y_pred)
24.028109426907236
¡Vamos a practicar!
Aprendizaje supervisado con scikit-learn

