Regression zum Mittelwert

Einführung in Regression mit statsmodels in Python

Maarten Van den Broeck

Content Developer at DataCamp

Das Konzept

Antwortwert = angepasster Wert + Residuum
Das, was du erklärt hast + das, was du nicht erklären konntest
Residuen kommen wegen Problemen im Modell und zugrundeliegender Zufälligkeit vor.
Extreme Fälle basieren oft auf Zufall.
Die Regression zum Mittelwert bedeutet, dass extreme Fälle langfristig nicht bestehen bleiben.

Pearsons Vater-Sohn-Datensatz

1078 Vater-Sohn-Paare
Haben große Väter große Söhne?

father_height_cm	son_height_cm
165.2	151.8
160.7	160.6
165.0	160.9
167.0	159.5
155.3	163.3
...	...

¹ Adaptiert aus https://www.rdocumentation.org/packages/UsingR/topics/father.son

Streudiagramm

fig = plt.figure()

sns.scatterplot(x="father_height_cm",
                y="son_height_cm",
                data=father_son)

plt.axline(xy1=(150, 150),
           slope=1,
           linewidth=2,
           color="green")

plt.axis("equal")
plt.show()

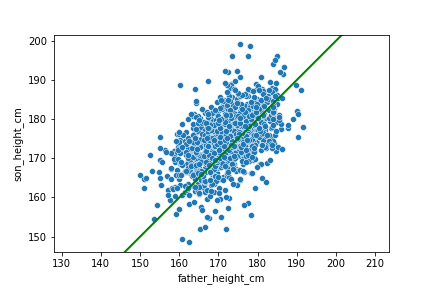
Ein Streudiagramm, das die Körpergröße der Söhne im Vergleich zur Körpergröße der Väter zeigt, mit einer Linie, wo Vater und Sohn gleich groß wären. Je größer die Väter werden, desto größer werden auch die Söhne.

Eine Regressionsgerade hinzufügen

fig = plt.figure()

sns.regplot(x="father_height_cm",
            y="son_height_cm",
            data=father_son,
            ci = None, 
            line_kws={"color": "black"})

plt.axline(xy1 = (150, 150),
           slope=1,
           linewidth=2,
           color="green")

plt.axis("equal")
plt.show()

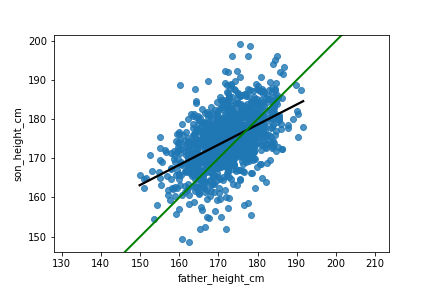
Das Streudiagramm der Körpergrößen der Söhne im Vergleich zu denen der Väter, mit einer linearen Trendlinie versehen. Die Trendlinie ist weniger steil als die Linie, bei der Väter und Söhne gleich groß wären.

Eine Regression durchführen

mdl_son_vs_father = ols("son_height_cm ~ father_height_cm",
                        data = father_son).fit()
print(mdl_son_vs_father.params)

Intercept           86.071975
father_height_cm     0.514093
dtype: float64

Vorhersagen treffen

really_tall_father = pd.DataFrame(
  {"father_height_cm": [190]})

mdl_son_vs_father.predict(
  really_tall_father)

183.7

really_short_father = pd.DataFrame(
  {"father_height_cm": [150]})

mdl_son_vs_father.predict(
  really_short_father)

163.2

Lass uns üben!

Einführung in Regression mit statsmodels in Python