Quantifizierung der Modellgüte

Einführung in Regression mit statsmodels in Python

Maarten Van den Broeck

Content Developer at DataCamp

Brassen- und Barschmodelle

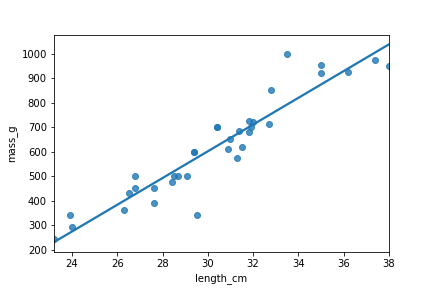
Brassen Das Streudiagramm der Degenfischgewichte im Vergleich zu ihrer Länge mit einer Trendlinie, das schon mal gezeigt wurde.

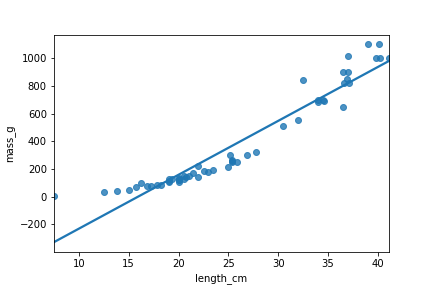
Barsche Das Streudiagramm der Gewichte von Barschen im Verhältnis zu ihrer Länge mit einer Trendlinie, das schon mal gezeigt wurde.

Bestimmtheitsmaß

Manchmal auch „r-squared“ oder „R-squared“ genannt.

Der Anteil der Varianz in der Antwortvariablen, der anhand der erklärenden Variablen vorhergesagt werden kann.

1 bedeutet eine perfekte Passform
0 bedeutet die schlechteste Passform

.summary()

Schau dir den Wert mit dem Titel „R-Quadrat“ an.

mdl_bream = ols("mass_g ~ length_cm", data=bream).fit()

print(mdl_bream.summary())

# Some lines of output omitted                          

                            OLS Regression Results                         
Dep. Variable:                 mass_g   R-squared:                       0.878
Model:                            OLS   Adj. R-squared:                  0.874
Method:                 Least Squares   F-statistic:                     237.6

.rsquared Attribut

print(mdl_bream.rsquared)

0.8780627095147174

Leidglich die Korrelation quadriert

coeff_determination = bream["length_cm"].corr(bream["mass_g"]) ** 2
print(coeff_determination)

0.8780627095147173

Standardfehler der Regression (RSE)

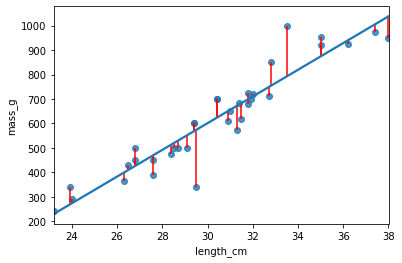
Reste des Streudiagramms von Masse und Länge der Brassen, wie zuvor gezeigt

Eine „typischer“ Distanz zwischen einer Vorhersage und einer beobachteten Reaktion
Hat die gleiche Einheit wie die Antwortvariable
MSE = RSE²

.mse_resid Attribut

mse = mdl_bream.mse_resid
print('mse: ', mse)

mse:  5498.555084973521

rse = np.sqrt(mse)
print("rse: ", rse)

rse:  74.15224261594197

Berechnung des RSE: Residuen quadriert

residuals_sq = mdl_bream.resid ** 2

print("residuals sq: 
", residuals_sq)

residuals sq: 
0      138.957118
1      260.758635
2     5126.992578
3     1318.919660
4      390.974309
    ...
30    2125.047026
31    6576.923291
32     206.259713
33     889.335096
34    7665.302003
Length: 35, dtype: float64

Berechnung des RSE: Summe der quadrierten Residuen

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

print("resid sum of sq :",
      resid_sum_of_sq)

resid sum of sq : 181452.31780412616

Berechnung des RSE: Freiheitsgrade

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

deg_freedom = len(bream.index) - 2

print("deg freedom: ", deg_freedom)

Die Freiheitsgrade sind gleich der Anzahl der Beobachtungen minus der Anzahl der Modellkoeffizienten.

deg freedom:  33

Berechnung des RSE: Quadratwurzel des Verhältnisses

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

deg_freedom = len(bream.index) - 2

rse = np.sqrt(resid_sum_of_sq/deg_freedom)

print("rse :", rse)

rse : 74.15224261594197

RSE interpretieren

mdl_bream hat einen RSE von 74.

Der Unterschied zwischen der vorhergesagten Brassenmasse und der tatsächlich gemessenen Brassenmasse ist normalerweise etwa 74 g.

Wurzel der mittleren Fehlerquadratsumme (RMSE)

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

deg_freedom = len(bream.index) - 2

rse = np.sqrt(resid_sum_of_sq/deg_freedom)

print("rse :", rse)

rse : 74.15224261594197

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

n_obs = len(bream.index)

rmse = np.sqrt(resid_sum_of_sq/n_obs)

print("rmse :", rmse)

rmse : 72.00244396727619

Lass uns üben!

Einführung in Regression mit statsmodels in Python