Anpassen (fitting) einer linearen Regression

Einführung in Regression mit statsmodels in Python

Maarten Van den Broeck

Content Developer at DataCamp

Zwei zentrale Eigenschaften von Geraden

Achsenabschnitt

Der $y$-Wert, für welchen $x$ gleich Null ist.

Steigung

Der Wert, um den der $y$-Wert zunimmt, wenn man $x$ um Eins erhöht.

Gleichung

$y = \text{Achsenabschnitt} + \text{Steigung} * x$

Den Achsenabschnitt schätzen

Ein Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle mit einer linearen Trendlinie. Die Zahlung steigt linear mit der Anzahl der Ansprüche.

Den Achsenabschnitt schätzen

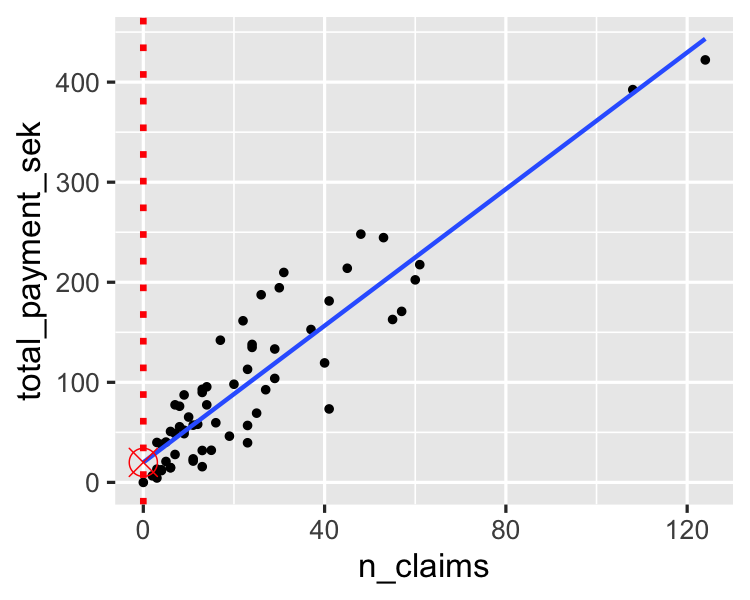
Das Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle, mit dem Punkt, wo die Trendlinie die y-Achse schneidet.

Den Achsenabschnitt schätzen

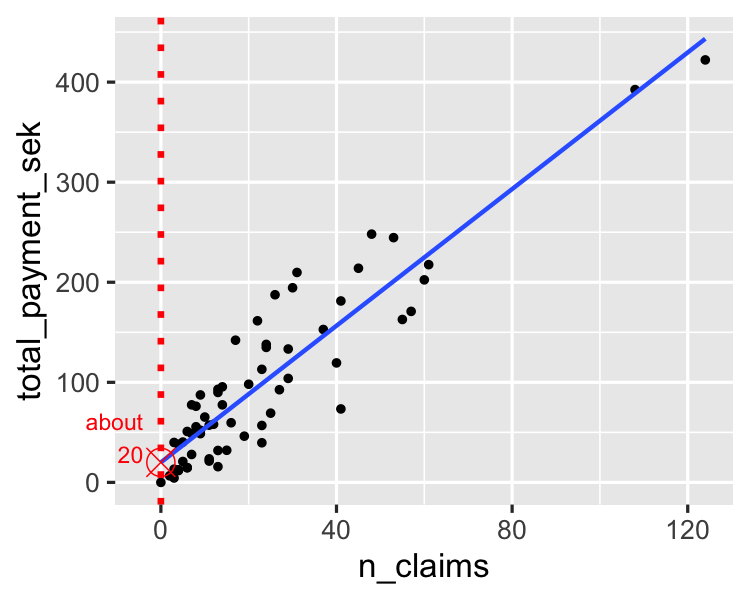
Das Streudiagramm der Gesamtzahlung im Vergleich zur Anzahl der Schadensfälle, mit dem Wert versehen, wenn die Anzahl der Schadensfälle null ist.

Die Steigung schätzen

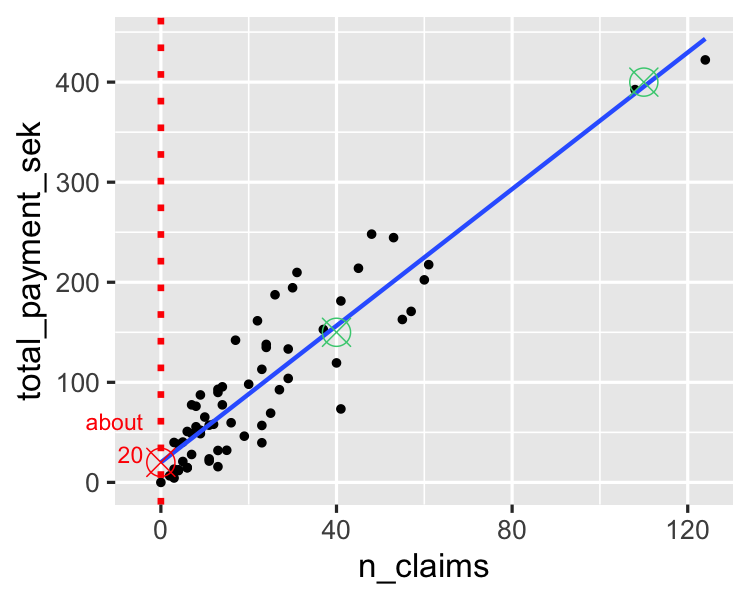
Das Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle, mit zwei Punkten auf der Trendlinie. Ein Punkt liegt bei 1500 Kronen und 40 Ansprüchen, ein anderer Punkt bei 3500 Kronen und 100 Ansprüchen.

Die Steigung schätzen

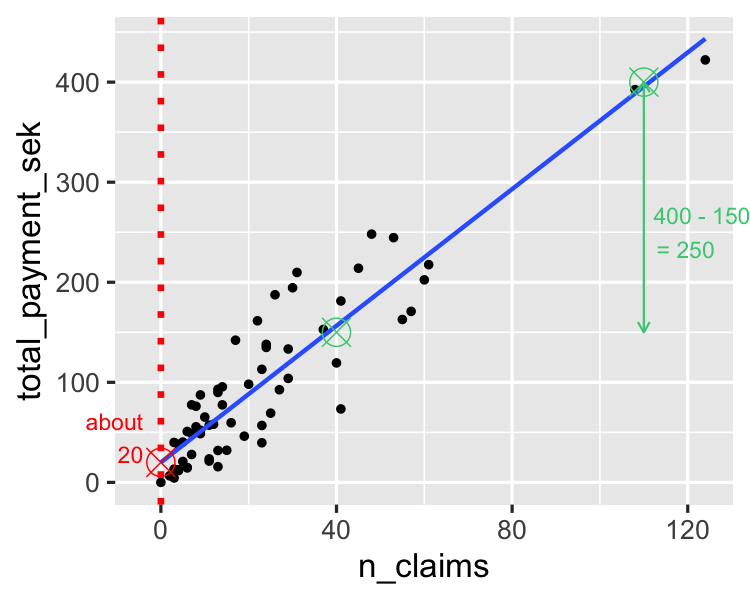
Das Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle, mit den Zahlungsunterschieden zwischen den beiden Punkten. 3500 Kronen minus 1500 Kronen sind 2000 Kronen.

Die Steigung schätzen

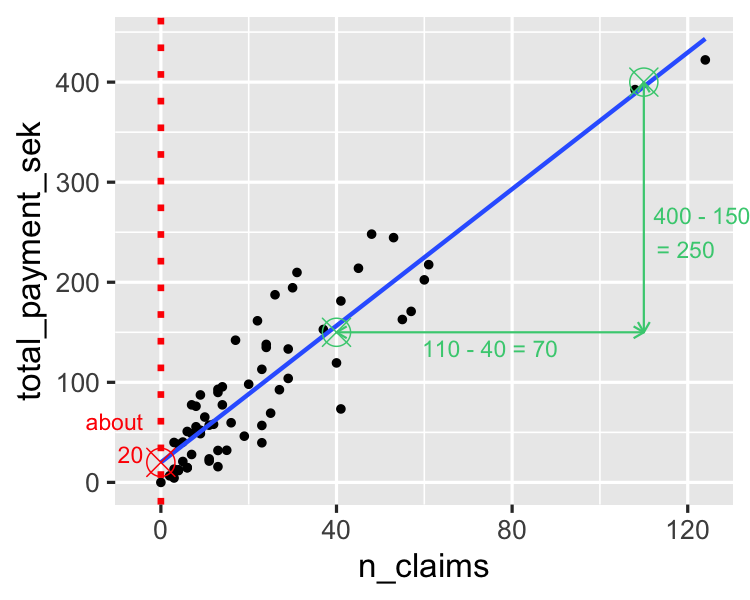
Das Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle, mit Anmerkungen zur Differenz in der Anzahl der Schadensfälle zwischen den beiden Punkten. 100 Ansprüche minus 40 Ansprüche sind 60 Ansprüche.

Die Steigung schätzen

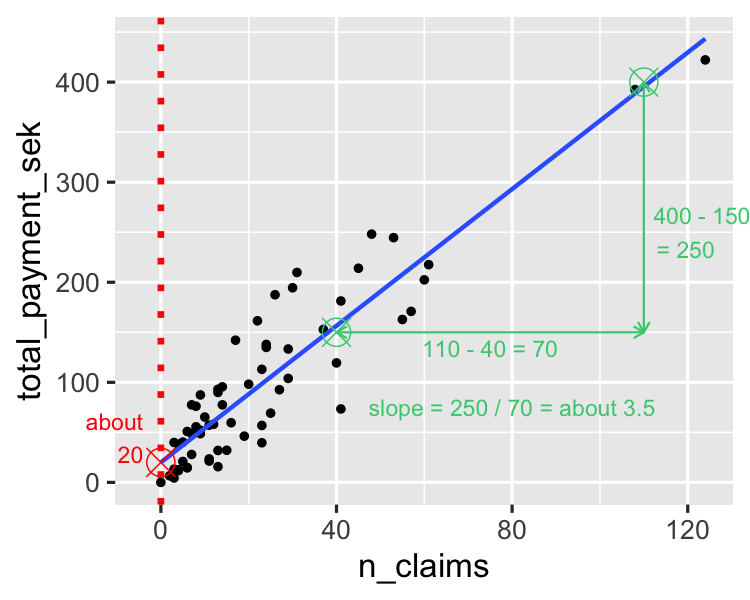
Das Streudiagramm der Gesamtzahlungen im Vergleich zur Anzahl der Schadensfälle, mit Anmerkungen zum Verhältnis von Differenz und Zahlung sowie zur Differenz in der Anzahl der Schadensfälle. 2000 geteilt durch 60 ist ungefähr 33.

Ein Modell ausführen

from statsmodels.formula.api import ols

mdl_payment_vs_claims = ols("total_payment_sek ~ n_claims",
                            data=swedish_motor_insurance)


mdl_payment_vs_claims = mdl_payment_vs_claims.fit()

print(mdl_payment_vs_claims.params)

Intercept    19.994486
n_claims      3.413824
dtype: float64

Interpretation der Modellkoeffizienten

Intercept    19.994486
n_claims      3.413824
dtype: float64

Gleichung

$\text{total\_payment\_sek} = 19.99 + 3.41 * \text{n\_claims}$

Lass uns üben!

Einführung in Regression mit statsmodels in Python