Quantifizierung der logistischen Regressionsgüte

Einführung in Regression mit statsmodels in Python

Maarten Van den Broeck

Content Developer at DataCamp

Die vier Ergebnisse

	als „falsch“ vorhergesagt	als „wahr“ vorhergesagt
tatsächlich falsch	korrekt	falsch positiv
tatsächlich wahr	falsch negativ	korrekt

Konfusionsmatrix: Anzahl der Ergebnisse

actual_response = churn["has_churned"]

predicted_response = np.round(mdl_recency.predict())

outcomes = pd.DataFrame({"actual_response": actual_response,
                         "predicted_response": predicted_response})

print(outcomes.value_counts(sort=False))

actual_response  predicted_response
0                0.0                   141
                 1.0                    59
1                0.0                   111
                 1.0                    89

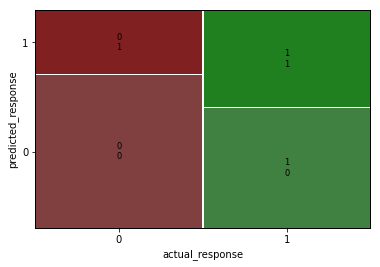
Visualisierung der Konfusionsmatrix

conf_matrix = mdl_recency.pred_table()

print(conf_matrix)

[[141.              59.]
 [111.              89.]]

tatsächlich negativ	falsch positiv
falsch negativ	tatsächlich positiv

from statsmodels.graphics.mosaicplot
import mosaic

mosaic(conf_matrix)

Ein Mosaikdiagramm der Ergebnisse des Churn-versus-Recency-Modells. Es gibt jeweils 200 Beobachtungen für echte Abwanderungen und echte Nicht-Abwanderungen, sodass jede Spalte gleich breit ist.

Genauigkeit

Genauigkeit ist der Anteil der korrekten Vorhersagen.

$$ \text{accuracy} = \frac{TN + TP}{TN + FN + FP + TP} $$

 [[141.,  59.],
  [111.,  89.]]

TN = conf_matrix[0,0]
TP = conf_matrix[1,1]
FN = conf_matrix[1,0]
FP = conf_matrix[0,1]

acc = (TN + TP) / (TN + TP + FN + FP)
print(acc)

0.575

Empfindlichkeit

Sensitivität ist der Anteil der tatsächlich positiven Ergebnisse.

$$ \text{sensitivity} = \frac{TP}{FN + TP} $$

 [[141.,  59.],
  [111.,  89.]]

TN = conf_matrix[0,0]
TP = conf_matrix[1,1]
FN = conf_matrix[1,0]
FP = conf_matrix[0,1]

sens = TP / (FN + TP)
print(sens)

0.445

Spezifität

Spezifität ist der Anteil der tatsächlichen Negativbefunde.

$$ \text{specificity} = \frac{TN}{TN + FP} $$

 [[141.,  59.],
  [111.,  89.]]

TN = conf_matrix[0,0]
TP = conf_matrix[1,1]
FN = conf_matrix[1,0]
FP = conf_matrix[0,1]

spec = TN / (TN + FP)
print(spec)

0.705

Lass uns üben!

Einführung in Regression mit statsmodels in Python