Prognosen und Odds Ratios

Einführung in Regression mit statsmodels in Python

Maarten Van den Broeck

Content Developer at DataCamp

Die Vorhersagen von regplot()

sns.regplot(x="time_since_last_purchase",
            y="has_churned",
            data=churn,
            ci=None,
            logistic=True)

plt.show()

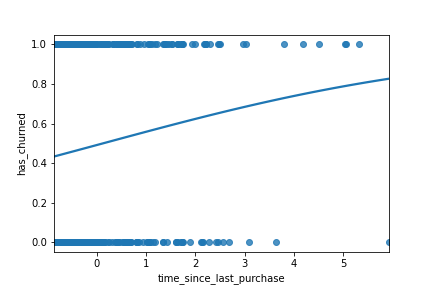
Ein Streudiagramm der Abwanderungsrate im Vergleich zur Zeit seit dem letzten Kauf, mit einer logistischen Trendlinie.

Vorhersagen treffen

mdl_recency = logit("has_churned ~ time_since_last_purchase",
                    data = churn).fit()


explanatory_data = pd.DataFrame(
  {"time_since_last_purchase": np.arange(-1, 6.25, 0.25)})


prediction_data = explanatory_data.assign(
    has_churned = mdl_recency.predict(explanatory_data))

Punktvorhersagen hinzufügen

sns.regplot(x="time_since_last_purchase",
            y="has_churned",
            data=churn,
            ci=None,
            logistic=True)

sns.scatterplot(x="time_since_last_purchase",
                y="has_churned",
                data=prediction_data,
                color="red")

plt.show()

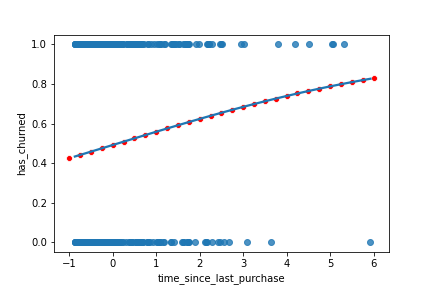
Das Streudiagramm der Abwanderung im Vergleich zur Zeit seit dem letzten Kauf, mit einer logistischen Trendlinie. Die Grafik zeigt die Ergebnisse von predict(), die genau der Trendlinie folgen.

Das wahrscheinlichste Ergebnis bekommen

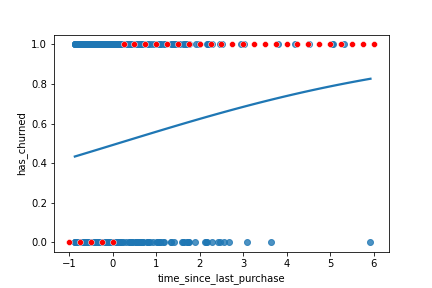
prediction_data = explanatory_data.assign(
    has_churned = mdl_recency.predict(explanatory_data))

prediction_data["most_likely_outcome"] = np.round(prediction_data["has_churned"])

Das wahrscheinlichste Ergebnis visualisieren

sns.regplot(x="time_since_last_purchase",
            y="has_churned",
            data=churn,
            ci=None,
            logistic=True)

sns.scatterplot(x="time_since_last_purchase",
                y="most_likely_outcome",
                data=prediction_data,
                color="red")

plt.show()

Odds Ratios

Die Odds Ratio ist die Wahrscheinlichkeit, dass etwas passiert, geteilt durch die Wahrscheinlichkeit, dass es nicht passiert.

$$ \text{odds\_ratio} = \frac{\text{probability}}{(1 - \text{probability)}} $$

$$ \text{odds\_ratio} = \frac{0.25}{(1 - 0.25)} = \frac{1}{3} $$

Ein Liniendiagramm, das die Odds Ratio gegen die Wahrscheinlichkeit zeigt. Die Kurve steigt asymptotisch gegen unendlich, wenn die Wahrscheinlichkeit gegen eins geht.

Berechnung der Odds Ratio

prediction_data["odds_ratio"] = prediction_data["has_churned"] / 
                                (1 - prediction_data["has_churned"])

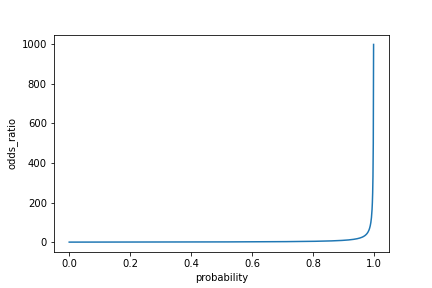
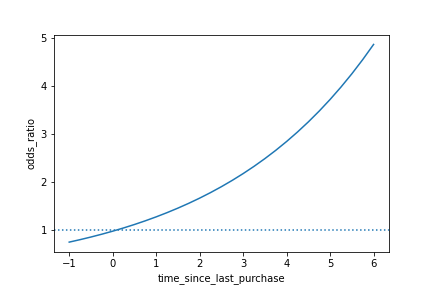
Visualisierung der Odds Ratio

sns.lineplot(x="time_since_last_purchase",
             y="odds_ratio",
             data=prediction_data)


plt.axhline(y=1,
            linestyle="dotted")


plt.show()

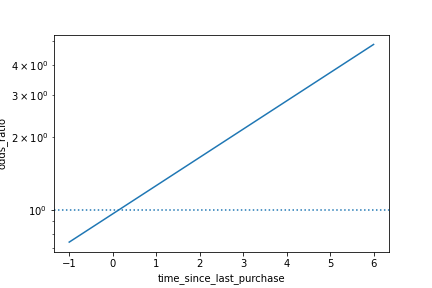
Visualisierung der Log-Odds-Ratio

sns.lineplot(x="time_since_last_purchase",
             y="odds_ratio",
             data=prediction_data)

plt.axhline(y=1,
            linestyle="dotted")

plt.yscale("log")

plt.show()

Das Liniendiagramm zeigt das Verhältnis der Wahrscheinlichkeiten im Vergleich zur Zeit seit dem letzten Kauf, mit einer Linie bei einem Verhältnis von eins. Die y-Achse hat 'ne logarithmische Skala, was dazu führt, dass die Odds-Ratio-Linie linear wird.

Log-Odds-Ratio berechnen

prediction_data["log_odds_ratio"] = np.log(prediction_data["odds_ratio"])

Alle Vorhersagen

time_since_last_prchs	has_churned	most_likely_rspns	odds_ratio	log_odds_ratio
0	0.491	0	0.966	-0.035
2	0.623	1	1.654	0.503
4	0.739	1	2.834	1.042
6	0.829	1	4.856	1.580
...	...	...	...	...

Skalen vergleichen

Skala	Sind Werte leicht zu verstehen?	Sind Veränderungen leicht zu verstehen?	Präzision?
Wahrscheinlichkeit	✔	✘	✔
Wahrscheinlichstes Ergebnis	✔✔	✔	✘
Odds Ratio	✔	✘	✔
Log odds ratio	✘	✔	✔

Lass uns üben!

Einführung in Regression mit statsmodels in Python