Binary Search Tree (BST)
Data Structures and Algorithms in Python

Miriam Antona
Software engineer
Definition
- Left subtree of a node:
- values less than the node itself
- Right subtree of a node:
- values greater than the node itself
- Left and right subtrees must be binary search trees
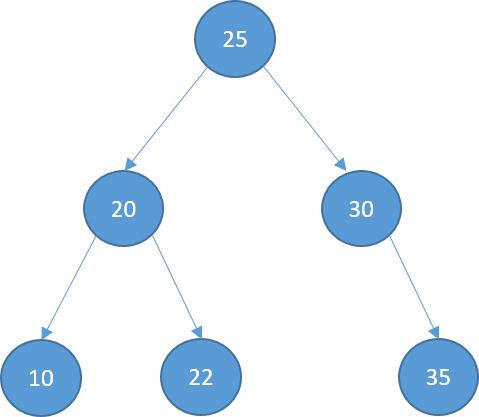
Implementation
class TreeNode:
def __init__(self, data, left=None, right=None):
self.data = data
self.left_child = left
self.right_child = right
class BinarySearchTree:
def __init__(self):
self.root = None
Searching
- Search for 72
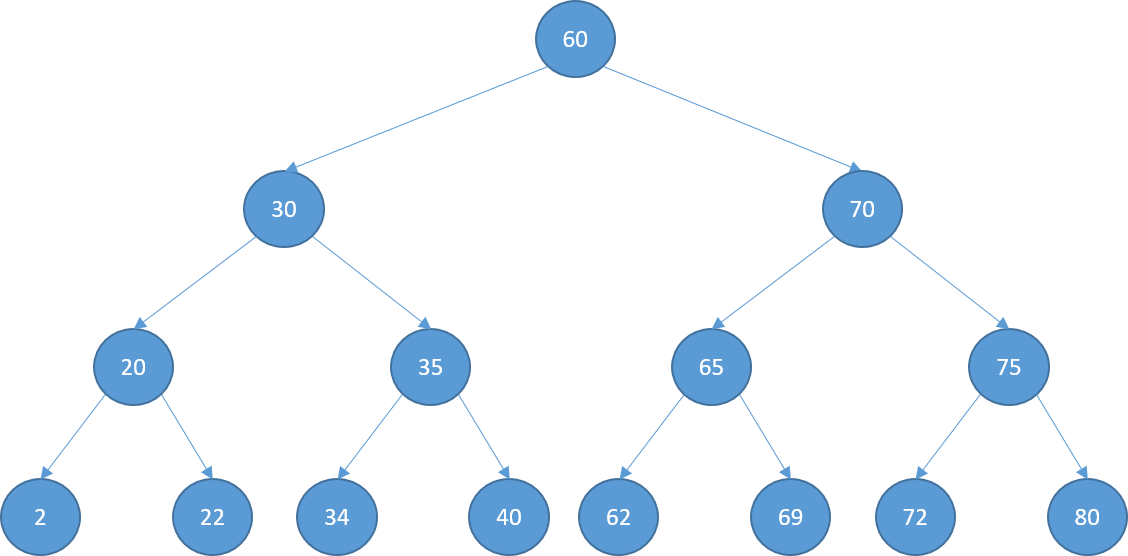
Searching
- Search for 72
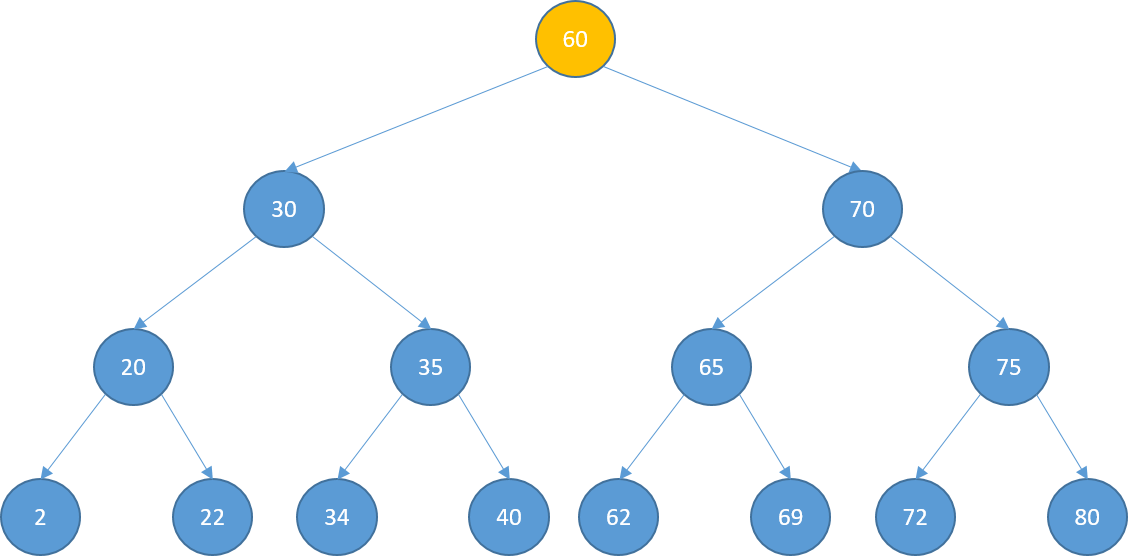
Searching
- Search for 72
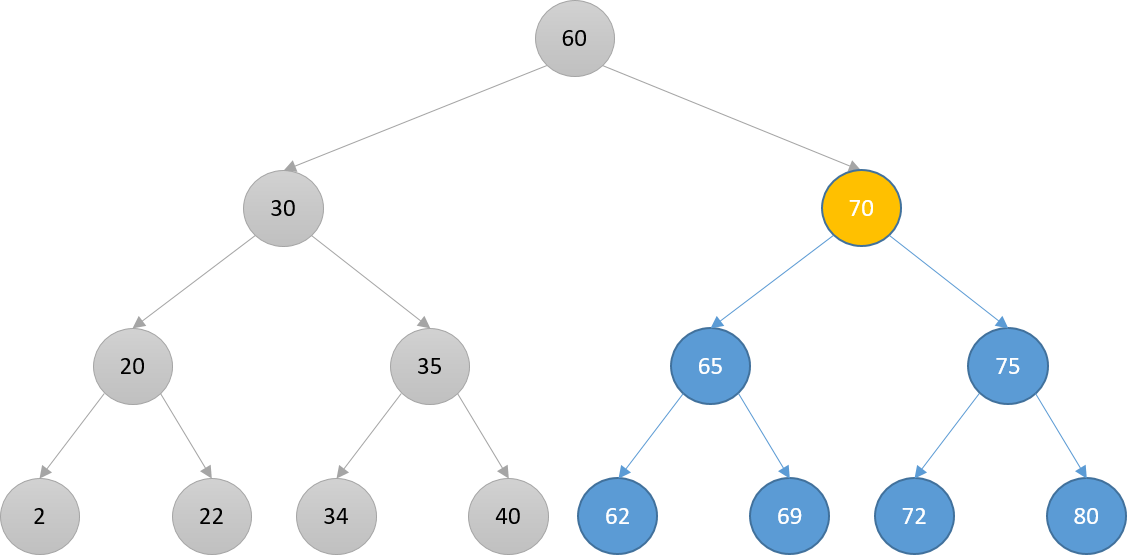
Searching
- Search for 72
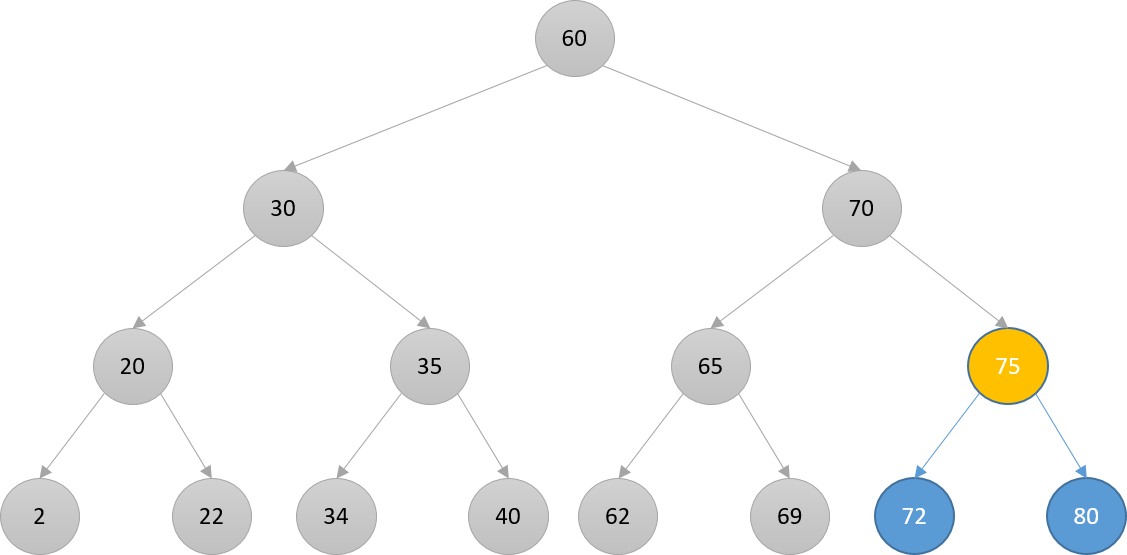
Searching
- Search for 72
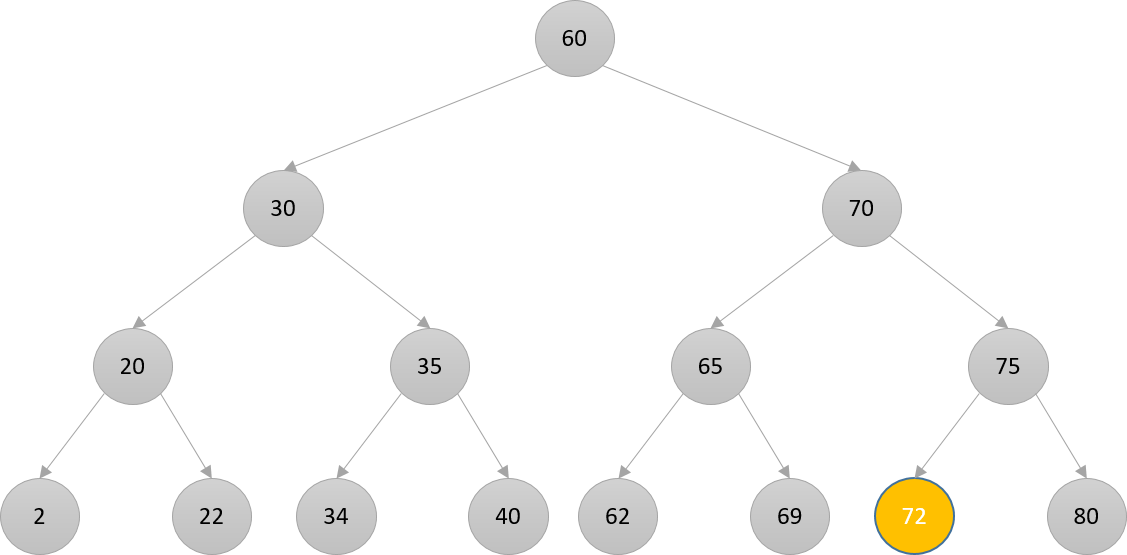
Searching
- Search for 72
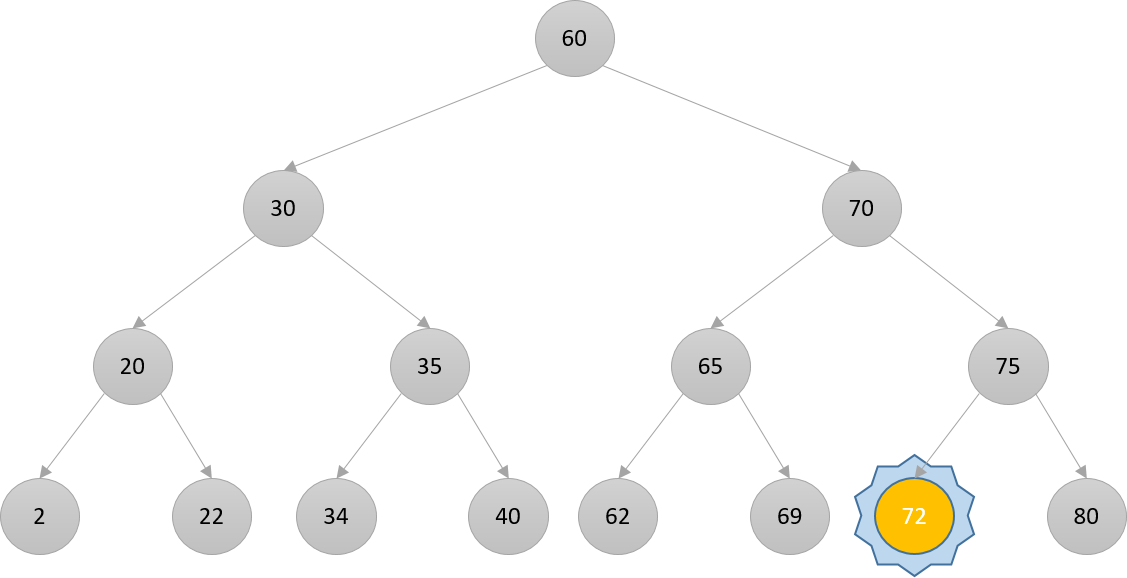
Searching
def search(self, search_value):current_node = self.rootwhile current_node:if search_value == current_node.data:return Trueelif search_value < current_node.data:current_node = current_node.left_childelse:current_node = current_node.right_childreturn False
Inserting
def insert(self, data):new_node = TreeNode(data)if self.root == None:

Inserting
def insert(self, data):
new_node = TreeNode(data)
if self.root == None:
self.root = new_node
return

Inserting
def insert(self, data):
new_node = TreeNode(data)
if self.root == None:
self.root = new_node
return
else:
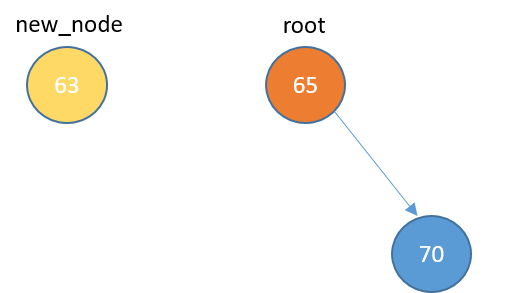
Inserting
def insert(self, data): new_node = TreeNode(data) if self.root == None: self.root = new_node return else: current_node = self.rootwhile True:if data < current_node.data:if current_node.left_child == None:
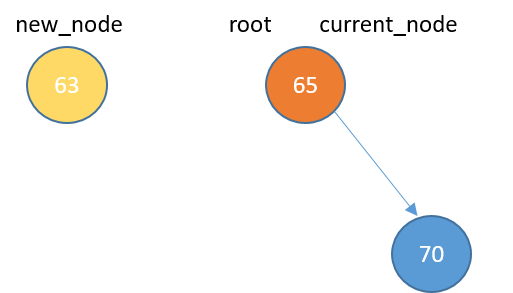
Inserting
def insert(self, data):
new_node = TreeNode(data)
if self.root == None:
self.root = new_node
return
else:
current_node = self.root
while True:
if data < current_node.data:
if current_node.left_child == None:
current_node.left_child = new_node
return
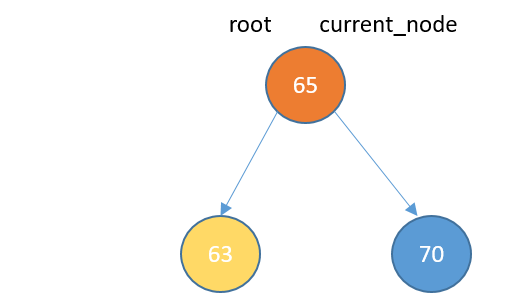
Inserting
def insert(self, data):
new_node = TreeNode(data)
if self.root == None:
self.root = new_node
return
else:
current_node = self.root
while True:
if data < current_node.data:
if current_node.left_child == None:
current_node.left_child = new_node
return
else:
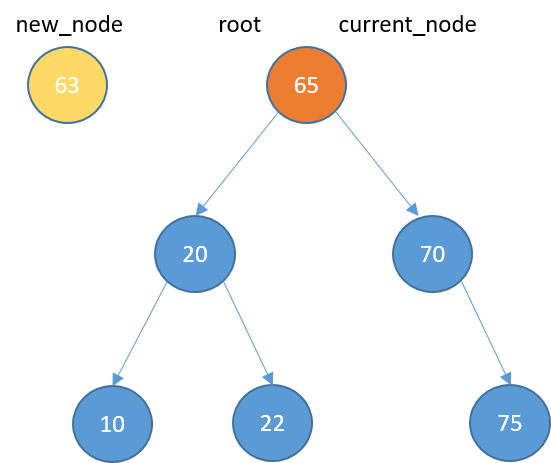
Inserting
def insert(self, data):
new_node = TreeNode(data)
if self.root == None:
self.root = new_node
return
else:
current_node = self.root
while True:
if data < current_node.data:
if current_node.left_child == None:
current_node.left_child = new_node
return
else:
current_node = current_node.left_child
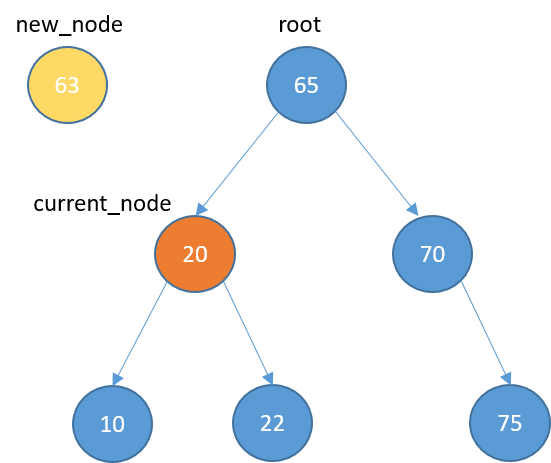
Inserting
def insert(self, data): new_node = TreeNode(data) if self.root == None: self.root = new_node return else: current_node = self.root while True: if data < current_node.data: if current_node.left_child == None: current_node.left_child = new_node return else: current_node = current_node.left_child elif data > current_node.data:if current_node.right_child == None:
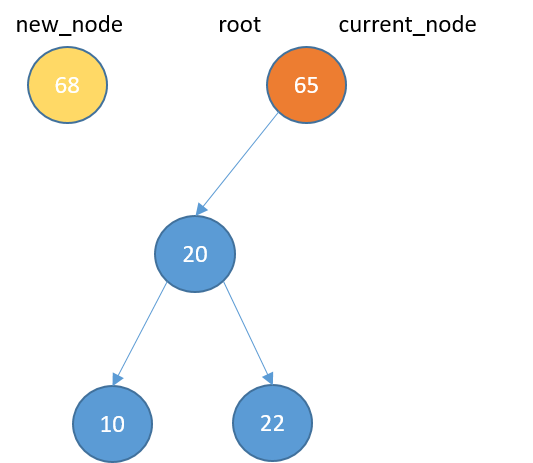
Inserting
def insert(self, data):
new_node = TreeNode(data)
if self.root == None:
self.root = new_node
return
else:
current_node = self.root
while True:
if data < current_node.data:
if current_node.left_child == None:
current_node.left_child = new_node
return
else:
current_node = current_node.left_child
elif data > current_node.data:
if current_node.right_child == None:
current_node.right_child = new_node
return
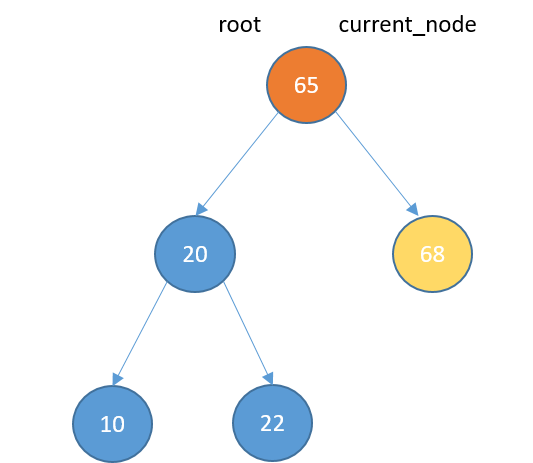
Inserting
def insert(self, data):
new_node = TreeNode(data)
if self.root == None:
self.root = new_node
return
else:
current_node = self.root
while True:
if data < current_node.data:
if current_node.left_child == None:
current_node.left_child = new_node
return
else:
current_node = current_node.left_child
elif data > current_node.data:
if current_node.right_child == None:
current_node.right_child = new_node
return
else:
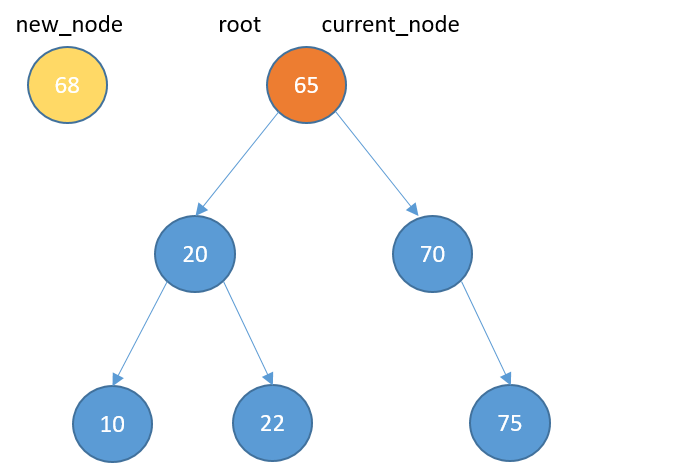
Inserting
def insert(self, data):
new_node = TreeNode(data)
if self.root == None:
self.root = new_node
return
else:
current_node = self.root
while True:
if data < current_node.data:
if current_node.left_child == None:
current_node.left_child = new_node
return
else:
current_node = current_node.left_child
elif data > current_node.data:
if current_node.right_child == None:
current_node.right_child = new_node
return
else:
current_node = current_node.right_child
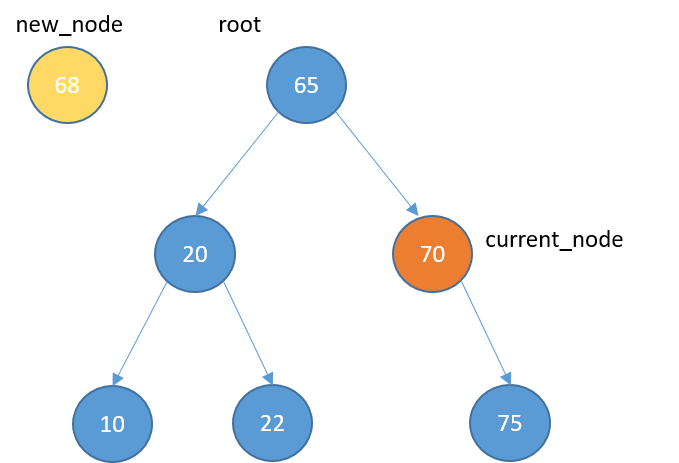
Inserting
def insert(self, data):
new_node = TreeNode(data)
if self.root == None:
self.root = new_node
return
else:
current_node = self.root
while True:
if data < current_node.data:
if current_node.left_child == None:
current_node.left_child = new_node
return
else:
current_node = current_node.left_child
elif data > current_node.data:
if current_node.right_child == None:
current_node.right_child = new_node
return
else:
current_node = current_node.right_child
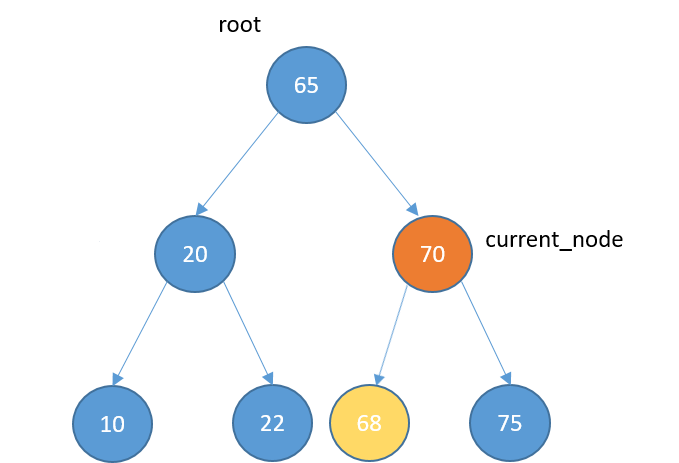
Deleting
- No children
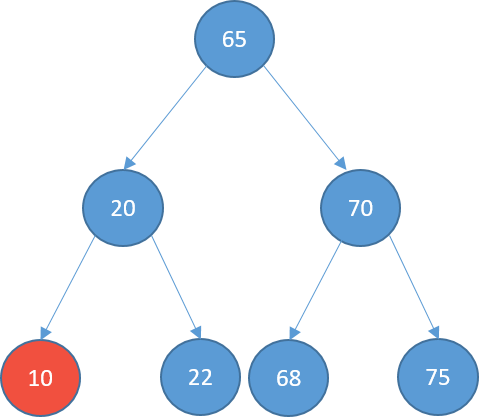
Deleting
- No children
- delete it
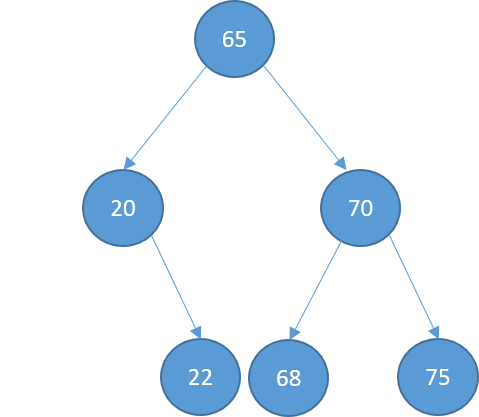
Deleting
- One child
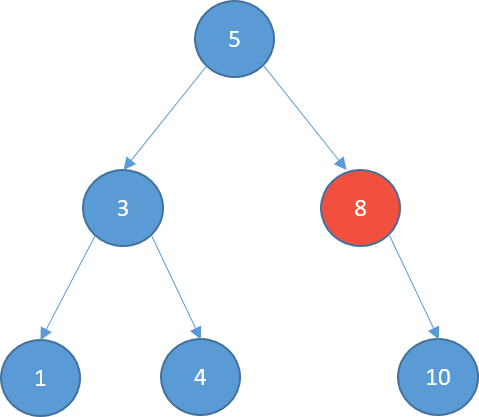
Deleting
- One child
- delete it
- connect the child with node's parent
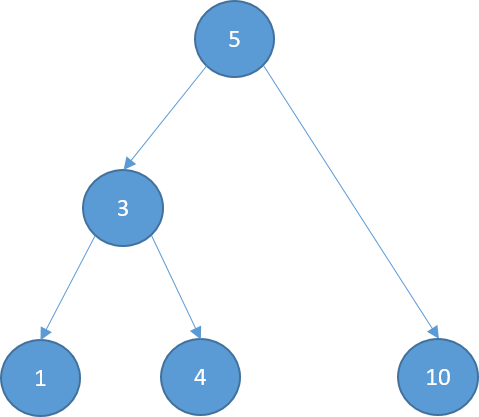
Deleting
- One child
- delete it
- connect the child with node's parent
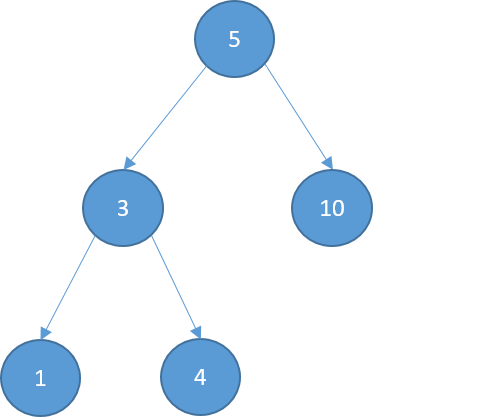
Deleting
- Two children
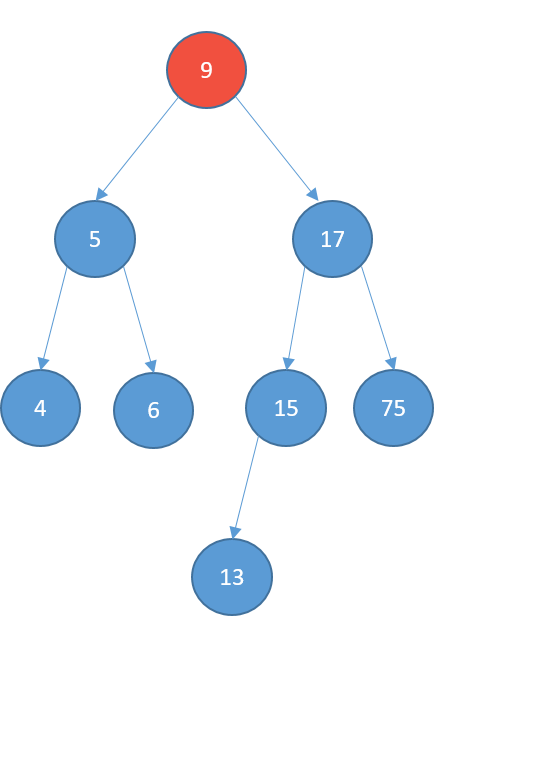
Deleting
- Two children
- replace it with its successor
- the node with the smallest value greater than the value of the node
- find the successor:
- replace it with its successor
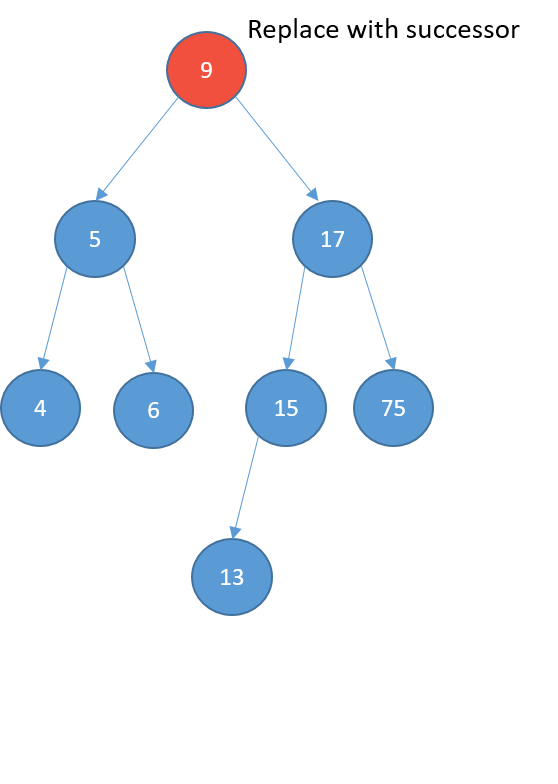
Deleting
- Two children
- replace it with its successor
- the node with the least value greater than the value of the node
- find the successor:
- visit the right child
- replace it with its successor
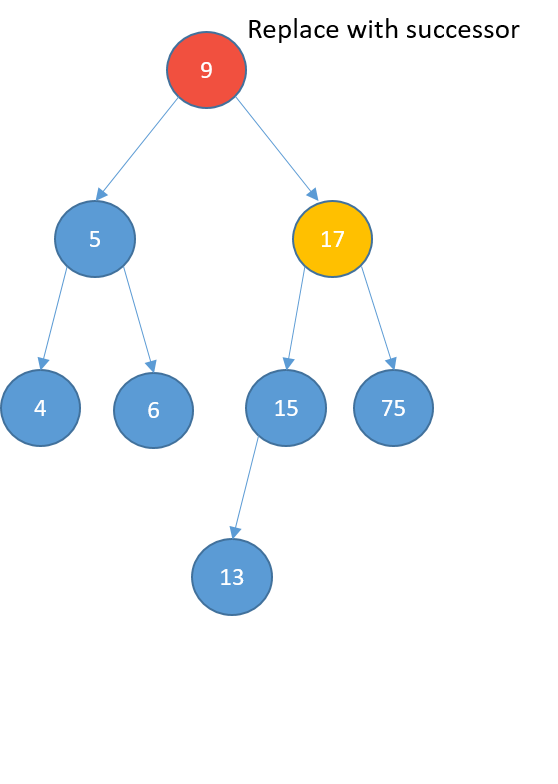
Deleting
- Two children
- replace it with its successor
- the node with the least value greater than the value of the node
- find the successor:
- visit the right child
- keep visiting the left nodes until the end
- replace it with its successor
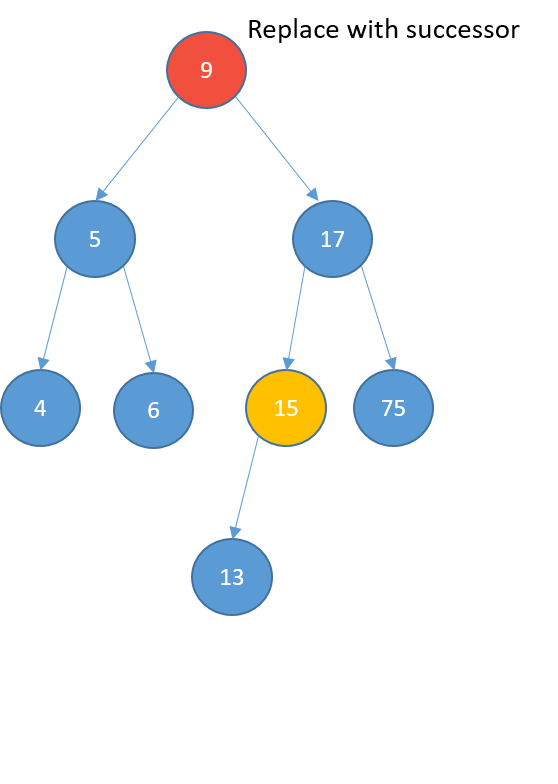
Deleting
- Two children
- replace it with its successor
- the node with the least value greater than the value of the node
- find the successor:
- visit the right child
- keep visiting the left nodes until the end
- replace it with its successor
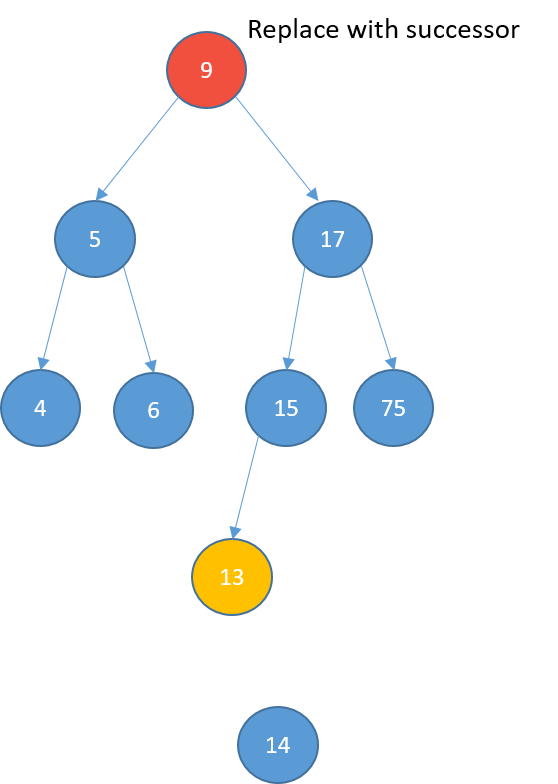
Deleting
- Two children
- replace it with its successor
- the node with the least value greater than the value of the node
- find the successor:
- visit the right child
- keep visiting the left nodes until the end
- replace it with its successor
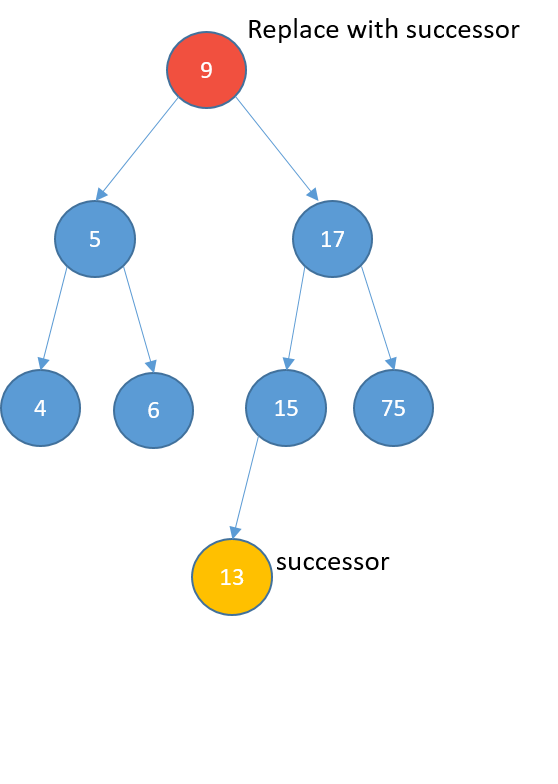
Deleting
- Two children
- replace it with its successor
- the node with the least value greater than the value of the node
- find the successor:
- visit the right child
- keep visiting the left nodes until the end
- replace it with its successor
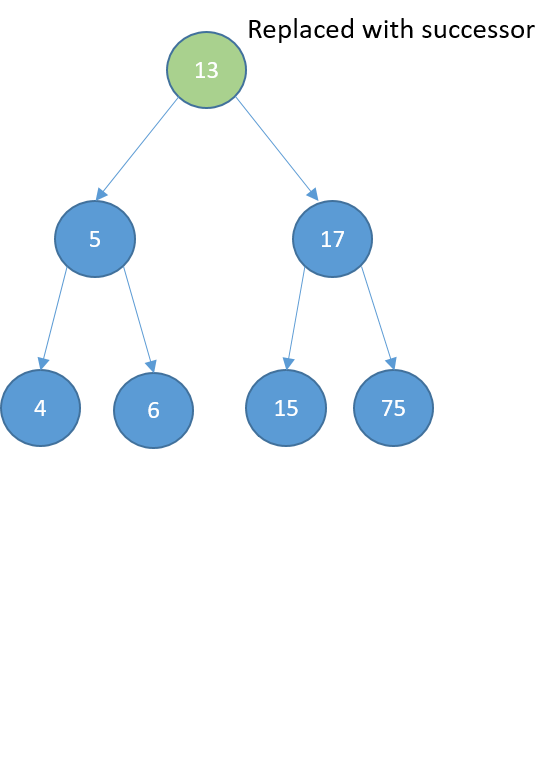
Deleting
- Two children
- replace it with its successor
- the node with the least value greater than the value of the node
- find the successor:
- visit the right child
- keep visiting the left nodes until the end
- if the successor has a right child:
- replace it with its successor
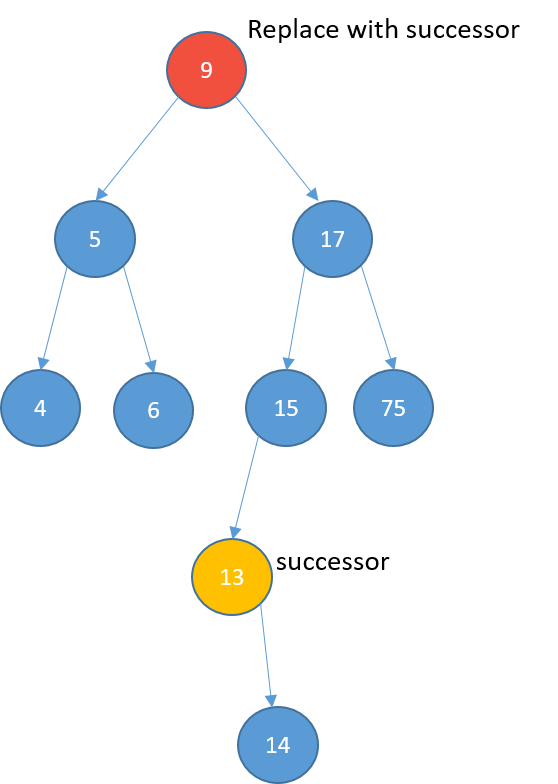
Deleting
- Two children
- replace it with its successor
- the node with the least value greater than the value of the node
- find the successor:
- visit the right child
- keep visiting the left nodes until the end
- if the successor has a right child:
- child becomes the left child of successor's parent.
- replace it with its successor
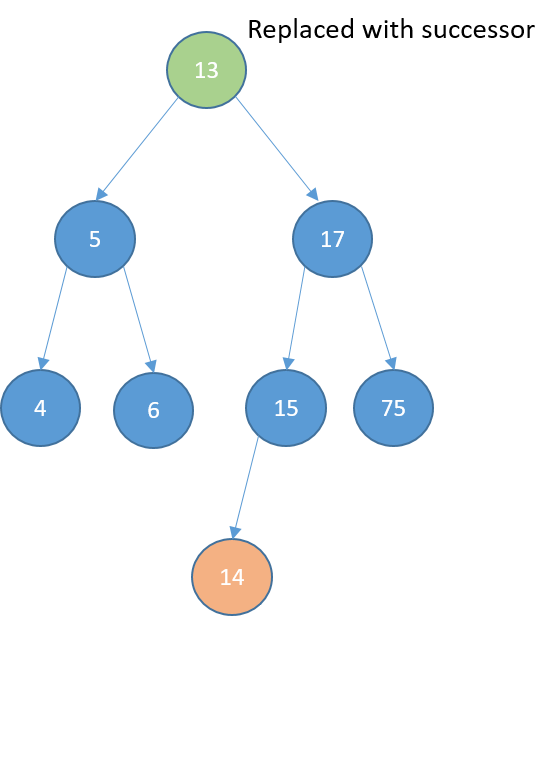
Uses
- Order lists efficiently
- Much faster at searching than arrays and linked lists
- Much faster at inserting and deleting than arrays
- Used to implement more advanced data structures:
- dynamic sets
- lookup tables
- priority queues
Let's practice!
Data Structures and Algorithms in Python

