Les bases de la régression linéaire

Apprentissage supervisé avec scikit-learn

George Boorman

Core Curriculum Manager, DataCamp

Mécanisme de régression

  • $y = ax + b$

    • La régression linéaire simple utilise une caractéristique

      • $y$ = cible

      • $x$ = caractéristique unique

      • $a$, $b$ = paramètres/coefficients du modèle : pente, ordonnée à l’origine

  • Comment choisir $a$ et $b$ ?

    • Définissez une fonction d’erreur pour une ligne donnée

    • Choisissez la ligne qui minimise la fonction d’erreur

  • Fonction d’erreur = fonction de perte = fonction de coût

Apprentissage supervisé avec scikit-learn

La fonction de perte

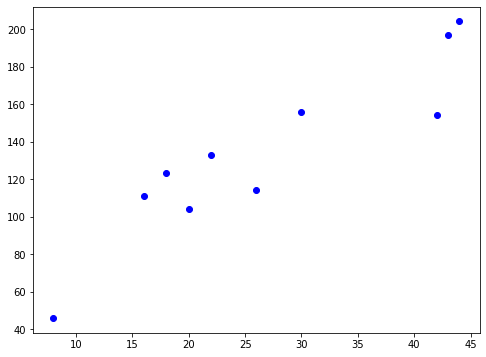
Diagramme en nuage de points

Apprentissage supervisé avec scikit-learn

La fonction de perte

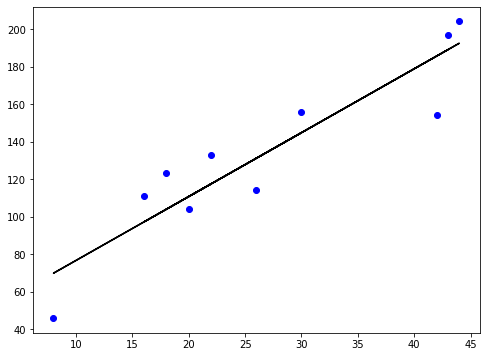
ligne de régression allant du bas à gauche au haut à droite, en passant par le milieu des observations

Apprentissage supervisé avec scikit-learn

La fonction de perte

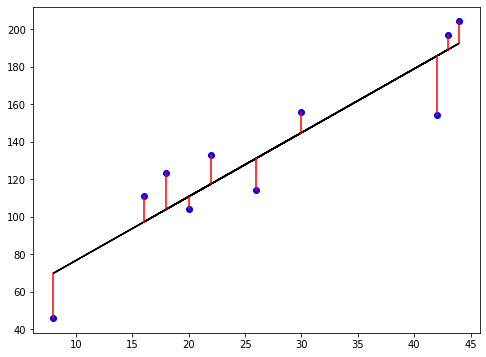
lignes rouges de la ligne de régression à chaque observation

Apprentissage supervisé avec scikit-learn

La fonction de perte

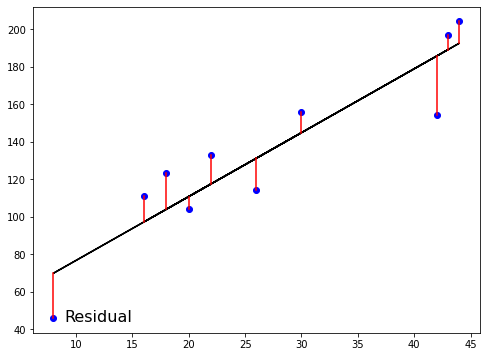
les lignes rouges représentent les résidus

Apprentissage supervisé avec scikit-learn

La fonction de perte

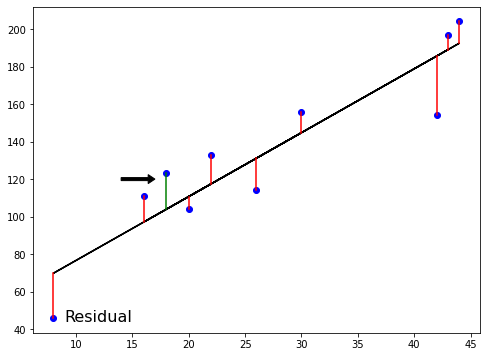
flèche soulignant une flèche positive, car l’observation est au-dessus de la ligne de régression

Apprentissage supervisé avec scikit-learn

Moindres carrés ordinaires

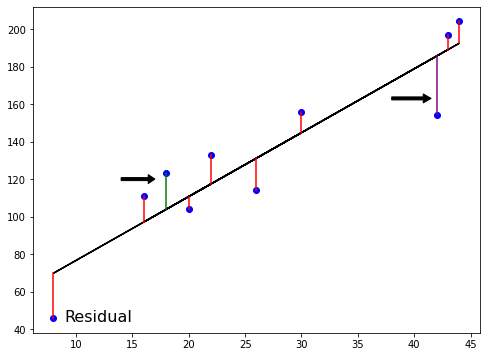
deuxième flèche pointant vers un résidu situé sous la droite de régression, représentant un résidu négatif

$RSS = $ $\displaystyle\sum_{i=1}^{n}(y_i-\hat{y_i})^2$

Moindres carrés ordinaires (MCO) : minimiser RSS

Apprentissage supervisé avec scikit-learn

Régression linéaire dans des dimensions supérieures

$$ y = a_{1}x_{1} + a_{2}x_{2} + b$$

  • Pour ajuster un modèle de régression linéaire ici :
    • Vous devez spécifier 3 variables : $ a_1,\ a_2,\ b $.
  • Dans des dimensions supérieures :
    • Connu sous le nom de régression multiple
    • Vous devez spécifier les coefficients pour chaque caractéristique et la variable $b$

$$ y = a_{1}x_{1} + a_{2}x_{2} + a_{3}x_{3} +... + a_{n}x_{n}+ b$$

  • scikit-learn fonctionne exactement de la même manière :
    • Passez deux tableaux : les caractéristiques et la cible
Apprentissage supervisé avec scikit-learn

Régression linéaire utilisant toutes les caractéristiques

from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.3,
                                                    random_state=42)

reg_all = LinearRegression()

reg_all.fit(X_train, y_train)

y_pred = reg_all.predict(X_test)
Apprentissage supervisé avec scikit-learn

R-carré

  • $R^2$ : quantifie la variance des valeurs cibles expliquée par les caractéristiques

    • Les valeurs sont comprises entre 0 et 1

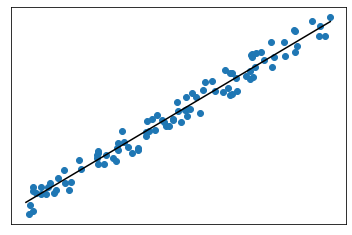
  • $R^2$ élevé :

ligne de régression à 45 degrés allant du bas à gauche au haut à droite et proche de toutes les observations

 

 

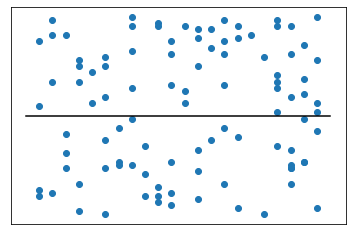
  • $R^2$ faible :

ligne de régression horizontale, où les observations sont dispersées loin de la ligne

Apprentissage supervisé avec scikit-learn

R-carré dans scikit-learn

reg_all.score(X_test, y_test)

0.356302876407827
Apprentissage supervisé avec scikit-learn

Erreur quadratique moyenne (MSE) et racine de l’erreur quadratique moyenne (RMSE)

$MSE = $ $\displaystyle\frac{1}{n}\sum_{i=1}^{n}(y_i-\hat{y_i})^2$

  • Le $MSE$ est mesuré en unités cible, au carré

 

$RMSE = $ $\sqrt{MSE}$

  • Le $RMSE$ se mesure dans les mêmes unités que la variable cible
Apprentissage supervisé avec scikit-learn

RMSE dans scikit-learn

from sklearn.metrics import root_mean_squared_error


root_mean_squared_error(y_test, y_pred)

24.028109426907236
Apprentissage supervisé avec scikit-learn

Passons à la pratique !

Apprentissage supervisé avec scikit-learn

Preparing Video For Download...