Mises en garde sur les corrélations

Introduction aux statistiques en R

Maggie Matsui

Content Developer, DataCamp

Relations non linéaires

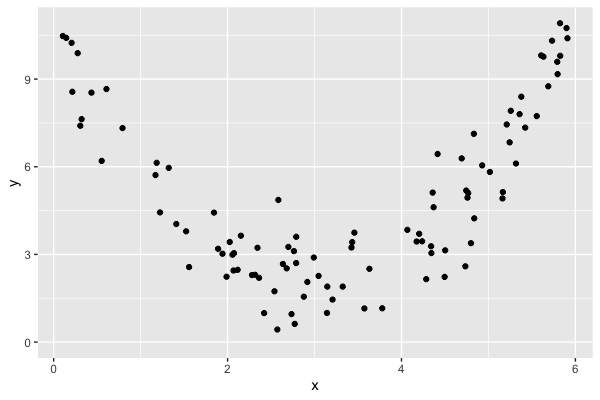
Diagramme en nuages de points des variables ayant une relation quadratique

$$r = 0.18$$

Introduction aux statistiques en R

Relations non linéaires

Ce que nous voyons :

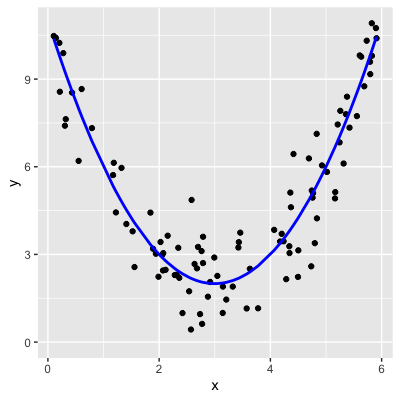
diagramme en nuage de points des variables ayant une relation quadratique avec une ligne de tendance quadratique

Ce que le coefficient de corrélation voit :

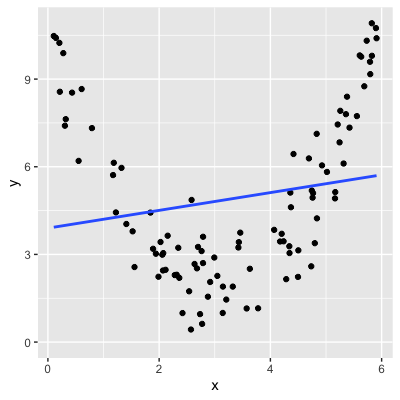
diagramme en nuage de points des variables ayant une relation quadratique avec une ligne de tendance linéaire

Introduction aux statistiques en R

La corrélation ne tient compte que des relations linéaires

La corrélation ne doit pas être utilisée aveuglément

cor(df$x, df$y)

0.1786163

Visualisez toujours vos données

diagramme en nuages de points des variables ayant une relation quadratique

Introduction aux statistiques en R

Données sur le sommeil des mammifères

msleep

   name                       vore  sleep_total awake  bodywt
 1 Cheetah                    carni        12.1  11.9  50    
 2 Owl monkey                 omni         17     7     0.48 
 3 Mountain beaver            herbi        14.4   9.6   1.35 
 4 Greater short-tailed shrew omni         14.9   9.1   0.019
 5 Cow                        herbi         4    20   600    
 6 Three-toed sloth           herbi        14.4   9.6   3.85 
 ...
Introduction aux statistiques en R

Poids corporel en fonction du temps d’éveil

Diagramme en nuages de points du poids corporel en fonction du temps d’éveil

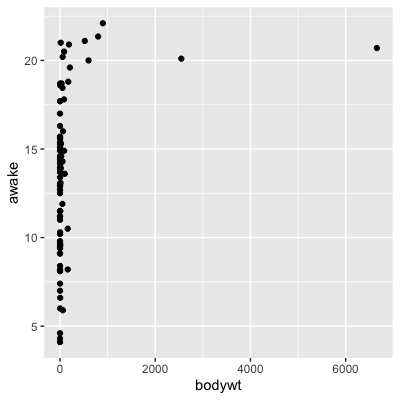
cor(msleep$bodywt, msleep$awake)

0.3119801
Introduction aux statistiques en R

Distribution du poids corporel

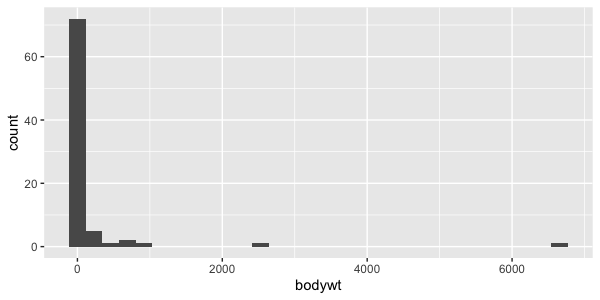
Histogramme de la variable bodywt

Introduction aux statistiques en R

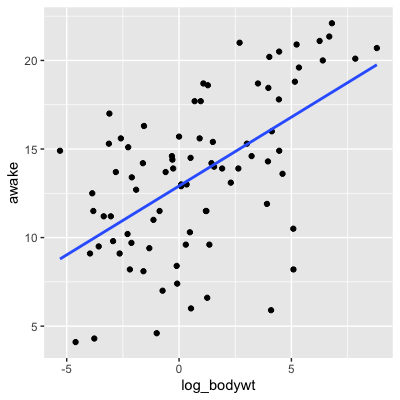
Transformation logarithmique

msleep %>%
  mutate(log_bodywt = log(bodywt)) %>%

  ggplot(aes(log_bodywt, awake)) +
  geom_point() +
  geom_smooth(method = "lm", se = FALSE)

 

cor(msleep$log_bodywt, msleep$awake)

0.5687943

Diagramme en nuages de points du logarithme de bodywt en fonction de l’éveil

Introduction aux statistiques en R

Autres transformations

  • Transformation logarithmique (log(x))
  • Transformation en racine carrée (sqrt(x))

  • Transformation inverse (1 / x)

  • Les combinaisons de ces éléments, par exemple :

    • log(x) et log(y)
    • sqrt(x) et 1 / y
Introduction aux statistiques en R

Pourquoi utiliser une transformation ?

  • Certaines méthodes statistiques s’appuient sur le fait que les variables ont une relation linéaire
    • Coefficient de corrélation
    • Régression linéaire
Introduction aux statistiques en R

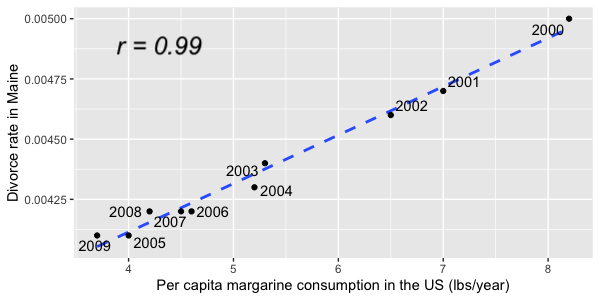
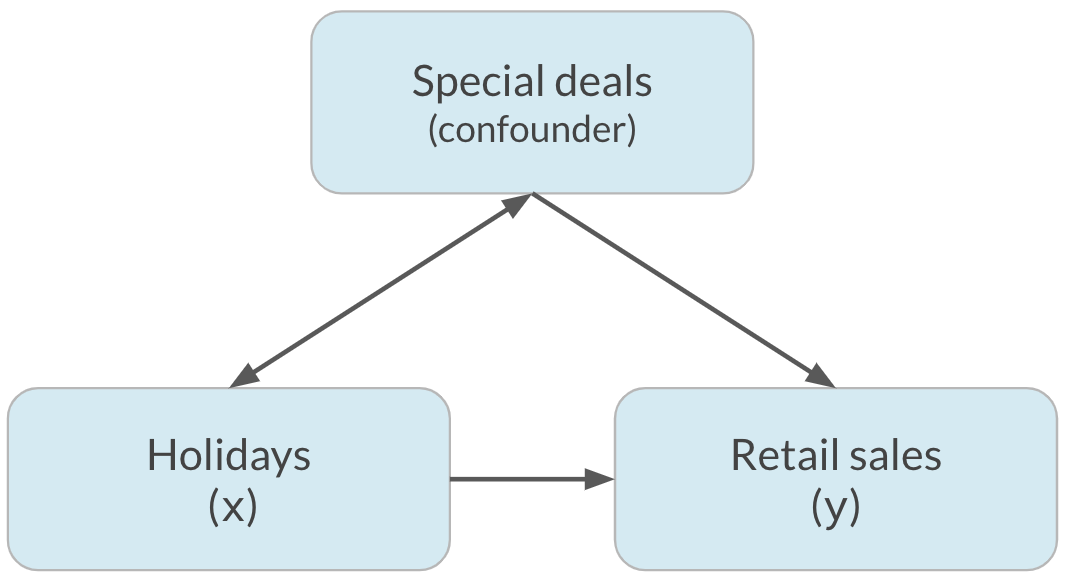
La corrélation n’implique pas la causalité

x est en corrélation avec y ne signifie pas que x entraîne y

Diagramme en nuages de points de la consommation de margarine par habitant aux États-Unis en fonction du taux de divorce dans le Maine. Les variables sont fortement corrélées avec un coefficient de corrélation de 0,99

Introduction aux statistiques en R

Confusion

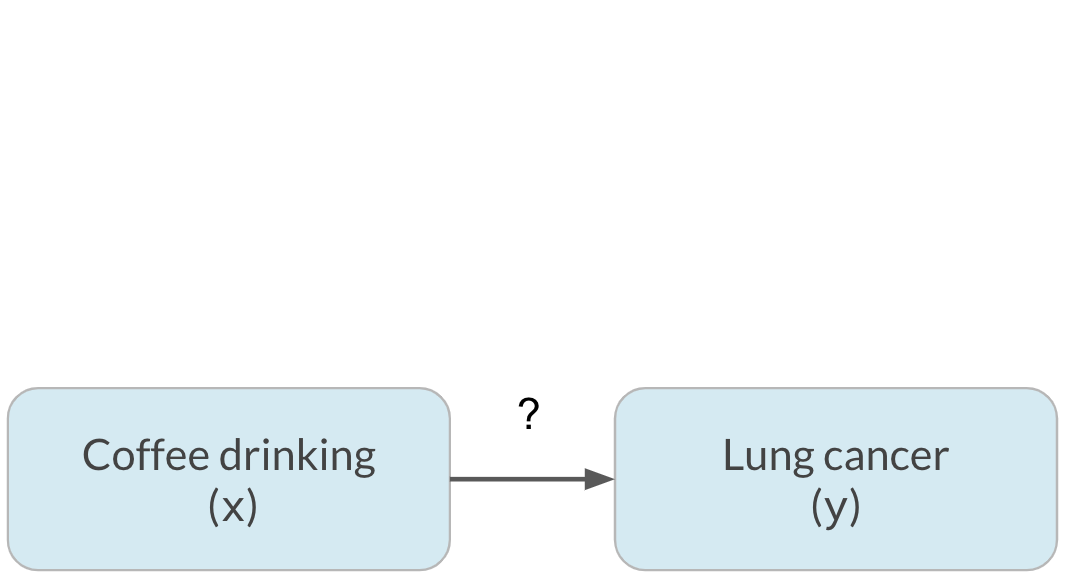
  La consommation de café (x) indique le cancer du poumon (y)

Introduction aux statistiques en R

Confusion

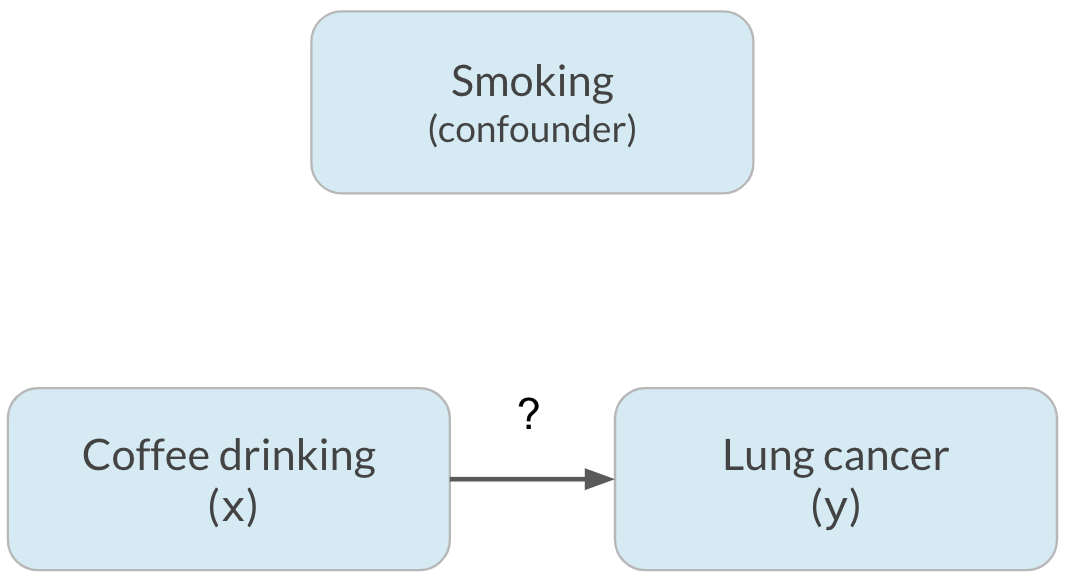
  La consommation de café (x) indique le cancer du poumon (y) avec le tabagisme (facteur de confusion) ci-dessus

Introduction aux statistiques en R

Confusion

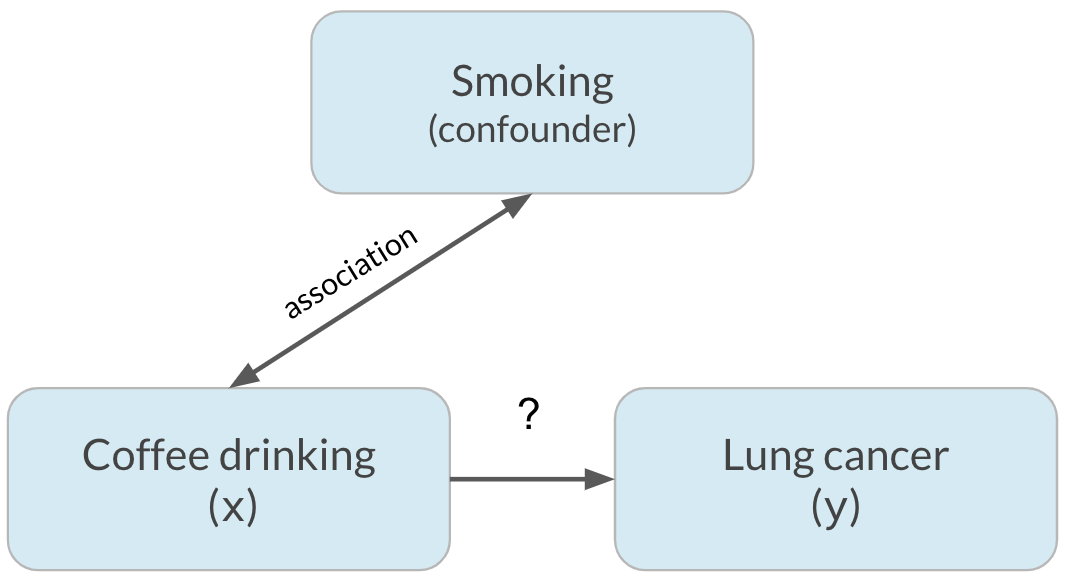
  La consommation de café (x) indique le cancer du poumon (y) avec le tabagisme (facteur de confusion). Double flèche entre le tabagisme et la consommation de café, étiquetée « association ».

Introduction aux statistiques en R

Confusion

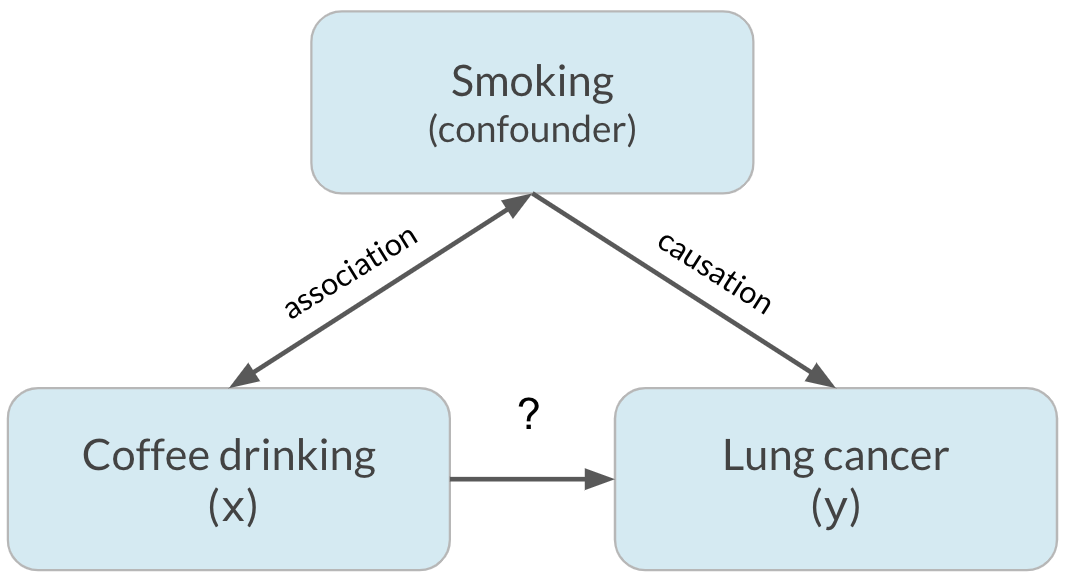
  La consommation de café (x) indique le cancer du poumon (y) avec le tabagisme (facteur de confusion). Double flèche entre le tabagisme et la consommation de café, étiquetée « association ». Flèche entre le tabagisme et le cancer du poumon, étiquetée « causalité »

Introduction aux statistiques en R

Confusion

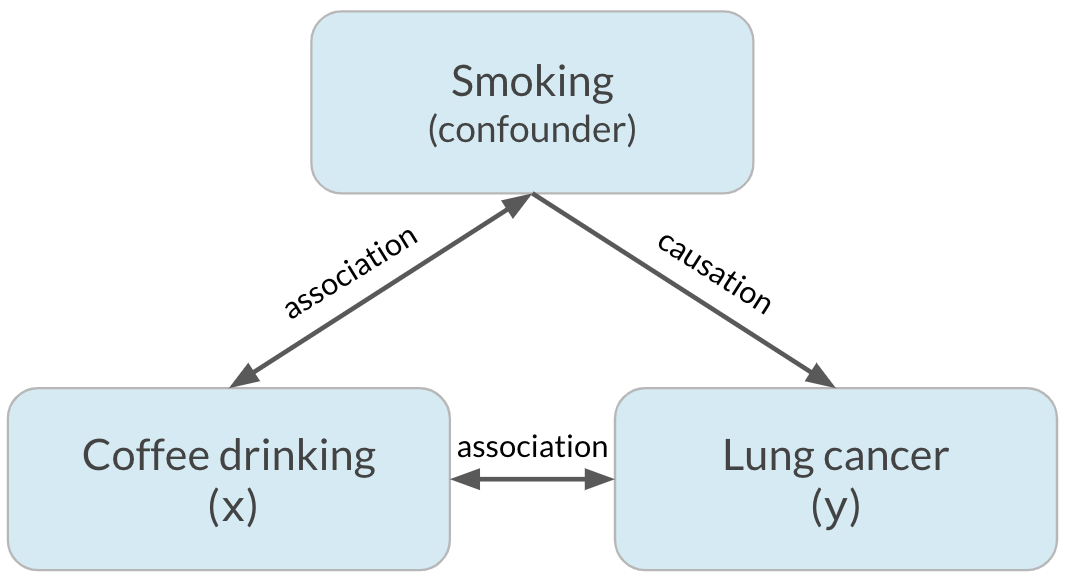
  Consommation de café (x) avec double flèche vers le cancer du poumon (y) étiquetée « association ». Double flèche entre le tabagisme et la consommation de café, étiquetée « association ». Flèche entre le tabagisme et le cancer du poumon, étiquetée « causalité ».

  Les vacances (x) indiquent des ventes au détail (y). Les offres spéciales (facteur de confusion) ont une flèche double vers les vacances et une flèche simple vers les ventes au détail.

Introduction aux statistiques en R

Passons à la pratique !

Introduction aux statistiques en R

Preparing Video For Download...