Corrélation
Introduction aux statistiques en R

Maggie Matsui
Content Developer, DataCamp
Relations entre deux variables
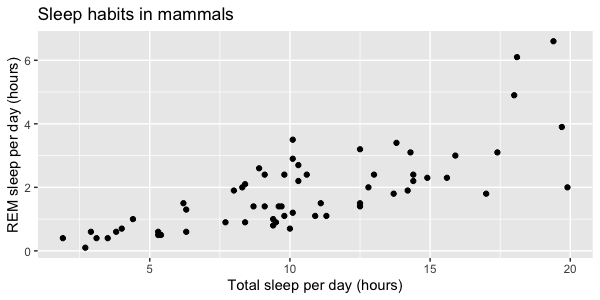
- x = variable explicative/indépendante
- y = variable de réponse/dépendante
Coefficient de corrélation
- Quantifie la relation linéaire entre deux variables
- Nombre compris entre -1 et 1
- La valeur absolue correspond à la force de la relation
- Le signe (+ ou -) correspond au sens de la relation
Valeur absolue = force de la relation
0,99 (relation très forte)
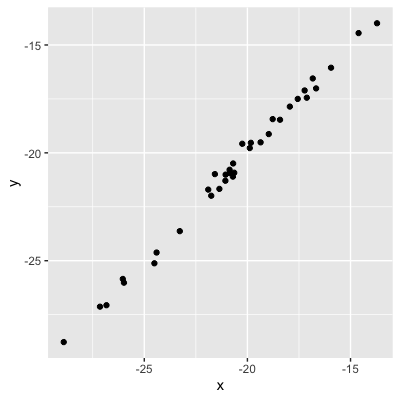
Valeur absolue = force de la relation
0,99 (relation très forte)

0,75 (relation forte)
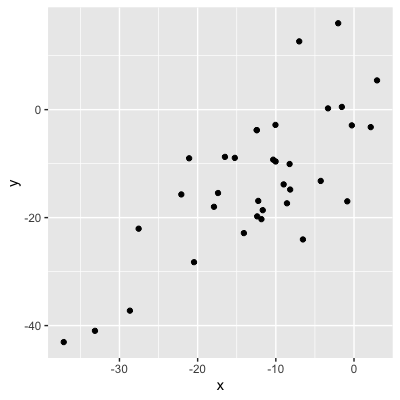
Valeur absolue = force de la relation
0,56 (relation modérée)
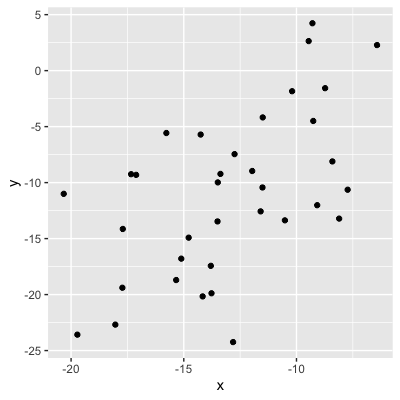
Valeur absolue = force de la relation
0,56 (relation modérée)

0,21 (relation faible)
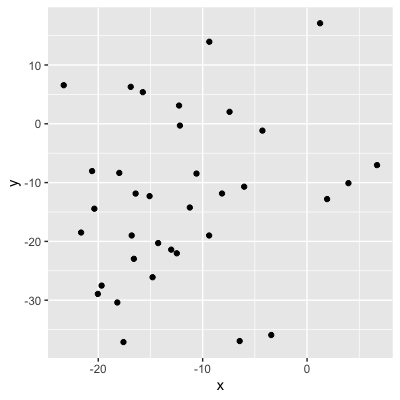
Valeur absolue = force de la relation
0,04 (pas de relation)
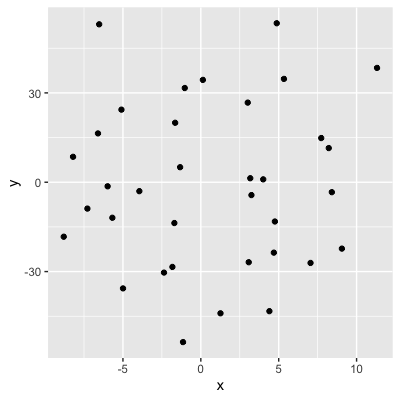
- Connaître la valeur de
xne nous apprend rien sury
Signe = direction
0,75 : lorsque x augmente, y augmente

-0,75 : lorsque x augmente, y diminue
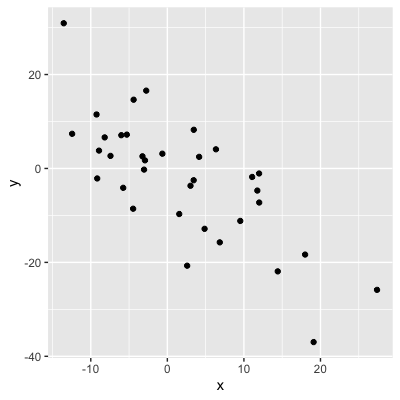
Visualiser les relations
ggplot(df, aes(x, y)) +
geom_point()

Ajout d’une ligne de tendance
ggplot(df, aes(x, y)) + geom_point() +geom_smooth(method = "lm", se = FALSE)
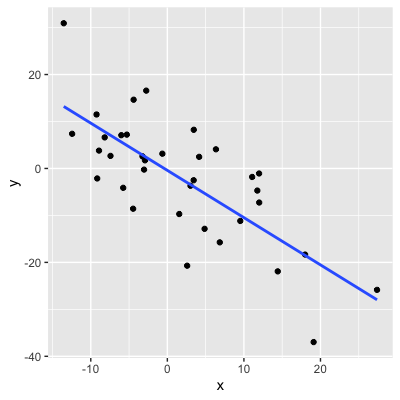
Calcul de la corrélation
cor(df$x, df$y)
-0.7472765
cor(df$y, df$x)
-0.7472765
Corrélation avec les valeurs manquantes
df$x
-3.2508382 -9.1599807 3.4515013 4.1505899 NA 11.9806140 ...
cor(df$x, df$y)
NA
cor(df$x, df$y, use = "pairwise.complete.obs")
-0.7471757
Plusieurs façons de calculer la corrélation
- Formule utilisée dans ce cours : corrélation produit-moment de Pearson ($r$)
- La plus courante
- $\bar{x} =$ moyenne de $x$
$$ r =\frac{\sum ^n _{i=1}(x_i - \bar{x})(y_i - \bar{y})}{\sqrt{\sum ^n _{i=1}(x_i - \bar{x})^2} \sqrt{\sum ^n _{i=1}(y_i - \bar{y})^2}} $$
- Variations de cette formule :
- Tau de Kendall
- Rho de Spearman
Passons à la pratique !
Introduction aux statistiques en R

