Autres distributions de probabilités

Introduction aux statistiques en R

Maggie Matsui

Content Developer, DataCamp

Distribution exponentielle

  • Probabilité de durée entre les événements de Poisson

  • Exemples

    • Probabilité d’un délai de plus d’un jour entre deux adoptions
    • Probabilité d’un délai de moins de 10 minutes entre les arrivées au restaurant
    • Probabilité d’une période de 6 à 8 mois entre les tremblements de terre

  • Utilise également lambda (taux)

  • Continue (temps)

Introduction aux statistiques en R

Demandes de service à la clientèle

  • En moyenne, un ticket de service client est créé toutes les 2 minutes
    • $\lambda$ = 0,5 ticket de service client créé chaque minute

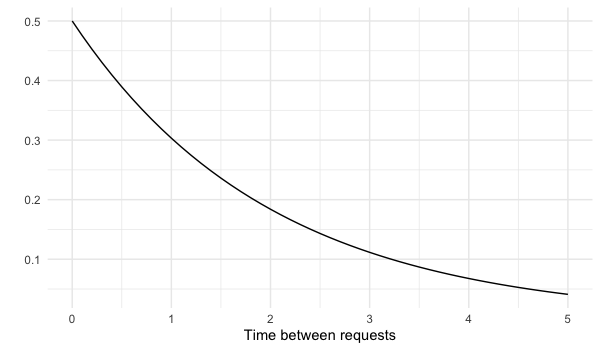
Distribution exponentielle avec lambda = 0,5

Introduction aux statistiques en R

Lambda dans une distribution exponentielle

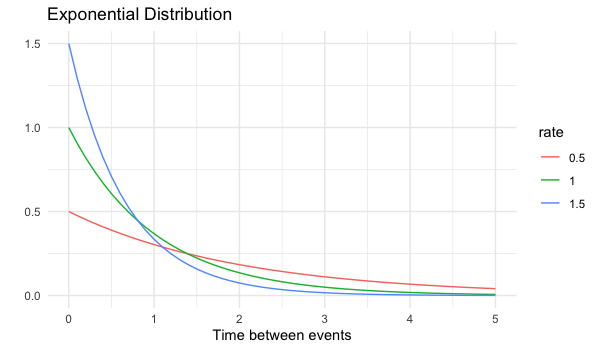
3 distributions exponentielles avec lambda = 0,5, lambda = 1 et lambda = 1,5

Introduction aux statistiques en R

Combien de temps avant la création d’une nouvelle demande ?

$P(\text{wait} < \text{1 min})$ =

pexp(1, rate = 0.5)

0.3934693

$P(\text{wait} > \text{4 min})$ =

pexp(4, rate = 0.5, lower.tail = FALSE)

0.1353353

$P(\text{1 min} < \text{wait} < \text{4 min})$ =

pexp(4, rate = 0.5) - pexp(1, rate = 0.5)

0.4711954
Introduction aux statistiques en R

Valeur attendue d’une distribution exponentielle

En termes de taux (Poisson) :

  • $\lambda$ = $0.5$ requêtes par minute

 

En termes de temps (exponentiel) :

  • $1/\lambda$ = $1$ demande toutes les $2$ minutes
Introduction aux statistiques en R

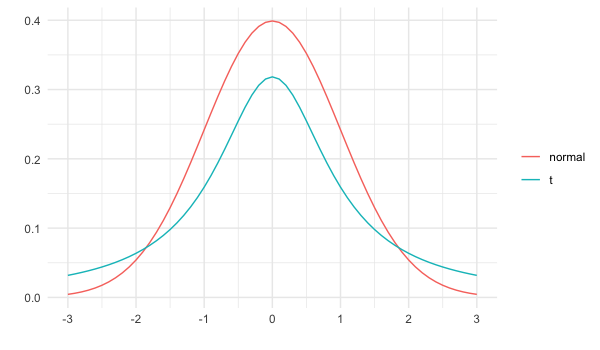
Distribution t (de Student)

  • Forme similaire à la distribution normale

Distribution t et distribution normale tracées sur les mêmes axes

Introduction aux statistiques en R

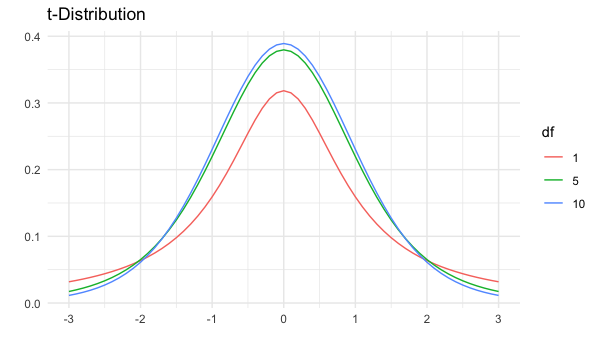
Degrés de liberté

  • Possède un degré de liberté (dl) qui affecte l’épaisseur des queues
    • dl plus faible = queues plus épaisses, écart-type plus élevé
    • dl plus élevé = plus proche de la distribution normale

3 distributions t avec dl = 1, dl = 5, et dl = 10

Introduction aux statistiques en R

Distribution log-normale

  • Variable dont le logarithme est normalement distribué

  • Exemples :

    • Durée de parties d’échecs
    • Pression artérielle chez l’adulte
    • Nombre d’hospitalisations lors de l’épidémie de SRAS en 2003

3 distributions log-normales avec écart-type = 0,5, écart-type = 1, et écart-type = 1,5

Introduction aux statistiques en R

Passons à la pratique !

Introduction aux statistiques en R

Preparing Video For Download...