Mesures de dispersion

Introduction aux statistiques en R

Maggie Matsui

Content Developer, DataCamp

Qu’est-ce que la dispersion ?

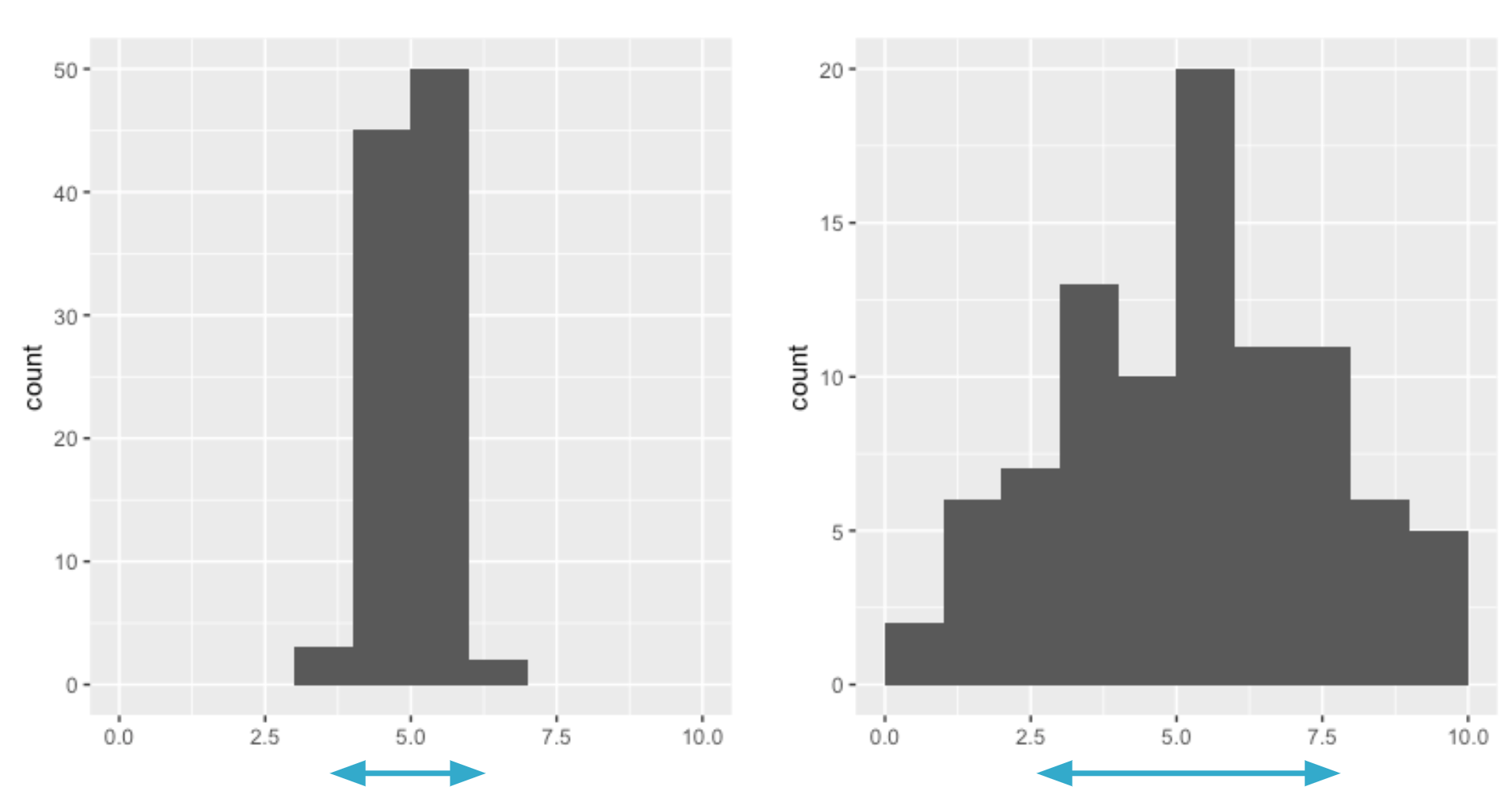
Deux histogrammes : l'un étroit avec des données ne couvrant que quelques valeurs, l’autre plus large avec des données couvrant davantage de valeurs.

Introduction aux statistiques en R

Variance

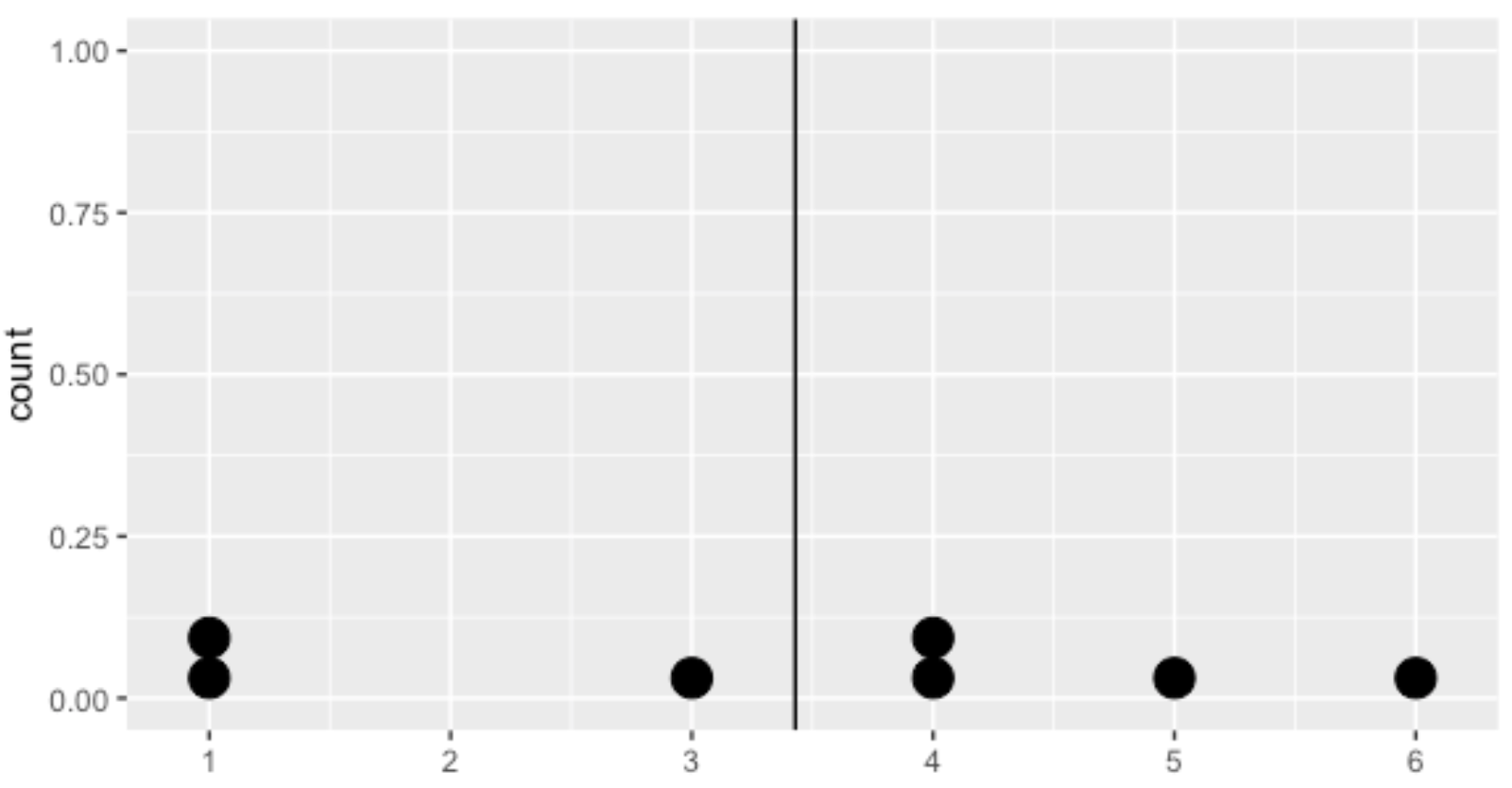
Distance moyenne entre chaque point de données et la moyenne des données Un graphique à points représentant 7 points de données avec une ligne noire au milieu représentant la moyenne.

Introduction aux statistiques en R

Calculer la variance

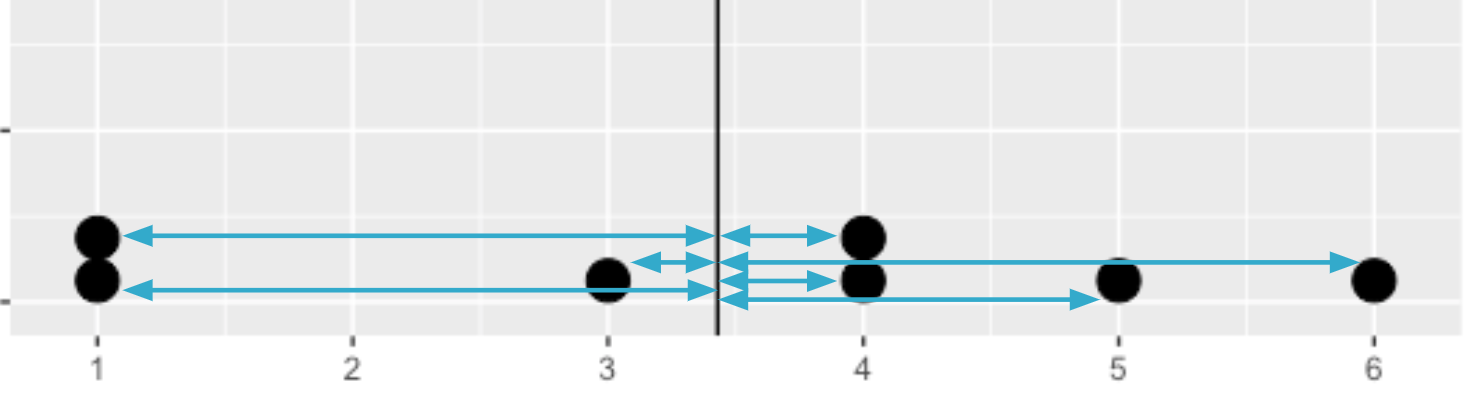
Un graphique à points représentant 7 points de données avec une ligne noire au milieu représentant la moyenne. Des flèches sont tracées entre chaque point et la ligne médiane.

dists <- msleep$sleep_total - mean(msleep$sleep_total)
dists

1.66626506  6.56626506 ... -4.13373494  2.06626506 -0.63373494
Introduction aux statistiques en R

Calculer la variance

squared_dists <- (dists)^2

2.776439251 43.115836841 ... 17.087764552  4.269451299  0.401619974

sum_sq_dists <- sum(squared_dists)
sum_sq_dists

1624.066
Introduction aux statistiques en R

Calculer la variance

sum_sq_dists/82

19.80568

var(msleep$sleep_total)

19.80568
Introduction aux statistiques en R

Écart-type

sqrt(var(msleep$sleep_total))

4.450357

# Standard deviation of 'sleep_total'
sd(msleep$sleep_total)

4.450357
Introduction aux statistiques en R

Écart moyen absolu

dists <- msleep$sleep_total - mean(msleep$sleep_total)
mean(abs(dists))

3.566701

 

Écart-type et écart moyen absolu

  • L’écart-type met les distances au carré, pénalisant davantage les longues distances que les courtes.
  • L’écart moyen absolu pénalise chaque distance de manière égale.
  • L’un n’est pas meilleur que l’autre, mais l’écart-type est plus courant que l’écart moyen absolu.
Introduction aux statistiques en R

Quartiles

quantile(msleep$sleep_total)

   0%   25%   50%   75%  100% 
 1.90  7.85 10.10 13.75 19.90

Deuxième quartile/50e centile = médiane

Introduction aux statistiques en R

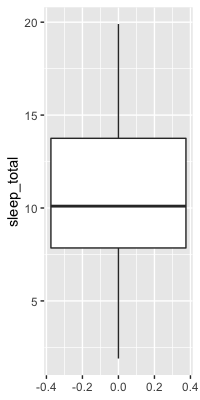
Les diagrammes en boîte utilisent les quartiles

ggplot(msleep, aes(y = sleep_total)) +
  geom_boxplot()

Diagramme en boîte représentant le temps de sommeil total des mammifères

Introduction aux statistiques en R

Quantiles

quantile(msleep$sleep_total, probs = c(0, 0.2, 0.4, 0.6, 0.8, 1))

   0%   20%   40%   60%   80%  100% 
 1.90  6.24  9.48 11.14 14.40 19.90

seq(from, to, by)

quantile(msleep$sleep_total, probs = seq(0, 1, 0.2))

   0%   20%   40%   60%   80%  100% 
 1.90  6.24  9.48 11.14 14.40 19.90
Introduction aux statistiques en R

Écart interquartile (IQR)

Hauteur de la boîte dans un diagramme en boîte

iqr = quantile(msleep$sleep_total, 0.75) - quantile(msleep$sleep_total, 0.25)
iqr

75%
5.9
Introduction aux statistiques en R

Valeurs aberrantes

Valeur aberrante : point de données très différent des autres

Comment savoir ce qu’est une différence substantielle ? Un point de données est une valeur aberrante si :

  • $\text{data} < \text{Q1} - 1.5\times\text{IQR}$ ou
  • \text
Introduction aux statistiques en R

Trouver les valeurs aberrantes

iqr <- quantile(msleep$bodywt, 0.75) - quantile(msleep$bodywt, 0.25)

lower_threshold <- quantile(msleep$bodywt, 0.25) - 1.5 * iqr
upper_threshold<- quantile(msleep$bodywt, 0.75) + 1.5 * iqr

msleep %>% filter(bodywt < lower_threshold | bodywt > upper_threshold ) %>% 
  select(name, vore, sleep_total, bodywt)

# A tibble: 11 x 4
   name                 vore  sleep_total bodywt
   <chr>                <chr>       <dbl>  <dbl> 
 1 Cow                  herbi         4      600 
 2 Asian elephant       herbi         3.9   2547 
 3 Horse                herbi         2.9    521 
 ...
Introduction aux statistiques en R

Passons à la pratique !

Introduction aux statistiques en R

Preparing Video For Download...