La distribution normale

Introduction aux statistiques en R

Maggie Matsui

Content Developer, DataCamp

Qu’est-ce qu’une distribution normale ?

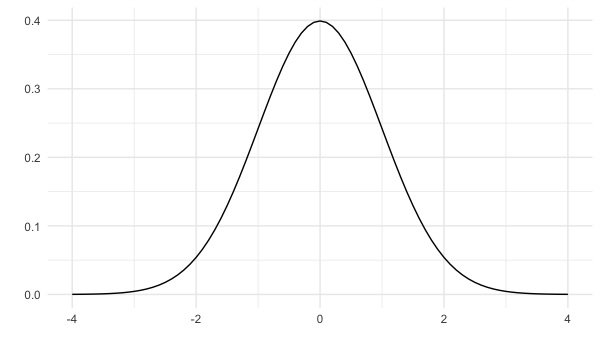
Fonction de densité de la distribution normale

Introduction aux statistiques en R

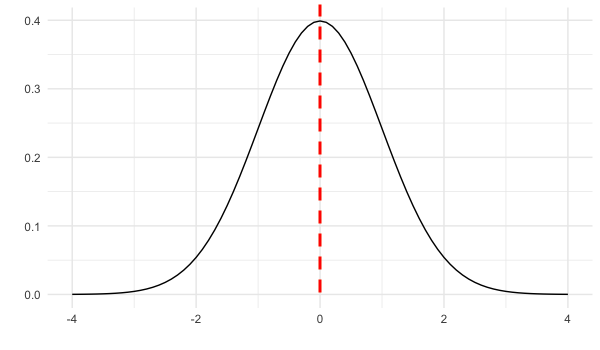
Symétrique

Ligne verticale en pointillé au milieu de la distribution normale

Introduction aux statistiques en R

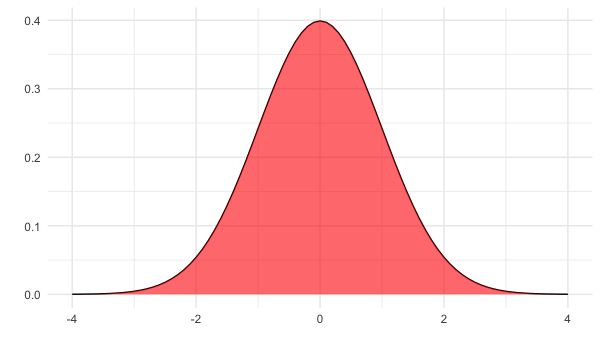
Aire = 1

Distribution normale avec zone sous la courbe ombrée

Introduction aux statistiques en R

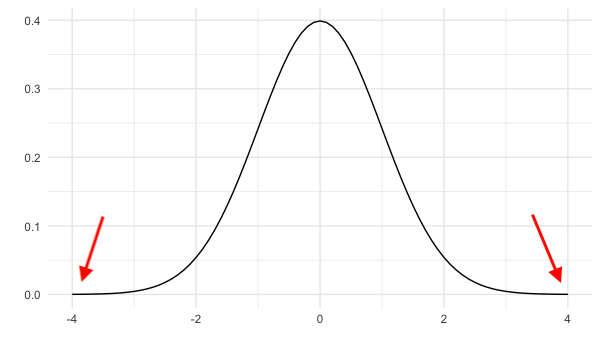
La courbe n’atteint jamais 0

Distribution normale avec des flèches pointant vers les queues de chaque côté

Introduction aux statistiques en R

Décrite par la moyenne et l’écart-type

 

                                                          Moyenne : 20

                                      Écart-type : 3

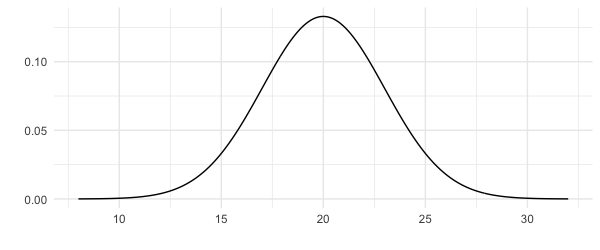
Distribution normale avec une moyenne de 20 et un écart-type de 3

                         Distribution normale standard

                                                           Moyenne : 0

                                      Écart-type : 1

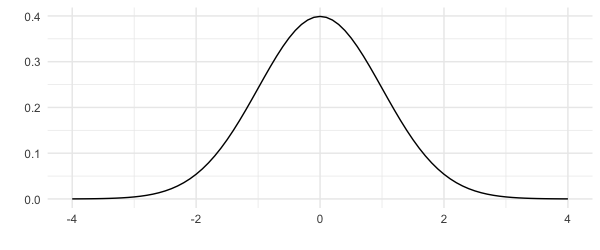
Distribution normale avec une moyenne de 0 et un écart-type de 1

Introduction aux statistiques en R

Décrite par la moyenne et l’écart-type

 

                                                          Moyenne : 20

                                      Écart-type : 3

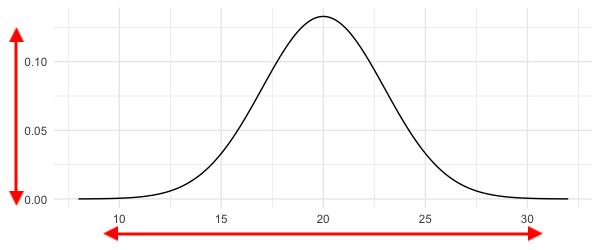
Distribution normale avec une moyenne de 20 et un écart-type de 3

                         Distribution normale standard

                                                           Moyenne : 0

                                      Écart-type : 1

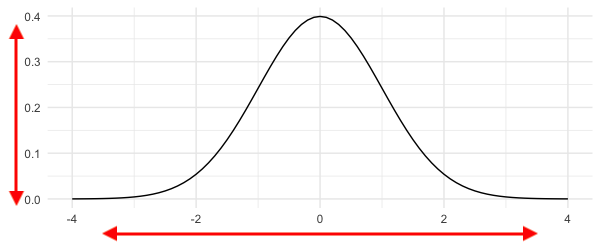
Distribution normale avec une moyenne de 0 et un écart-type de 1

Introduction aux statistiques en R

Zones sous la distribution normale

68 % se situent à au plus un écart-type de la moyenne

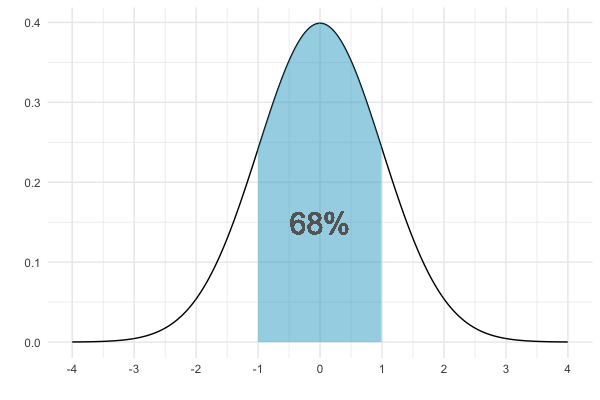
Distribution normale avec zone entre -1 et 1 mise en évidence, étiquetée avec 68 %

Introduction aux statistiques en R

Zones sous la distribution normale

95 % se situent à au plus 2 écarts-types de la moyenne

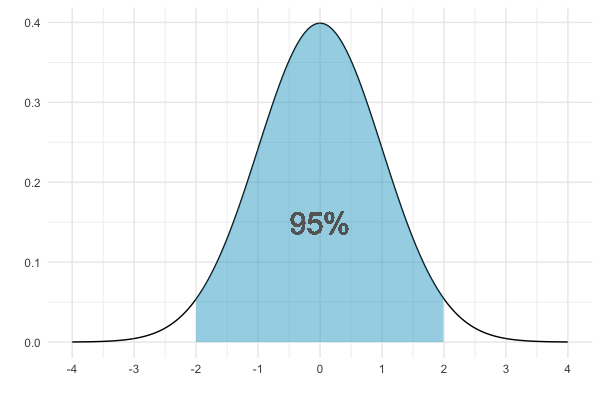
Distribution normale avec zone entre -2 et 2 mise en évidence, étiquetée avec 95 %

Introduction aux statistiques en R

Zones sous la distribution normale

99,7 % se situent à au plus 3 écarts-types de la moyenne

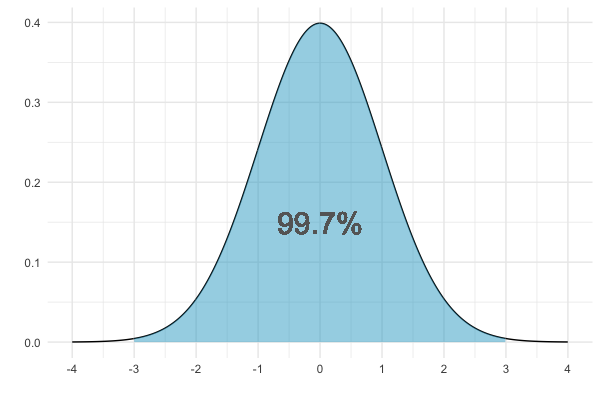
Distribution normale avec la zone entre -3 et 3 mise en évidence, étiquetée avec 99,7 %

Introduction aux statistiques en R

De nombreux histogrammes semblent normaux

Distribution normale

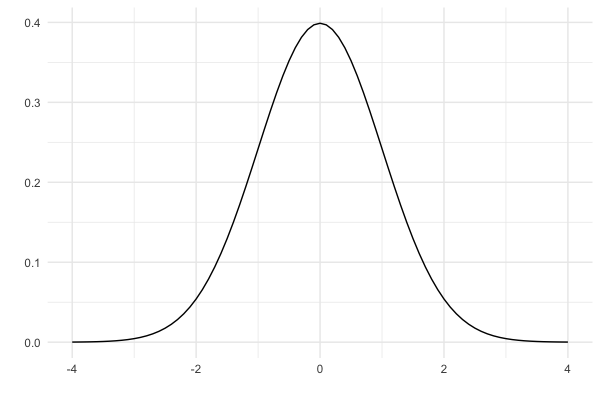
Distribution normale standard

Tailles des femmes (étude NHANES)

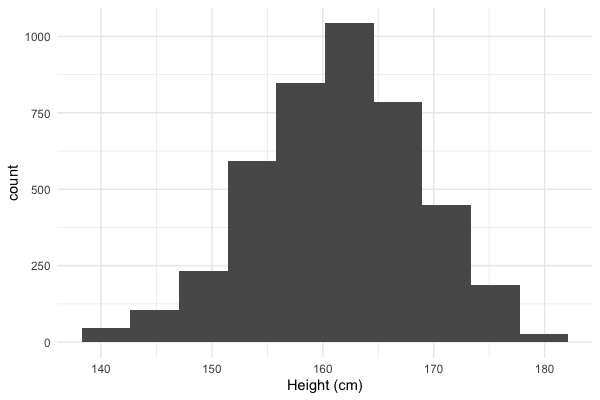
Histogramme des tailles des femmes

  Moyenne : 161 cm      Écart-type : 7 cm

Introduction aux statistiques en R

Approximation des données par une distribution normale

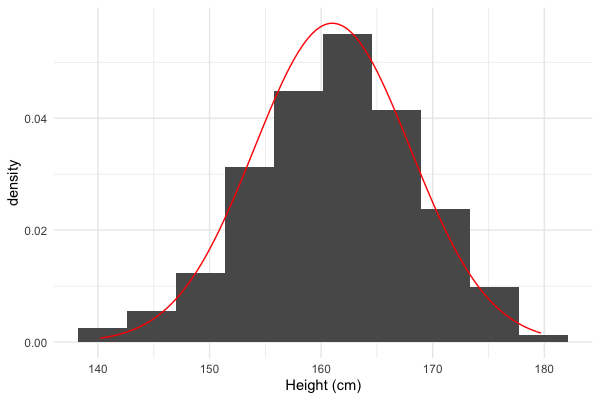
Courbe normale tracée sur l’histogramme des tailles des femmes

Introduction aux statistiques en R

Quel pourcentage de femmes mesurent moins de 154 cm ?

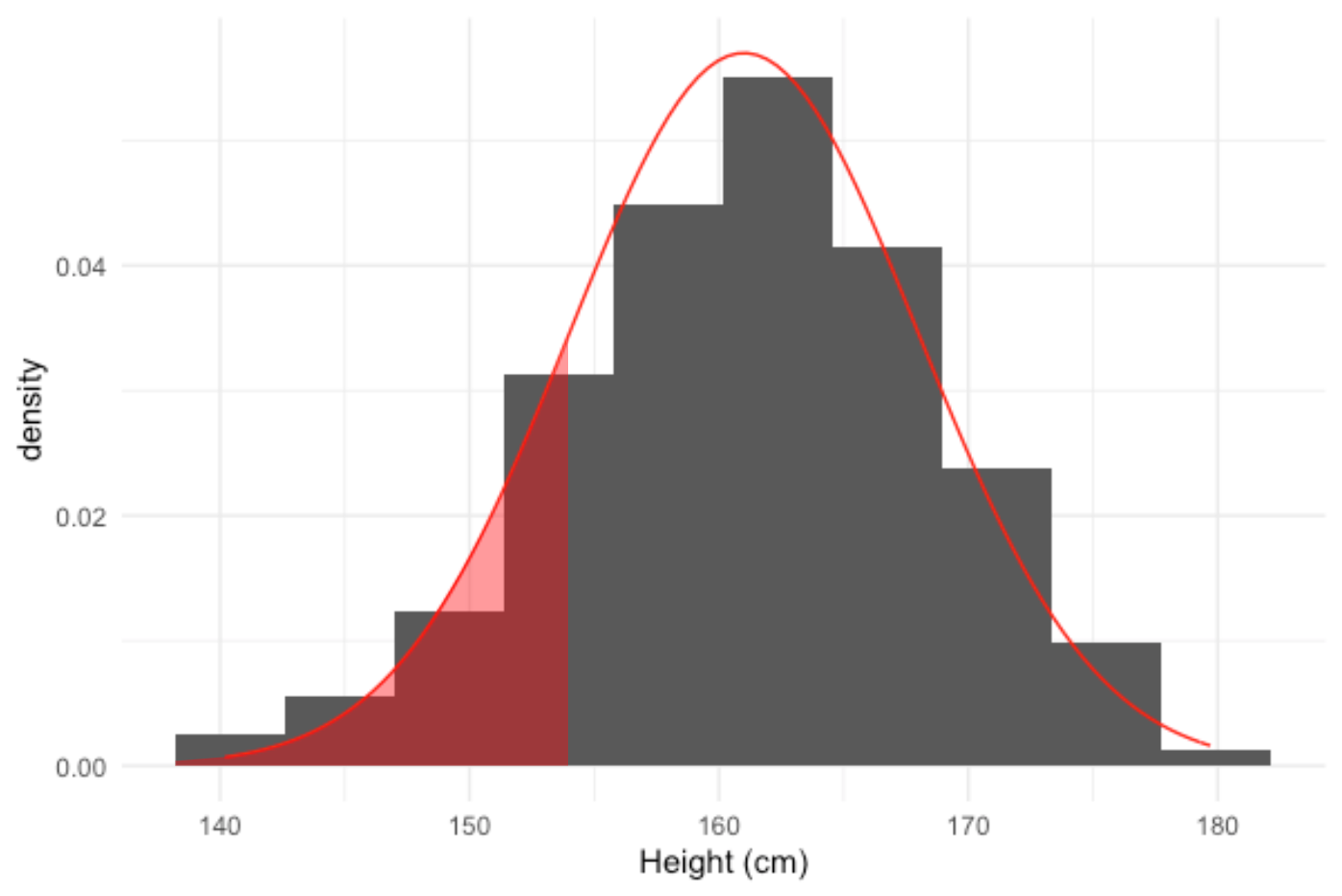
Courbe normale tracée sur l’histogramme des tailles des femmes, la zone inférieure à 154 étant ombrée

16 % des femmes interrogées mesurent moins de 154 cm

pnorm(154, mean = 161, sd = 7)

0.159
Introduction aux statistiques en R

Quel pourcentage de femmes mesurent plus de 154 cm ?

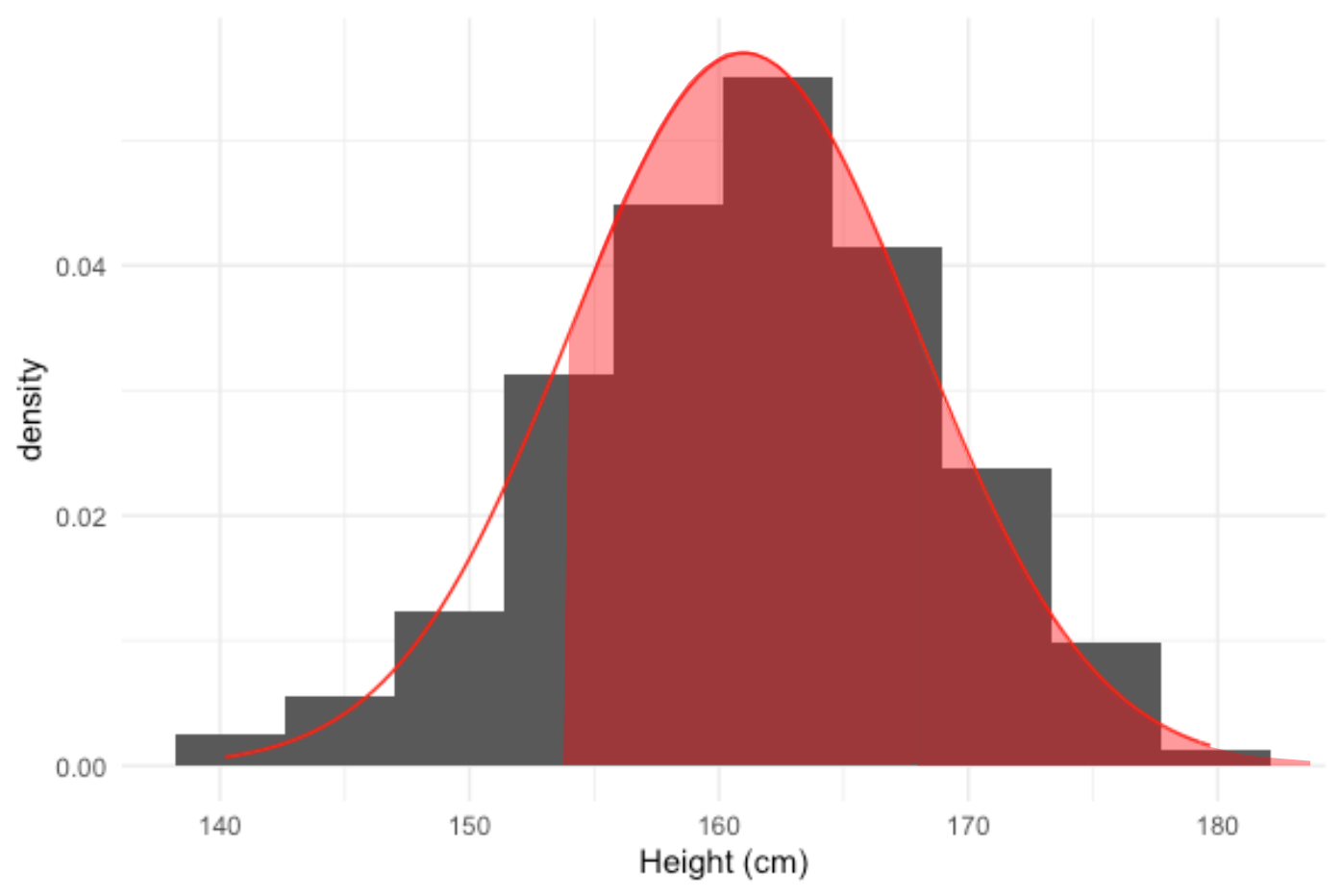
Courbe normale tracée sur l’histogramme des tailles des femmes, la zone à droite de 154 étant ombrée

pnorm(154, mean = 161, sd = 7, 
      lower.tail = FALSE)

0.8413447
Introduction aux statistiques en R

Quel pourcentage de femmes mesurent entre 154 et 157 cm ?

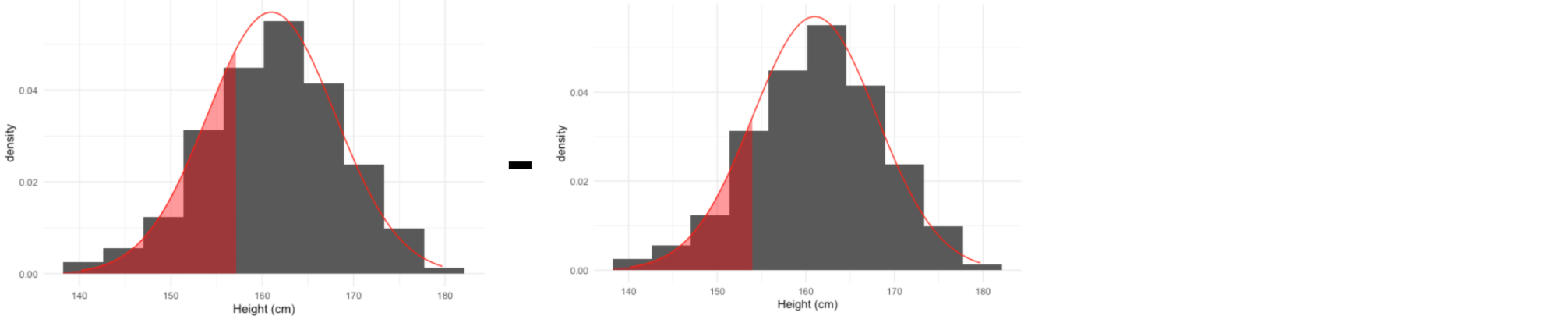
Zone inférieure à 157 moins zone inférieure à 154

pnorm(157, mean = 161, sd = 7) - pnorm(154, mean = 161, sd = 7)
Introduction aux statistiques en R

Quel pourcentage de femmes mesurent entre 154 et 157 cm ?

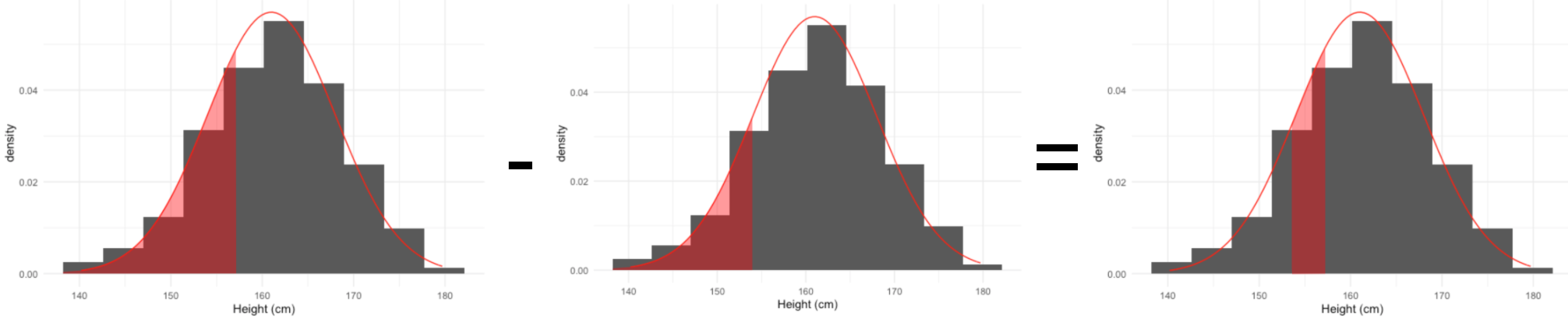
L’aire de la zone inférieure à 157 moins l’aire de la zone inférieure à 154 est égale à l’aire de la zone comprise entre 154 et 157

pnorm(157, mean = 161, sd = 7) - pnorm(154, mean = 161, sd = 7)

0.1252
Introduction aux statistiques en R

90 % des femmes mesurent moins de combien ?

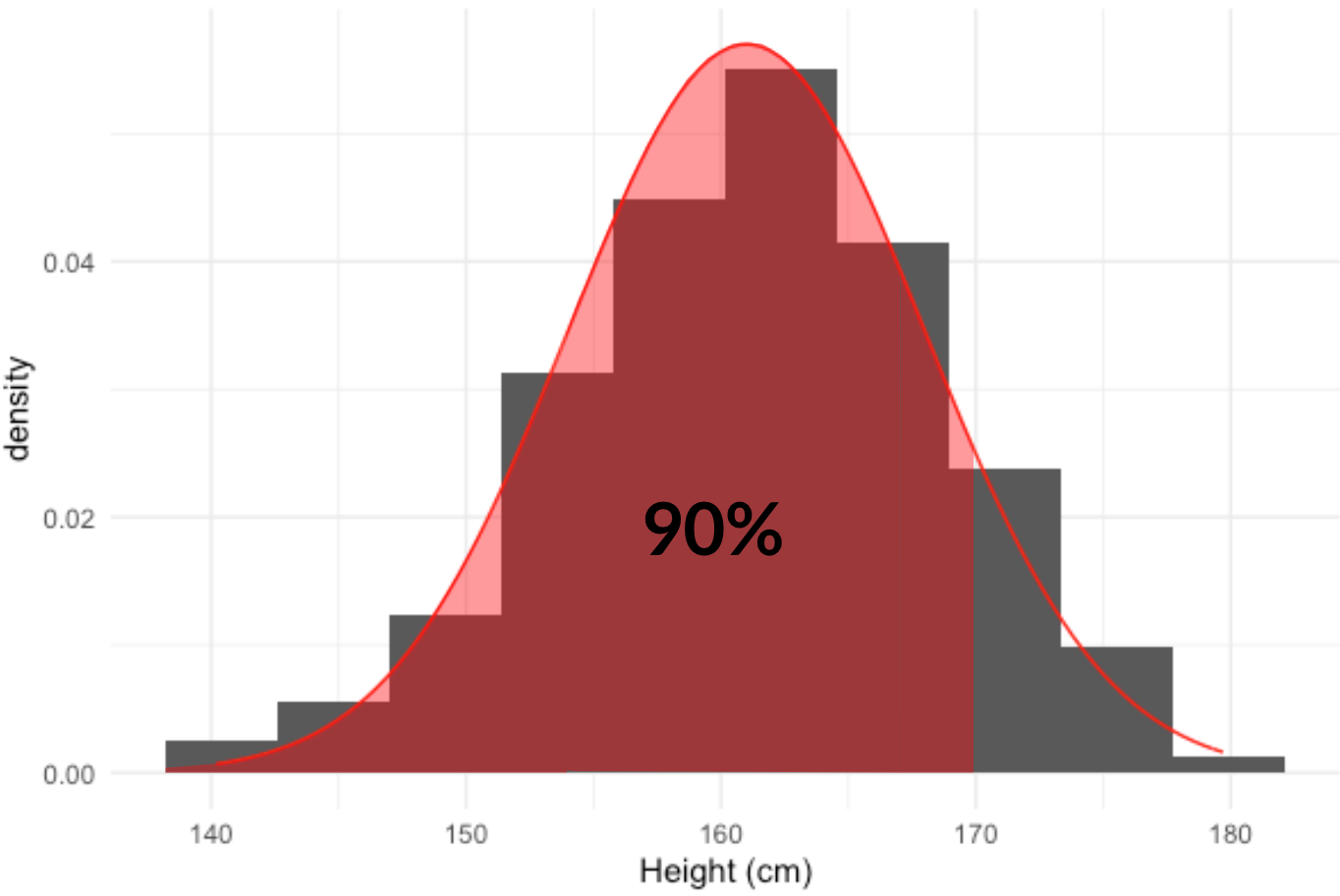
Zone inférieure à 170 ombrée, étiquetée avec 90 %.

qnorm(0.9, mean = 161, sd = 7)

169.9709
Introduction aux statistiques en R

90 % des femmes mesurent plus de combien ?

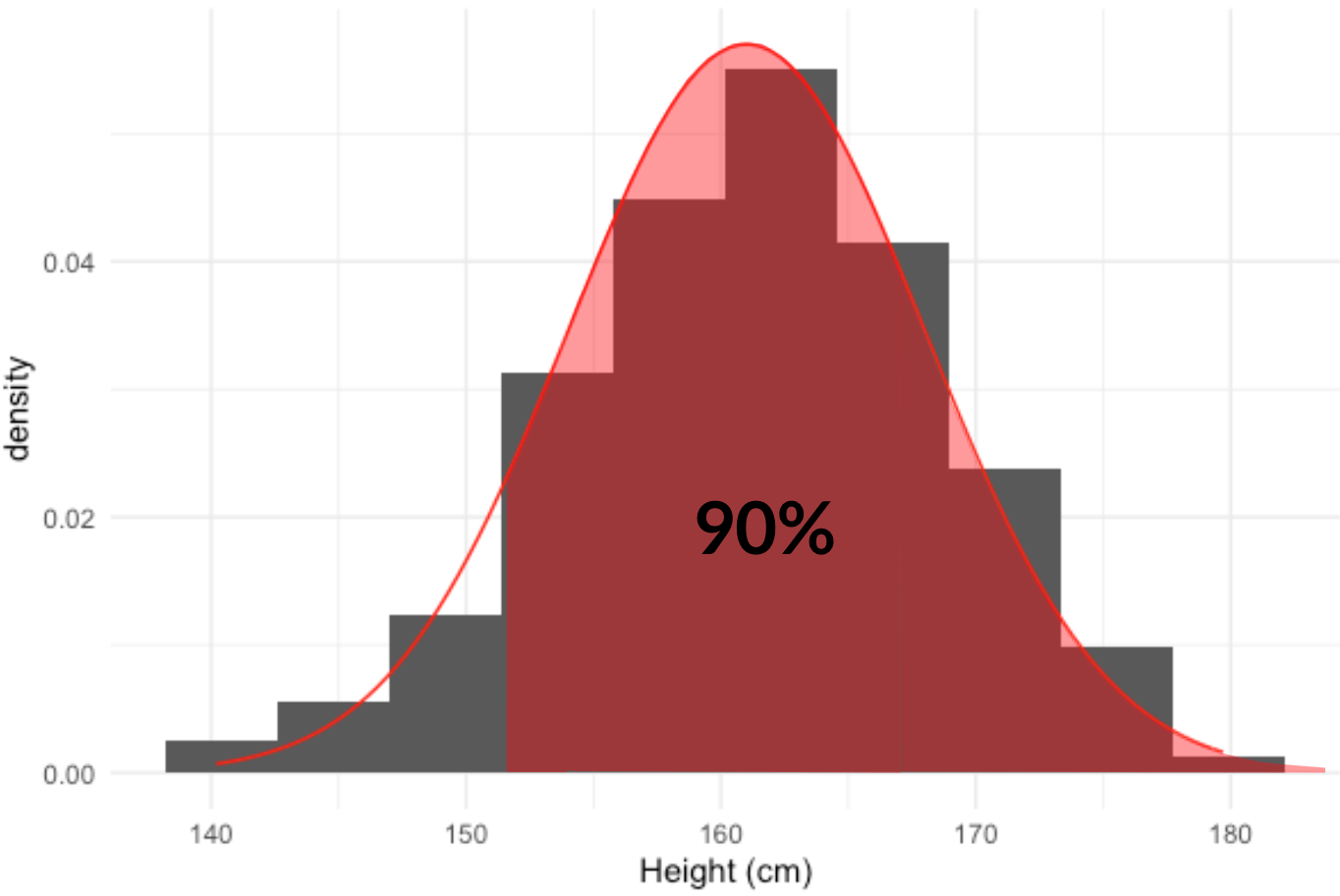
Zone supérieure à environ 162 ombrée, étiquetée avec 90 %.

qnorm(0.9,
      mean = 161,
      sd = 7,
      lower.tail = FALSE)

152.03
Introduction aux statistiques en R

Générer des nombres aléatoires

# Generate 10 random heights
rnorm(10, mean = 161, sd = 7)

159.35 157.34 149.85 156.75 163.53 156.33 157.22 171.44 158.10 170.12
Introduction aux statistiques en R

Passons à la pratique !

Introduction aux statistiques en R

Preparing Video For Download...