Le théorème de la limite centrale

Introduction aux statistiques en R

Maggie Matsui

Content Developer, DataCamp

Lancer un dé 5 fois

die <- c(1, 2, 3, 4, 5, 6)

# Roll 5 times
sample_of_5 <- sample(die, 5,
                      replace = TRUE)
sample_of_5

1 3 4 1 1

mean(sample_of_5)

2.0

 

dé à six faces

Introduction aux statistiques en R

Lancer un dé 5 fois

# Roll 5 times and take mean
sample(die, 5, replace = TRUE) %>% mean()

4.4

sample(die, 5, replace = TRUE) %>% mean()

3.8
Introduction aux statistiques en R

Lancer cinq fois les dés, dix fois

Répétez 10 fois :

  • Lancer 5 fois le dé
  • Prendre la moyenne

 

sample_means <- replicate(10, sample(die, 5, replace = TRUE) %>% mean())

sample_means

3.8 4.0 3.8 3.6 3.2 4.8 2.6 3.0 2.6 2.0
Introduction aux statistiques en R

Distributions d’échantillonnage

Distribution d’échantillonnage de la moyenne des échantillons

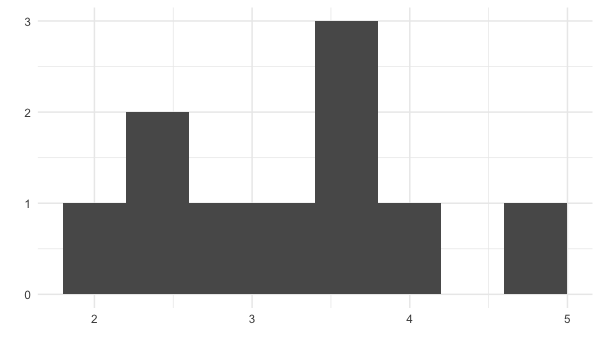
Histogramme des moyennes de 10 échantillons

Introduction aux statistiques en R

Les moyennes de 100 échantillons

replicate(100, sample(die, 5, replace = TRUE) %>% mean())

2.8 3.2 1.8 4.6 4.0 2.8 4.4 2.4 3.4 2.8 4.2 3.4 ... 2.2 3.8 3.6 3.8 4.4 4.8 2.4

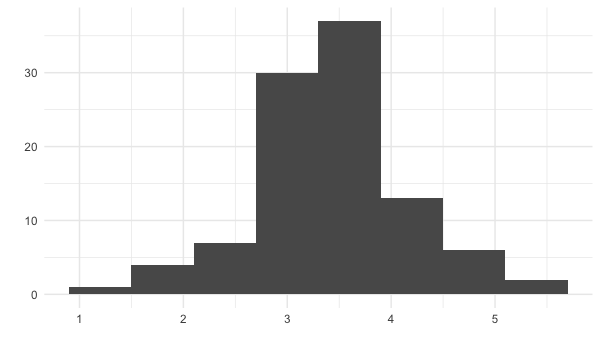
Histogramme des moyennes de 100 échantillons

Introduction aux statistiques en R

Les moyennes de 1 000 échantillons

sample_means <- replicate(1000, sample(die, 5, replace = TRUE) %>% mean())

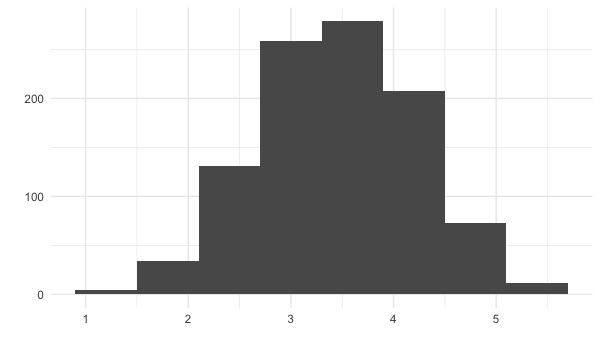
Histogramme des moyennes de 1 000 échantillons

Introduction aux statistiques en R

Théorème de la limite centrale

La distribution d’échantillonnage d’une statistique se rapproche de la distribution normale lorsque le nombre d’essais augmente.

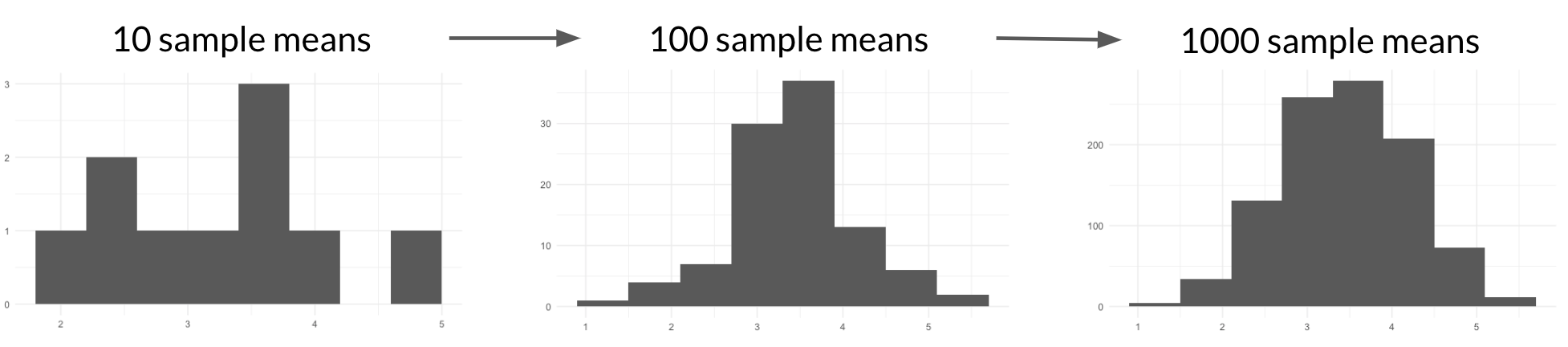
histogrammes de 10, 100 et 1000 moyennes d’échantillon, où un nombre plus élevé de moyennes d’échantillons a une distribution plus en forme de cloche

 

  • Les échantillons doivent être aléatoires et indépendants
Introduction aux statistiques en R

L’écart-type et le théorème de la limite centrale

replicate(1000, sample(die, 5, replace = TRUE) %>% sd())

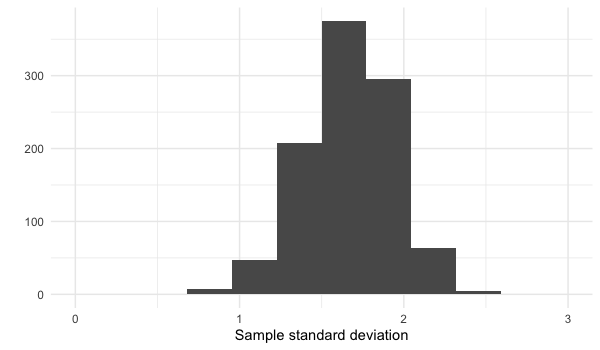
Distribution de 1 000 écarts-types d’échantillons de 5 lancers de dé

Introduction aux statistiques en R

Les proportions et le théorème de la limite centrale

sales_team <- c("Amir", "Brian", "Claire", "Damian")

sample(sales_team, 10, replace = TRUE)

"Claire" "Brian"  "Brian"  "Brian"  "Damian" "Damian" "Brian"  "Brian" 
"Amir"   "Amir"

sample(sales_team, 10, replace = TRUE)

"Amir"   "Amir"   "Claire" "Amir"   "Amir"   "Brian"  "Amir"   "Claire" 
"Claire" "Claire"
Introduction aux statistiques en R

Distribution d’échantillonnage de la proportion

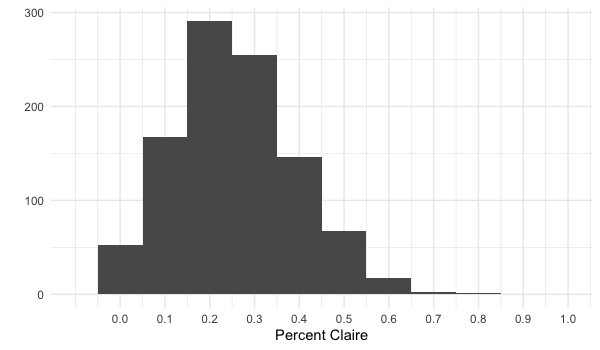
La distribution des proportions de l’échantillon semble également normale

Introduction aux statistiques en R

Moyenne de la distribution d’échantillonnage

# Estimate expected value of die
mean(sample_means)

3.48

# Estimate proportion of "Claire"s
mean(sample_props)

0.26
  • Estimer les caractéristiques d’une distribution sous-jacente inconnue

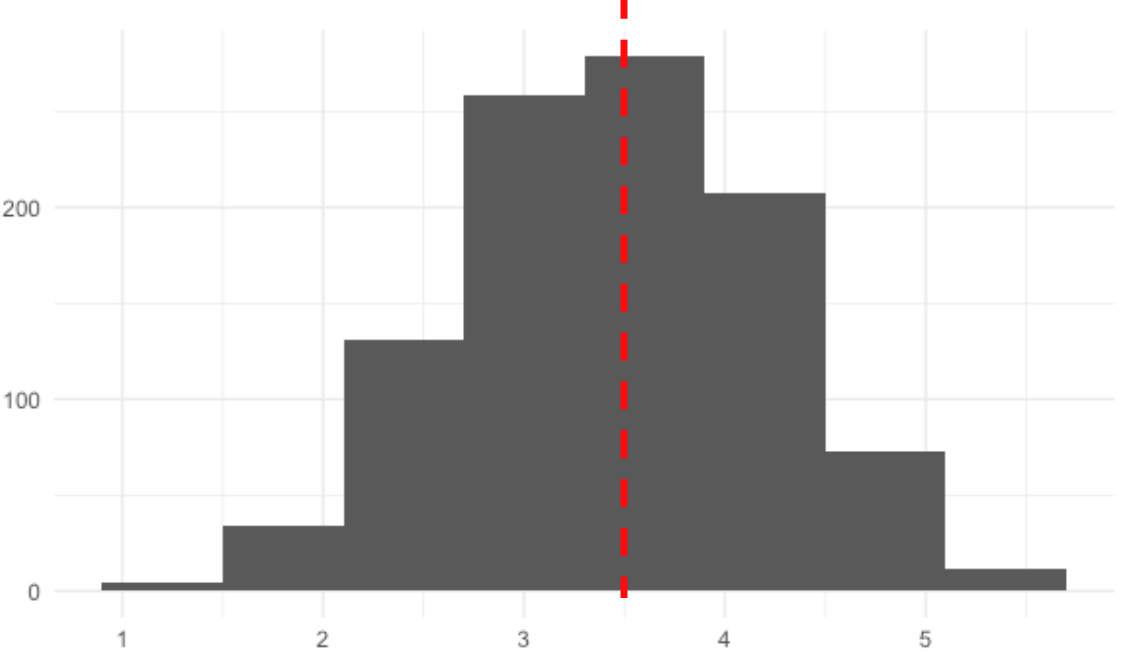
Distribution d’échantillonnage des moyennes des échantillons avec une ligne pointillée au milieu  

  • Estimer plus facilement les caractéristiques de grandes populations
Introduction aux statistiques en R

Passons à la pratique !

Introduction aux statistiques en R

Preparing Video For Download...