Quelles sont les chances ?

Introduction aux statistiques en R

Maggie Matsui

Content Developer, DataCamp

Mesurer les chances

Quelle est la probabilité d’un événement ?

$$ P(\text{event}) = \frac{\text{\# ways event can happen}}{\text{total \# of possible outcomes}} $$

Exemple : pile ou face

$$ P(\text{heads}) = \frac{\text{1 way to get heads}}{\text{2 possible outcomes}} = \frac{1}{2} = 50\%$$

Ligne numérique de probabilité. 0 % = impossible, 100 % = se produira certainement

Introduction aux statistiques en R

Affectation des vendeurs

Boîte avec les noms d’Amir, Brian, Claire et Damian

Introduction aux statistiques en R

Affectation des vendeurs

On tire le nom de Brian

$$P(\text{Brian}) = \frac{1}{4} = 25\%$$

Introduction aux statistiques en R

Échantillonnage à partir d'un DataFrame

sales_counts

   name  n_sales
 1 Amir      178
 2 Brian     126
 3 Claire     75
 4 Damian     69

sales_counts %>%
  sample_n(1)

   name  n_sales
 1 Brian     126

sales_counts %>%
  sample_n(1)

   name  n_sales
 1 Claire     75
Introduction aux statistiques en R

Définition d’une graine aléatoire

set.seed(5)

sales_counts %>%
  sample_n(1)

   name  n_sales
 1 Brian     126

set.seed(5)

sales_counts %>%
  sample_n(1)

   name  n_sales
 1 Brian     126
Introduction aux statistiques en R

Une deuxième réunion

Échantillonnage sans remise

Boîte avec Amir, Claire, Damian

Introduction aux statistiques en R

Une deuxième réunion

Le nom de Claire a été retiré

$$P(\text{Claire}) = \frac{1}{3} = 33\%$$

Introduction aux statistiques en R

Effectuer deux échantillonnages dans R

sales_counts %>%
  sample_n(2)

   name  n_sales
 1 Brian     126
 2 Claire     75
Introduction aux statistiques en R

Échantillonnage avec remise

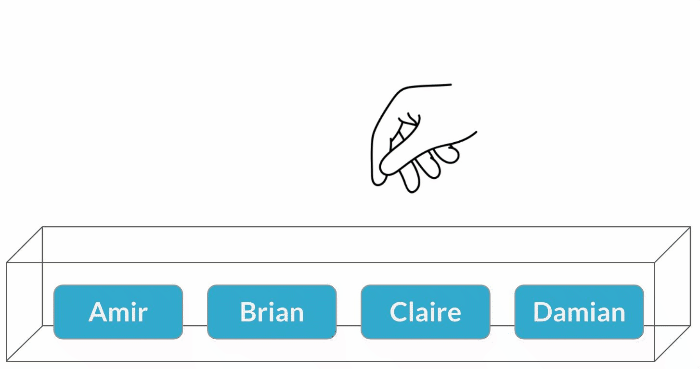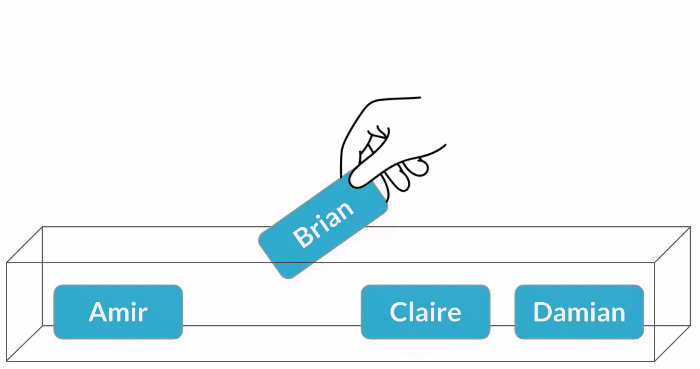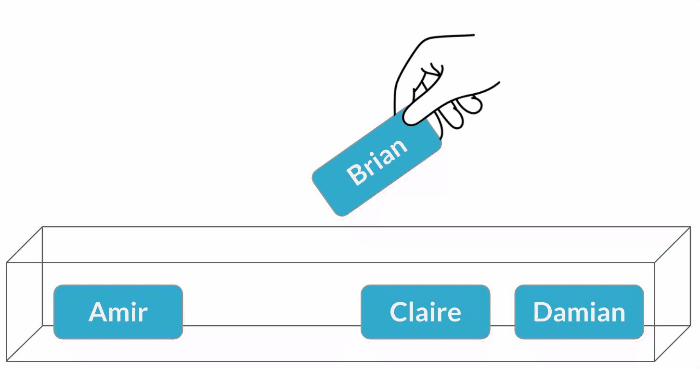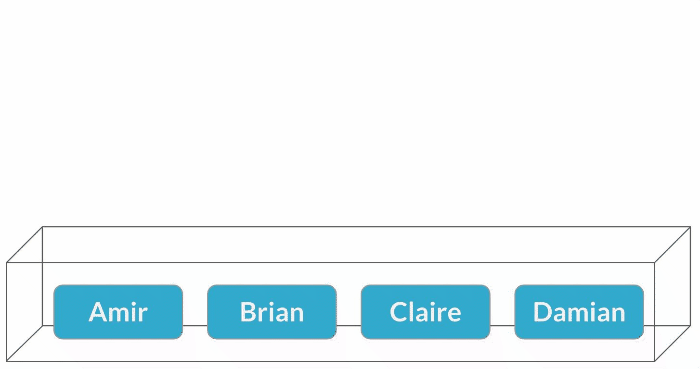
GIF d’une main plongeant dans la boîte, qui sort le nom de Brian, puis le remet dans la boîte

Introduction aux statistiques en R

Échantillonnage avec remise

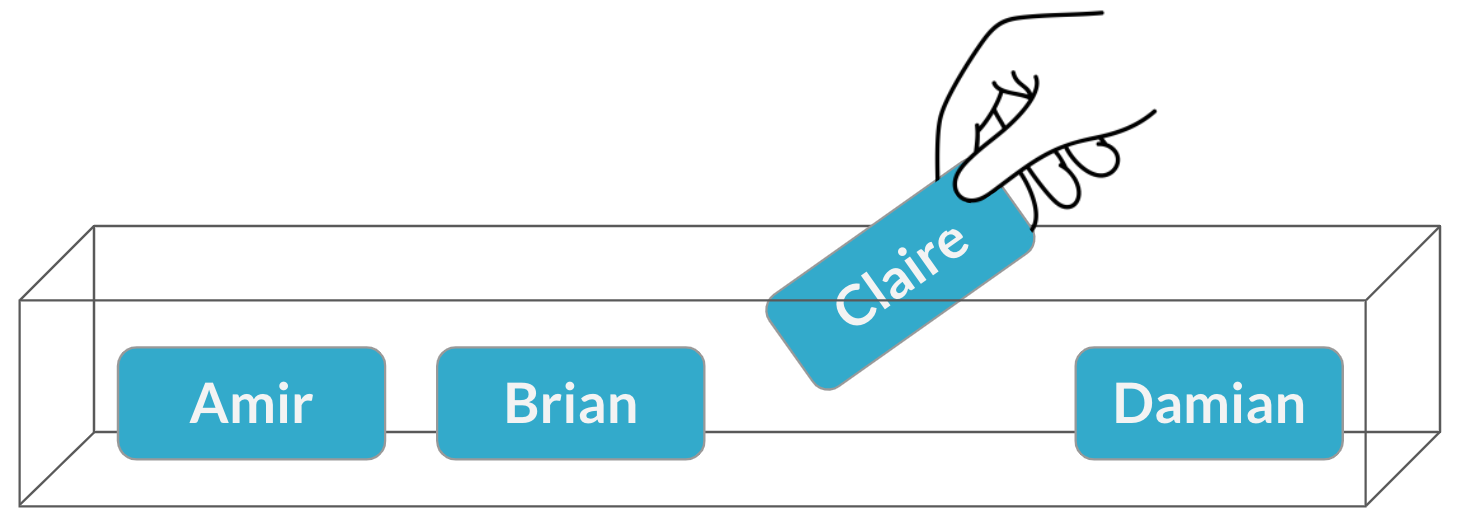
Screen Shot 2020-04-28 at 5.21.54 PM.png

$$P(\text{Claire}) = \frac{1}{4} = 25\%$$

Introduction aux statistiques en R

Échantillonnage avec remplacement dans R

sales_counts %>%
  sample_n(2, replace = TRUE)

   name  n_sales
 1 Brian     126
 2 Claire     75

Cinq réunions :

sample(sales_team, 5, replace = TRUE)

   name  n_sales
 1 Brian     126
 2 Claire     75
 3 Brian     126
 4 Brian     126
 5 Amir      178
Introduction aux statistiques en R

Événements indépendants

Deux événements sont indépendants si la probabilité du deuxième événement n’est pas affectée par le résultat du premier.

Deux colonnes : Colonne de premier choix contenant Amir, Brian, Claire, Damian. La colonne de deuxième choix est vide

Introduction aux statistiques en R

Événements indépendants

Deux événements sont indépendants si la probabilité du deuxième événement n’est pas affectée par le résultat du premier.

 

Échantillonnage avec remise : chaque choix est indépendant

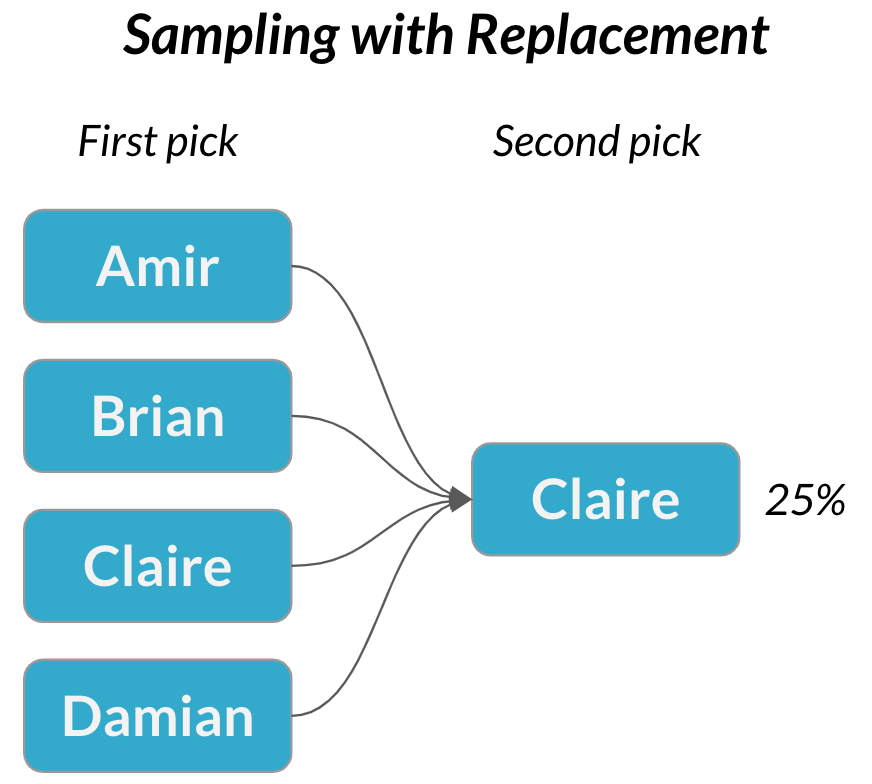
Les flèches partant de chaque nom dans la première colonne de sélection pointent vers Claire dans la deuxième colonne de sélection, avec une probabilité de 25 %

Introduction aux statistiques en R

Événements dépendants

Deux événements sont dépendants si la probabilité du deuxième événement est affectée par le résultat du premier.

Deux colonnes : Colonne de premier choix contenant Amir, Brian, Claire, Damian. La colonne de deuxième choix est vide

Introduction aux statistiques en R

Événements dépendants

Deux événements sont dépendants si la probabilité du deuxième événement est affectée par le résultat du premier.

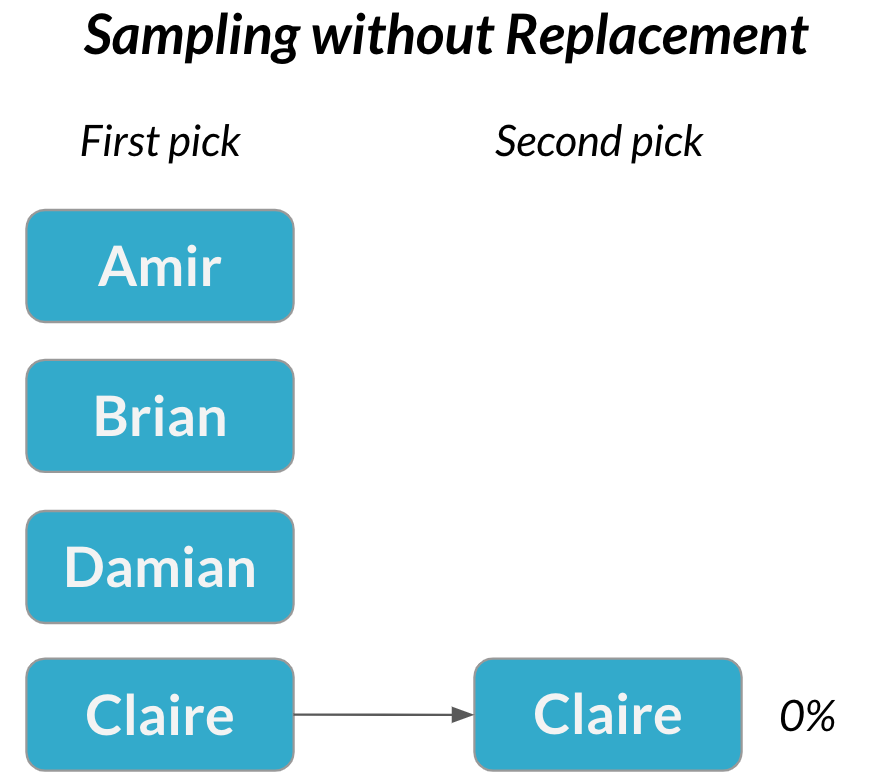
Claire dans la première colonne pointe vers Claire dans la deuxième colonne avec une probabilité de 0 %

Introduction aux statistiques en R

Événements dépendants

Deux événements sont dépendants si la probabilité du deuxième événement est affectée par le résultat du premier.

 

Échantillonnage sans remplacement = chaque sélection est dépendante

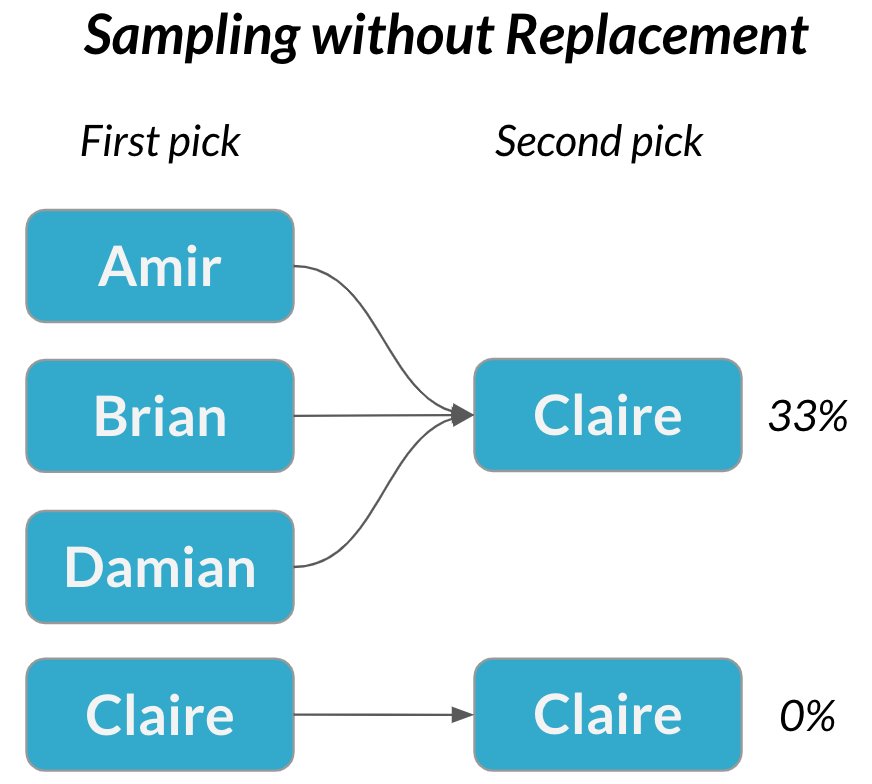
Amir, Brian et Damian dans la première colonne pointent vers Claire dans la deuxième colonne avec une probabilité de 33 %

Introduction aux statistiques en R

Passons à la pratique !

Introduction aux statistiques en R

Preparing Video For Download...