Découverte des fonctions d’activation

Introduction au deep learning avec PyTorch

Jasmin Ludolf

Senior Data Science Content Developer, DataCamp

Fonctions d’activation

Les fonctions d’activation ajoutent de la non-linéarité au réseau
- Sigmoïde pour la classification binaire
- Softmax pour la classification multi-classes
Un réseau peut apprendre des relations plus complexes grâce à la non-linéarité
Sortie « pré-activation » transmise à la fonction d’activation

Schéma d’un réseau neuronal avec des couches linéaires et une fonction d’activation

Découvrez la fonction sigmoïde

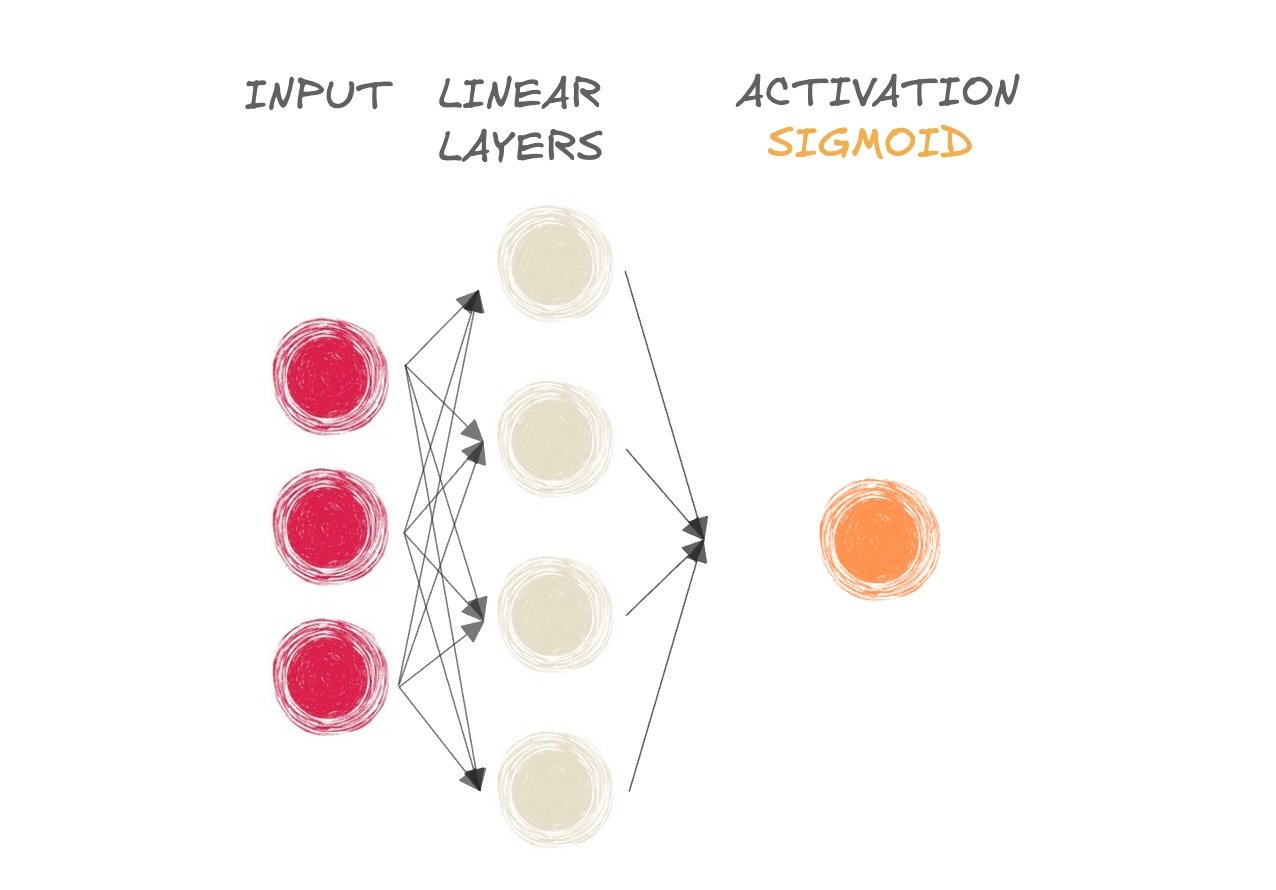
Schéma d’une partie d’un réseau neuronal avec entrée, couches linéaires et fonction d’activation

Mammifère ou pas ?

Illustration d’un lémurien

Découvrez la fonction sigmoïde

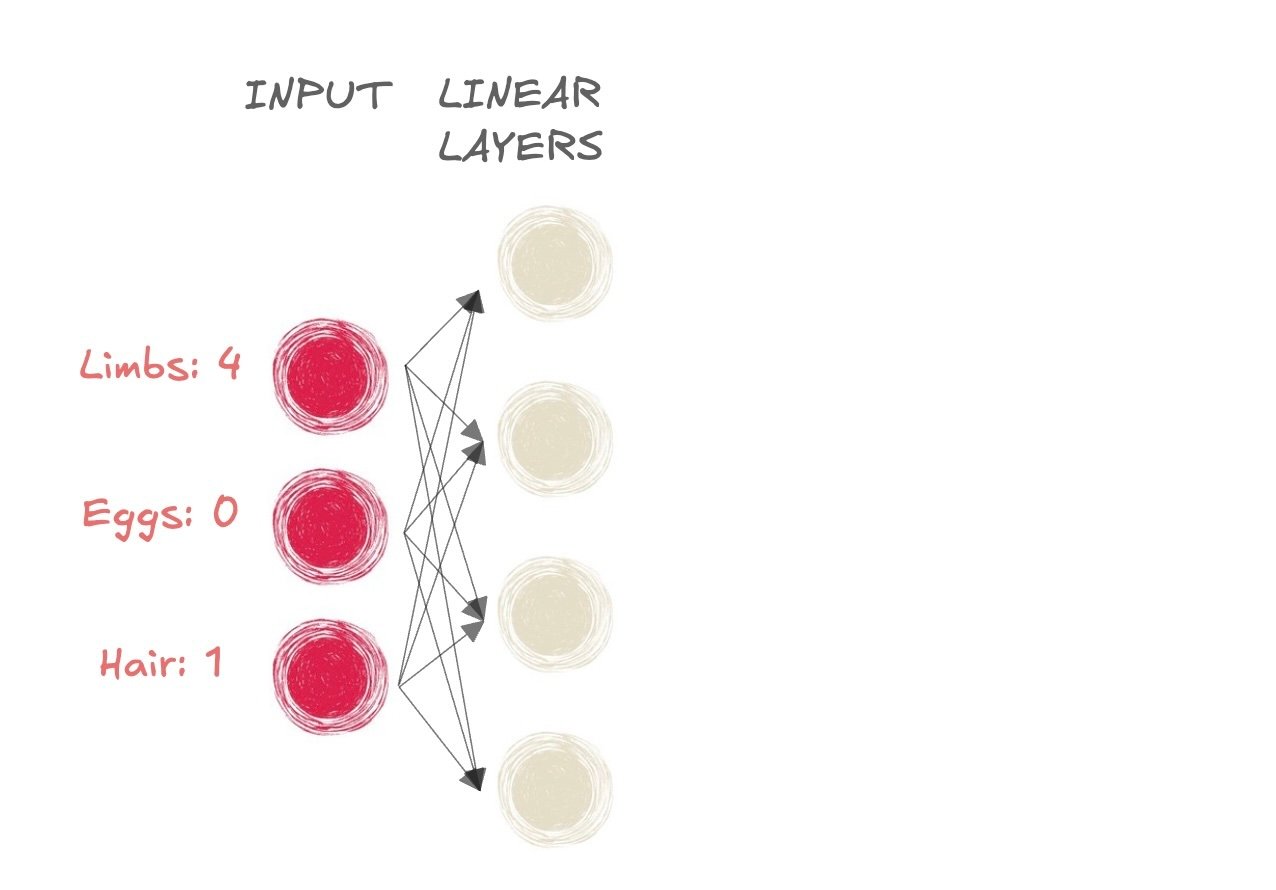
Schéma d’une partie d’un réseau neuronal avec des entrées et des couches linéaires

Mammifère ou pas ?

Illustration d’un lémurien

Entrée :
- Membres : 4
- Œufs : 0
- Poils : 1

Découvrez la fonction sigmoïde

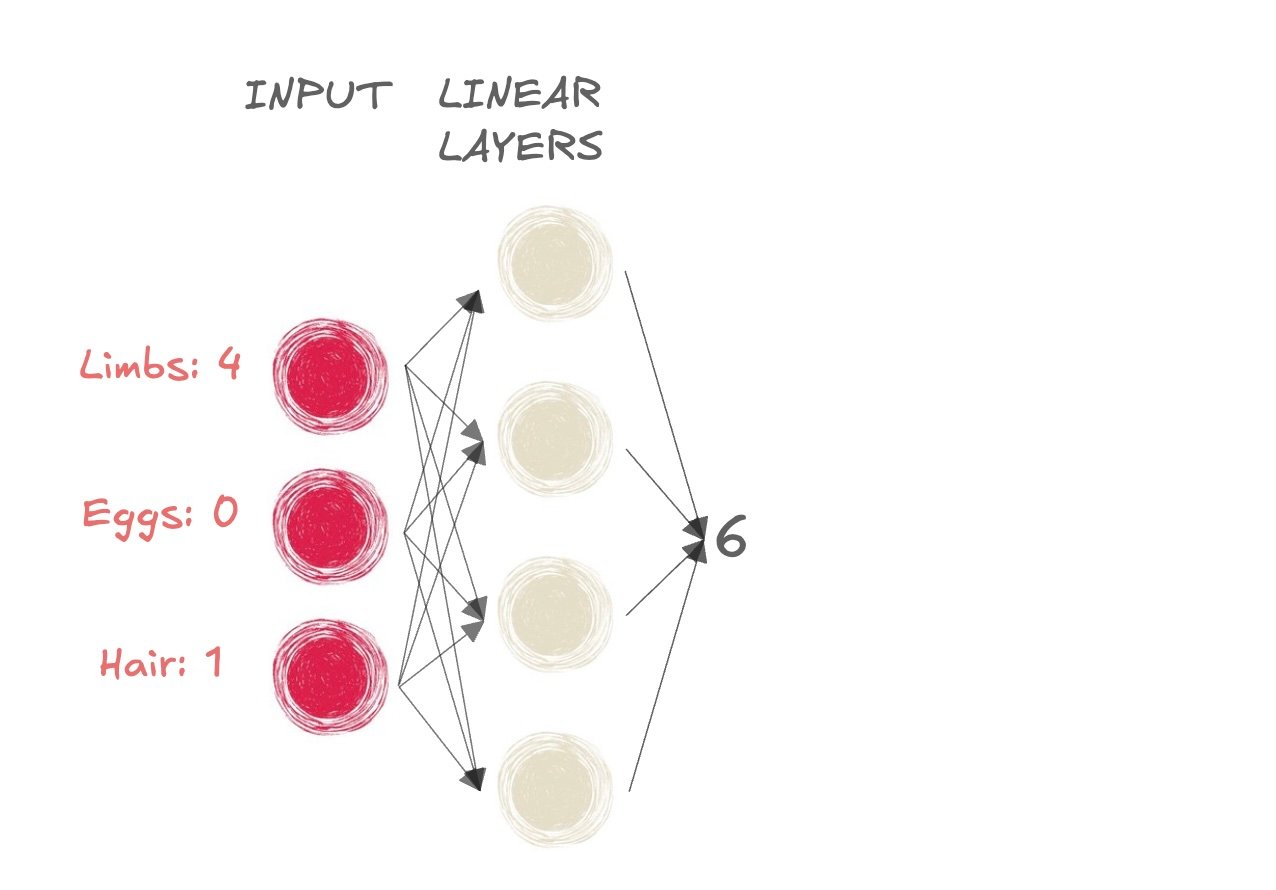
Schéma d’une partie d’un réseau neuronal avec des entrées et le chiffre 6 en sortie des couches linéaires

Mammifère ou pas ?

Illustration d’un lémurien

La sortie des couches linéaires est 6

Découvrez la fonction sigmoïde

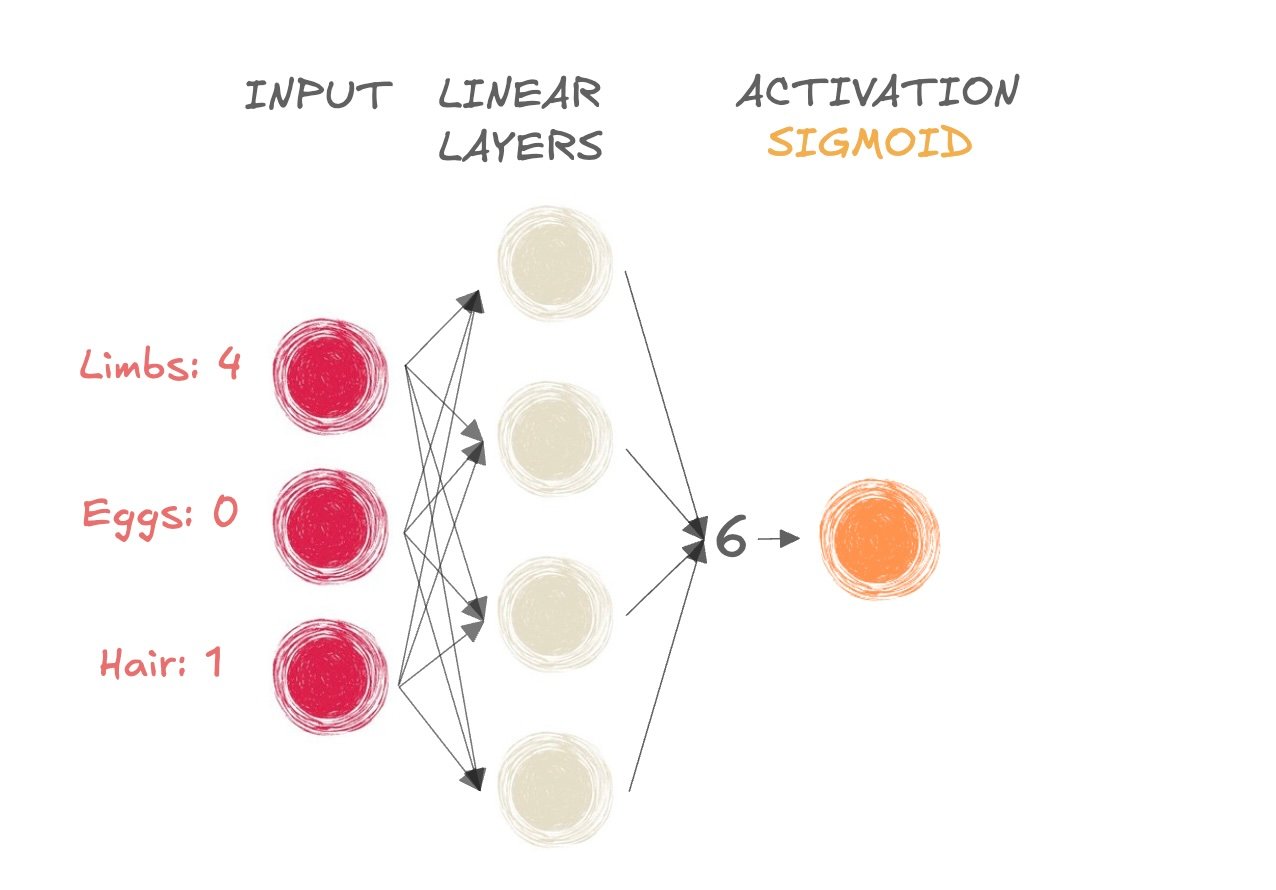
Schéma d’une partie d’un réseau neuronal avec des entrées, le chiffre 6 en sortie des couches linéaires, et une fonction d’activation sigmoïde

Mammifère ou pas ?

Illustration d’un lémurien

Nous prenons la sortie de pré-activation (6) et la passons à la fonction sigmoïde

Découvrez la fonction sigmoïde

Schéma d’une partie d’un réseau neuronal avec des entrées, le chiffre 6 en sortie des couches linéaires, une fonction d’activation sigmoïde et une sortie

Mammifère ou pas ?

Illustration d’un lémurien

Nous prenons la sortie de pré-activation (6) et la passons à la fonction sigmoïde
Obtenir une valeur entre 0 et 1
Résultat > 0,5 → classe 1 (mammifère)
Résultat ≤ 0,5 → classe 0 (pas un mammifère)

Découvrez la fonction sigmoïde

import torch
import torch.nn as nn

input_tensor = torch.tensor([[6]])
sigmoid = nn.Sigmoid()

output = sigmoid(input_tensor)
print(output)

tensor([[0.9975]])

L’activation comme dernière couche

model = nn.Sequential(
  nn.Linear(6, 4), # First linear layer
  nn.Linear(4, 1), # Second linear layer
  nn.Sigmoid() # Sigmoid activation function
)

La sigmoïde en dernière étape d’un réseau de couches linéaires est équivalente à la régression logistique classique.

Se familiariser avec softmax

Trois classes :

Se familiariser avec softmax

Trois classes :

Un lémurien avec l’option « oiseau »

Se familiariser avec softmax

Trois classes :

Un lémurien avec les options « oiseau » et « mammifère »

Se familiariser avec softmax

Trois classes :

Un lémurien avec trois options : « oiseau », « mammifère » ou « reptile »

Se familiariser avec softmax

Schéma d’une partie d’un réseau neuronal avec des entrées

Prend une forme tridimensionnelle en entrée et produit la même forme en sortie

Se familiariser avec softmax

Schéma d’une partie d’un réseau neuronal avec des entrées, un vecteur en sortie des couches linéaires, une fonction d’activation softmax et une sortie

Prend une forme tridimensionnelle en entrée et produit la même forme en sortie
Produit une distribution de probabilités :
- Chaque élément est une probabilité (comprise entre 0 et 1)
- La somme du vecteur de sortie est égale à 1

Se familiariser avec softmax

Schéma d’une partie d’un réseau neuronal avec des entrées, un vecteur en sortie des couches linéaires, une fonction d’activation softmax et une sortie

Prend une forme tridimensionnelle en entrée et produit la même forme en sortie
Produit une distribution de probabilités :
- Chaque élément est une probabilité (comprise entre 0 et 1)
- La somme du vecteur de sortie est égale à 1

Se familiariser avec softmax

import torch
import torch.nn as nn

# Create an input tensor
input_tensor = torch.tensor(
    [[4.3, 6.1, 2.3]])

# Apply softmax along the last dimension

probabilities = nn.Softmax(dim=-1)
output_tensor = probabilities(input_tensor)
print(output_tensor)

tensor([[0.1392, 0.8420, 0.0188]])

dim = -1 indique qu’une fonction softmax est appliquée à la dernière dimension du tenseur d’entrée
nn.Softmax() peut être utilisé comme dernière étape dans nn.Sequential()

Passons à la pratique !

Introduction au deep learning avec PyTorch