Choosing probability distributions

Monte Carlo Simulations in Python

Izzy Weber

Curriculum Manager, DataCamp

Maximum Likelihood Estimation (MLE)

Used to select a probability distribution by measuring fit
- Distribution yielding highest likelihood given the data is considered optimal
SciPy's .nnlf() used to calculate the negative likelihood function
The lower the MLE value calculated using .nnlf(), the better the fit

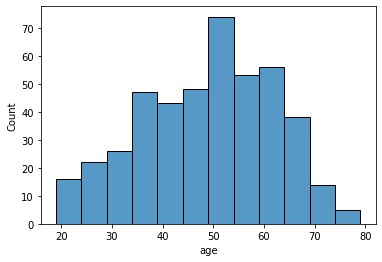
Picking a distribution for the age variable

sns.histplot(dia["age"])

A histogram of the distribution of the age variable from the diabetes dataset

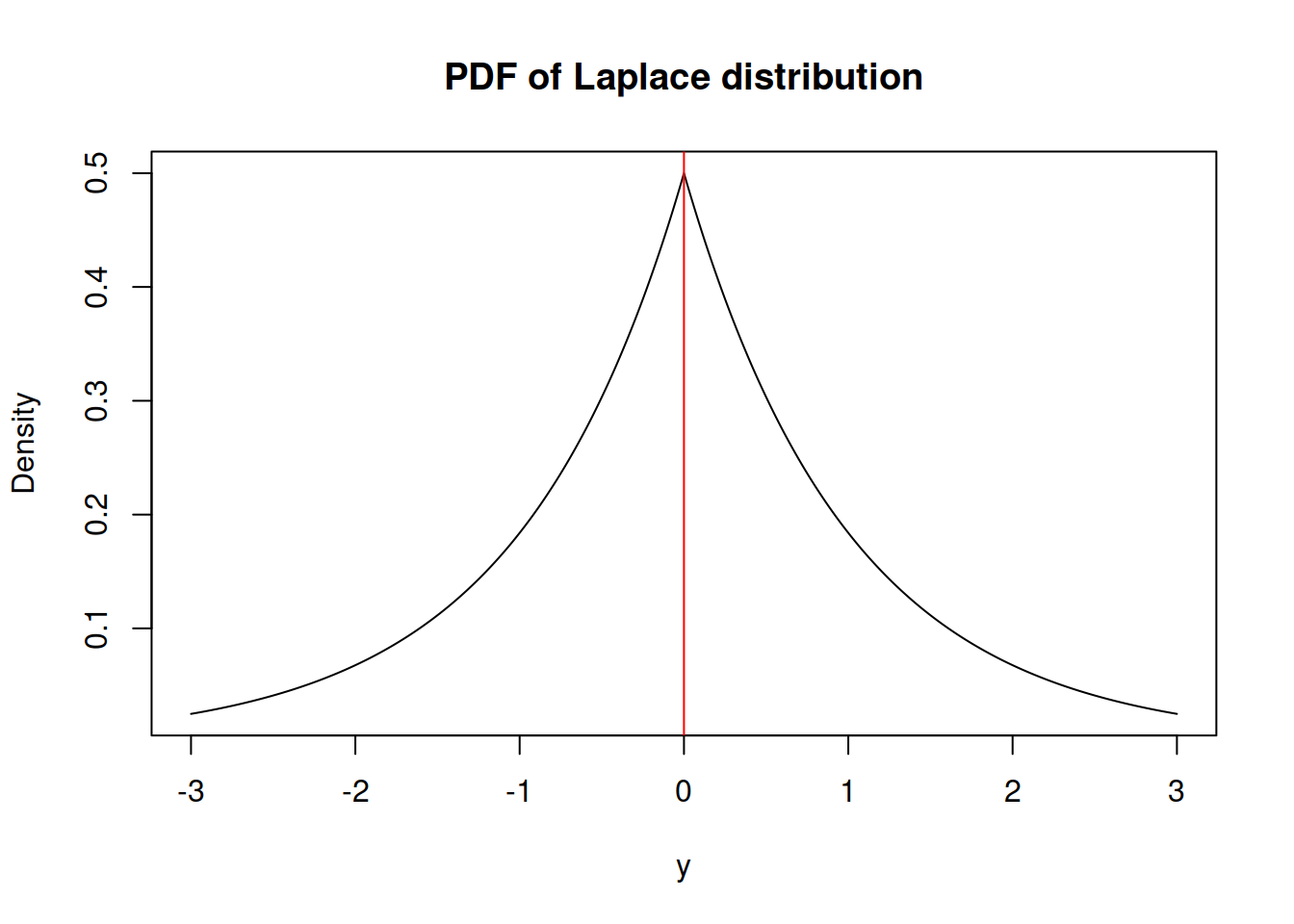
Candidate distributions

distributions = [st.laplace, st.norm, st.expon]

A PDF of the laplace distribution

Choosing between candidate distributions

mles = []


for distribution in distributions:
    pars = distribution.fit(dia["age"])

    mle = distribution.nnlf(pars, dia["age"])

    mles.append(mle)


print(mles)

[1797.8467779878652, 1764.0693689033028, 1938.171599681118]

Choosing between candidate distributions

for var in ["age", "bmi", "bp", "tc", "ldl", "hdl", "tch", "ltg", "glu"]:

    distributions = [st.laplace, st.norm, st.expon]
    mles = []


    for distribution in distributions:
        pars = distribution.fit(dia[var])
        mle = distribution.nnlf(pars, dia[var])
        mles.append(mle)


    best_fit = sorted(zip(distributions, mles), key=lambda d: d[1])[0]
    print(f"Best fit reached using {best_fit[0].name}, \
          MLE value: {best_fit[1]}, for variable {var}")

Results of the evaluation

Best fit reached using norm, MLE value: 1764.0693689033028, for variable age
Best fit reached using norm, MLE value: 1283.356127017369, for variable bmi
Best fit reached using norm, MLE value: 1787.7746251622739, for variable bp
Best fit reached using norm, MLE value: 2193.1564373753627, for variable to
Best fit reached using norm, MLE value: 2136.0440476305284, for variable ldl
Best fit reached using norm, MLE value: 1758.1350738323013, for variable hdl
Best fit reached using norm, MLE value: 739.3762494786798, for variable tch
Best fit reached using norm, MLE value: 339.6620870566908, for variable ltg
Best fit reached using norm, MLE value: 1706.0467588930867, for variable glu

Let's practice!

Monte Carlo Simulations in Python