The Monte Carlo process

Monte Carlo Simulations in Python

Izzy Weber

Curriculum Manager, DataCamp

Simulation steps

Define the input variables and pick probability distributions for them
Generate inputs by sampling from these distributions
Perform a deterministic calculation of the simulated inputs
Summarize results

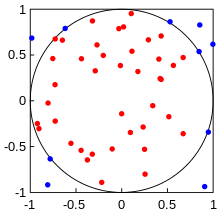
Calculating the value of pi

Generate random points $(x, y)$ where $x$ and $y$ are in the interval from -1 to 1.

A graph of a circle inside a square with randomly sampled points

$$Area_{circle} = \pi $$

$$Area_{square} = 2 \times 2 = 4 $$

$$\frac{Area_{circle}}{Area_{square}} = \frac{\pi}{4} $$

$$\frac{n_{red}}{n_{all}} = \frac{\pi}{4} $$

$$ \pi = 4 \times \frac{n_{red}}{n_{all}}$$

Step 1

Define the input variables and pick probability distributions for them

Inputs: the individual points represented by $(x, y)$ coordinates
Probability distributions: $x$ and $y$ follow uniform distributions from negative one to one.

circle_points = 0 
square_points = 0

Step 2

Generate inputs by sampling from these distributions

Sample random $x$ and $y$ coordinate values distributed uniformly between -1 and 1:

for i in range(n):
    x = random.uniform(-1, 1)
    y = random.uniform(-1, 1)

Step 3

Perform deterministic calculation of the simulated inputs

Check whether each point lies within the circle: deterministic for given $x$ and $y$

dist_from_origin = x**2 + y**2

If yes, add the point to circle_points; always add the point to square_points

if dist_from_origin <= 1:
     circle_points += 1
square_points += 1

Step 4

Summarize the results to answer questions of interest

After many rounds of simulations, calculate the value of pi!

pi = 4 * circle_points/ square_points

All together now

n = 4000000
circle_points = 0 
square_points = 0

for i in range(n):
    x = random.uniform(-1, 1)
    y = random.uniform(-1, 1)
    dist_from_origin = x**2 + y**2
    if dist_from_origin <= 1:
        circle_points += 1
    square_point += 1

pi = 4 * circle_points / square_points
print(pi)

3.142518

Let's practice!

Monte Carlo Simulations in Python