Régression vers la moyenne

Introduction à la régression avec statsmodels en Python

Maarten Van den Broeck

Content Developer at DataCamp

Le concept

  • Valeur de réponse = valeur ajustée + résidu
  • « Ce que vous avez expliqué » + « ce que vous n'avez pas pu expliquer »
  • Les résidus sont présents en raison de problèmes dans le modèle et du caractère aléatoire fondamental.
  • Les cas extrêmes sont souvent dus au hasard.
  • La régression vers la moyenne implique que les cas extrêmes ne persistent pas dans le temps.
Introduction à la régression avec statsmodels en Python

Ensemble de données père-fils de Pearson

  • 1 078 paires père/fils
  • Les pères de grande taille ont-ils des fils de grande taille ?
father_height_cm son_height_cm
165,2 151,8
160,7 160,6
165,0 160,9
167,0 159,5
155,3 163,3
... ...
1 Adapté de https://www.rdocumentation.org/packages/UsingR/topics/father.son
Introduction à la régression avec statsmodels en Python

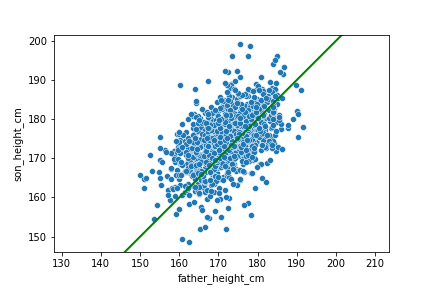
Diagramme de dispersion

fig = plt.figure()

sns.scatterplot(x="father_height_cm",
                y="son_height_cm",
                data=father_son)

plt.axline(xy1=(150, 150),
           slope=1,
           linewidth=2,
           color="green")

plt.axis("equal")
plt.show()

Un diagramme en nuage de points représentant la taille des fils par rapport à celle des pères, avec une ligne indiquant les cas où le père et le fils auraient la même taille. Plus les pères sont grands, plus les fils le sont aussi.

Introduction à la régression avec statsmodels en Python

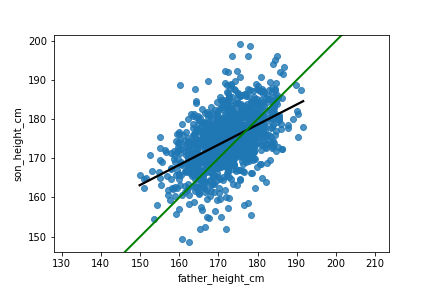
Ajout d'une ligne de régression

fig = plt.figure()

sns.regplot(x="father_height_cm",
            y="son_height_cm",
            data=father_son,
            ci = None, 
            line_kws={"color": "black"})

plt.axline(xy1 = (150, 150),
           slope=1,
           linewidth=2,
           color="green")

plt.axis("equal")
plt.show()

Le diagramme en nuage de points représentant la taille des fils par rapport à celle des pères, accompagné d'une courbe de tendance linéaire. La courbe est moins pentue que celle où les pères et les fils auraient la même taille.

Introduction à la régression avec statsmodels en Python

Effectuer une régression

mdl_son_vs_father = ols("son_height_cm ~ father_height_cm",
                        data = father_son).fit()
print(mdl_son_vs_father.params)

Intercept           86.071975
father_height_cm     0.514093
dtype: float64
Introduction à la régression avec statsmodels en Python

Faire des prévisions

really_tall_father = pd.DataFrame(
  {"father_height_cm": [190]})

mdl_son_vs_father.predict(
  really_tall_father)

183.7

really_short_father = pd.DataFrame(
  {"father_height_cm": [150]})

mdl_son_vs_father.predict(
  really_short_father)

163.2
Introduction à la régression avec statsmodels en Python

Passons à la pratique !

Introduction à la régression avec statsmodels en Python

Preparing Video For Download...