Quantification de l'ajustement du modèle

Introduction à la régression avec statsmodels en Python

Maarten Van den Broeck

Content Developer at DataCamp

Modèles de brèmes communes et de perches

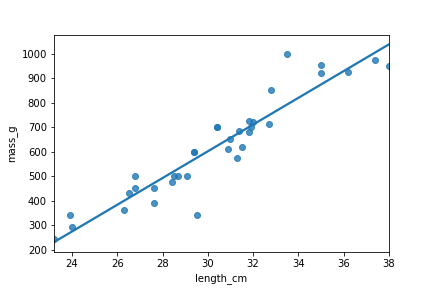
Brème commune Le diagramme en nuage de points représentant le rapport entre la masse et la longueur des brèmes communes, avec une courbe de tendance, qui a été présenté précédemment.

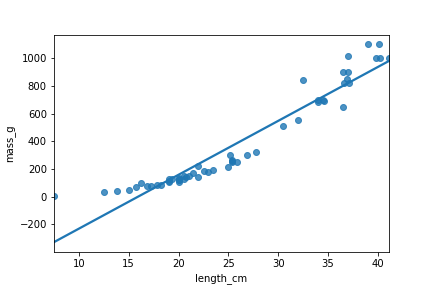
Perche Le diagramme en nuage de points représentant le poids des perches en fonction de leur longueur, avec une courbe de tendance, qui a été présenté précédemment.

Introduction à la régression avec statsmodels en Python

Coefficient de détermination

Parfois appelé « r au carré » ou « R au carré ».

La proportion de la variance de la variable de réponse qui est prévisible à partir de la variable explicative

  • 1 signifie un ajustement parfait
  • 0 signifie le pire ajustement possible
Introduction à la régression avec statsmodels en Python

.summary()

Examiner la valeur intitulée « R au carré »

mdl_bream = ols("mass_g ~ length_cm", data=bream).fit()

print(mdl_bream.summary())

# Some lines of output omitted                          

                            OLS Regression Results                         
Dep. Variable:                 mass_g   R-squared:                       0.878
Model:                            OLS   Adj. R-squared:                  0.874
Method:                 Least Squares   F-statistic:                     237.6
Introduction à la régression avec statsmodels en Python

Attribut .rsquared

print(mdl_bream.rsquared)

0.8780627095147174
Introduction à la régression avec statsmodels en Python

Il s'agit simplement d'une corrélation au carré.

coeff_determination = bream["length_cm"].corr(bream["mass_g"]) ** 2
print(coeff_determination)

0.8780627095147173
Introduction à la régression avec statsmodels en Python

Erreur type résiduelle (ETR)

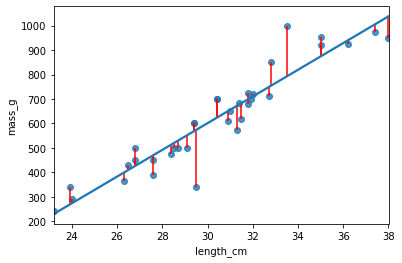
Résidus du graphique représentant la masse par rapport à la longueur des brèmes, comme indiqué précédemment

  • Une différence « typique » entre une prédiction et une réponse observée
  • Elle a la même unité que la variable de réponse.
  • MSE = RSE²
Introduction à la régression avec statsmodels en Python

Attribut .mse_resid

mse = mdl_bream.mse_resid
print('mse: ', mse)

mse:  5498.555084973521

rse = np.sqrt(mse)
print("rse: ", rse)

rse:  74.15224261594197
Introduction à la régression avec statsmodels en Python

Calcul du RSE : résidus au carré

residuals_sq = mdl_bream.resid ** 2

print("residuals sq: 
", residuals_sq)

residuals sq: 
0      138.957118
1      260.758635
2     5126.992578
3     1318.919660
4      390.974309
    ...
30    2125.047026
31    6576.923291
32     206.259713
33     889.335096
34    7665.302003
Length: 35, dtype: float64
Introduction à la régression avec statsmodels en Python

Calcul du RSE : somme des résidus au carré

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

print("resid sum of sq :",
      resid_sum_of_sq)

resid sum of sq : 181452.31780412616
Introduction à la régression avec statsmodels en Python

Calcul du RSE : degrés de liberté

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

deg_freedom = len(bream.index) - 2

print("deg freedom: ", deg_freedom)

Le nombre de degrés de liberté correspond au nombre d'observations moins le nombre de coefficients du modèle.

deg freedom:  33
Introduction à la régression avec statsmodels en Python

Calcul du RSE : racine carrée du rapport

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

deg_freedom = len(bream.index) - 2

rse = np.sqrt(resid_sum_of_sq/deg_freedom)

print("rse :", rse)

rse : 74.15224261594197
Introduction à la régression avec statsmodels en Python

Interprétation de la RSE

mdl_bream a un RSE de 74.

La différence entre les masses prévues et les masses observées pour les brèmes communes est généralement d'environ 74 g.

Introduction à la régression avec statsmodels en Python

Erreur quadratique moyenne (RMSE)

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

deg_freedom = len(bream.index) - 2

rse = np.sqrt(resid_sum_of_sq/deg_freedom)

print("rse :", rse)

rse : 74.15224261594197

residuals_sq = mdl_bream.resid ** 2

resid_sum_of_sq = sum(residuals_sq)

n_obs = len(bream.index)

rmse = np.sqrt(resid_sum_of_sq/n_obs)

print("rmse :", rmse)

rmse : 72.00244396727619
Introduction à la régression avec statsmodels en Python

Passons à la pratique !

Introduction à la régression avec statsmodels en Python

Preparing Video For Download...