Ajustement d'une régression linéaire

Introduction à la régression avec statsmodels en Python

Maarten Van den Broeck

Content Developer at DataCamp

Les lignes droites sont définies par deux éléments

Ordonnée à l’origine

La valeur $y$ au moment où $x$ est égal à zéro.

Pente

La valeur $y$ augmente d'autant si vous augmentez $x$ d'un point.

Équation

$y = \text{intercept} + \text{slope} * x$

Introduction à la régression avec statsmodels en Python

Estimation de l'ordonnée à l'origine

Un diagramme en nuage de points représentant le paiement total par rapport au nombre de réclamations, avec une courbe de tendance linéaire. Le paiement augmente de manière linéaire à mesure que le nombre de réclamations augmente.

Introduction à la régression avec statsmodels en Python

Estimation de l'ordonnée à l'origine

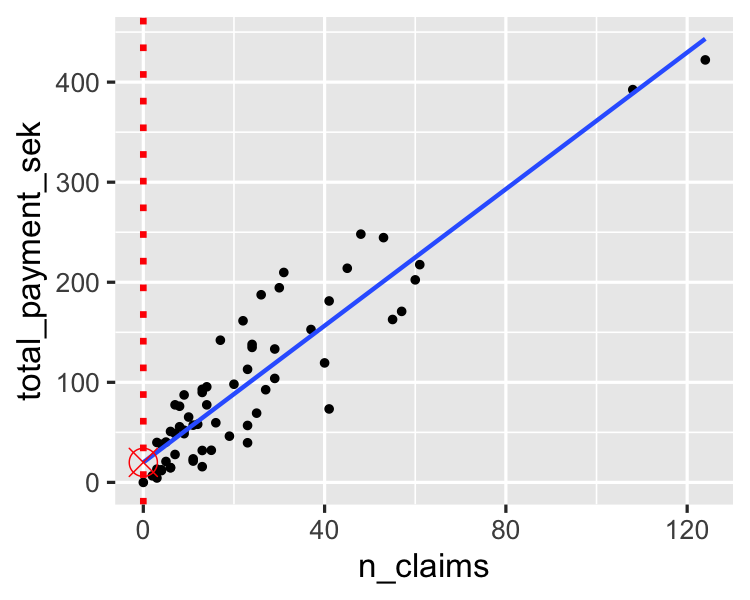
Le diagramme en nuage de points représentant le paiement total par rapport au nombre de réclamations, avec une annotation indiquant le point où la courbe de tendance croise l'axe des y.

Introduction à la régression avec statsmodels en Python

Estimation de l'ordonnée à l'origine

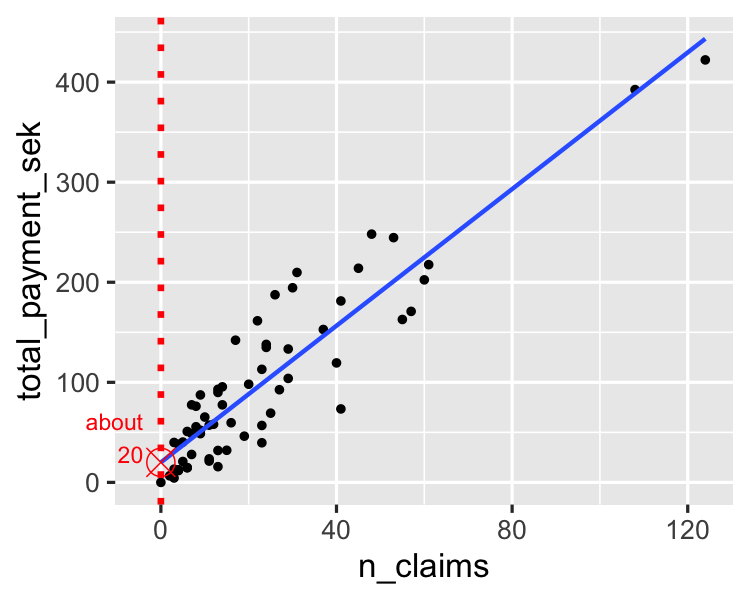
Le diagramme en nuage de points représentant le paiement total par rapport au nombre de réclamations, annoté avec la valeur lorsque le nombre de réclamations est égal à zéro.

Introduction à la régression avec statsmodels en Python

Évaluation de la pente

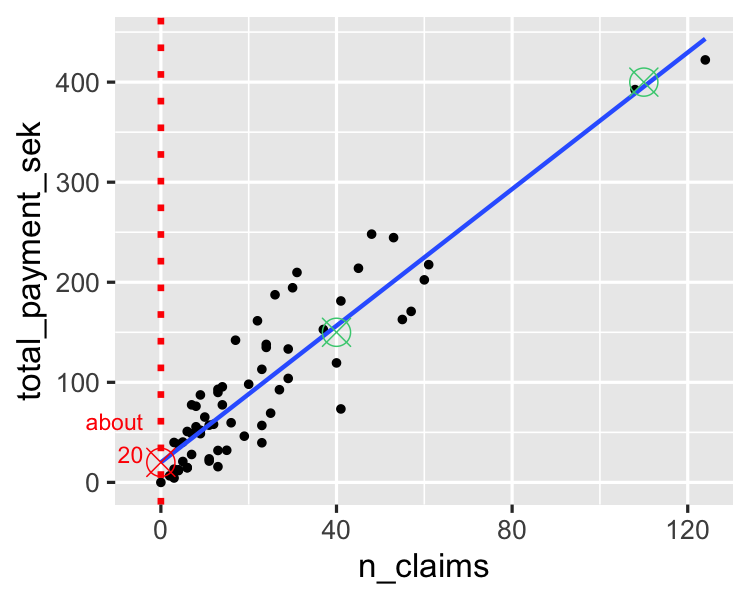
Le diagramme en nuage de points représentant le paiement total par rapport au nombre de réclamations, annoté de deux points sur la courbe de tendance. Un point correspond à 1 500 couronnes et 40 réclamations ; un autre point correspond à 3 500 couronnes et 100 réclamations.

Introduction à la régression avec statsmodels en Python

Évaluation de la pente

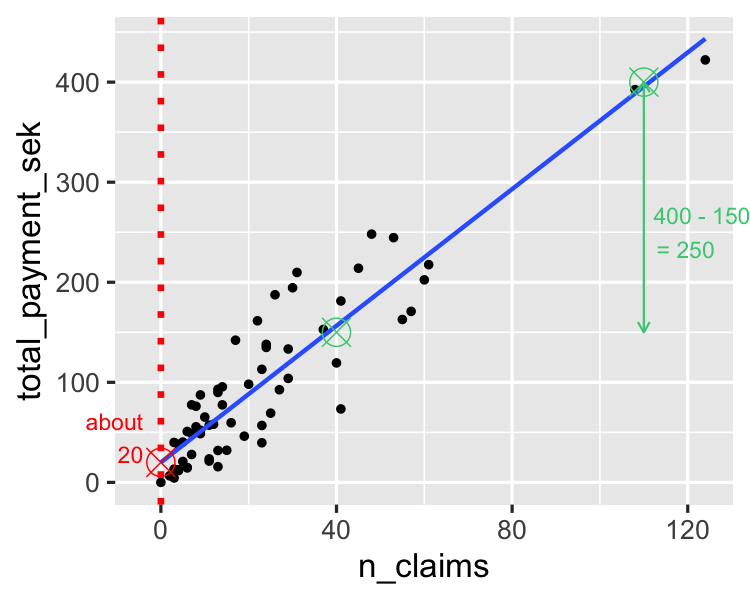
Le diagramme en nuage de points du paiement total par rapport au nombre de réclamations, annoté avec la différence de paiement entre les deux points. 3 500 couronnes moins 1 500 couronnes font 2 000 couronnes.

Introduction à la régression avec statsmodels en Python

Évaluation de la pente

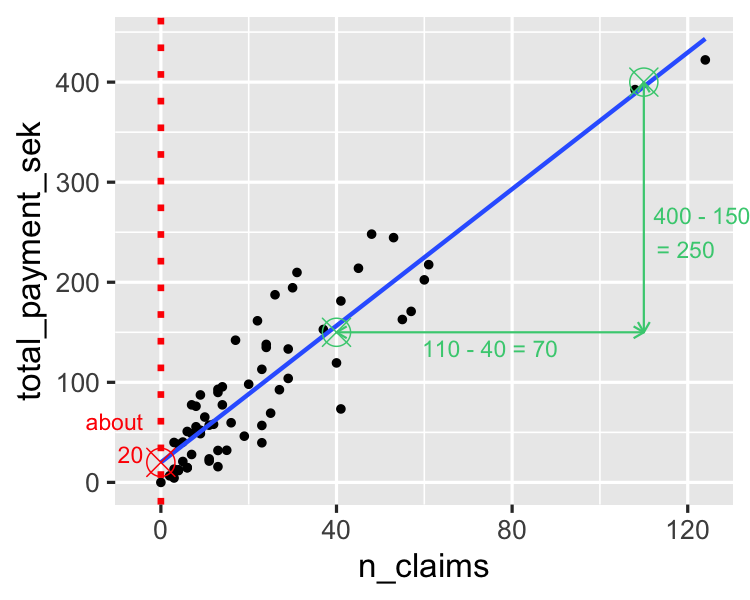
Le diagramme en nuage de points représentant le paiement total par rapport au nombre de réclamations, annoté avec la différence entre le nombre de réclamations pour les deux points. 100 réclamations moins 40 réclamations équivaut à 60 réclamations.

Introduction à la régression avec statsmodels en Python

Évaluation de la pente

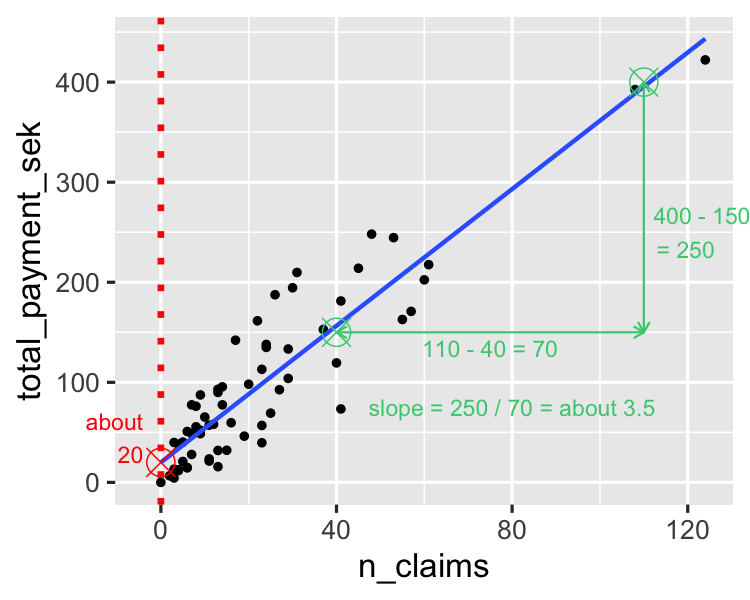
Le diagramme en nuage de points du paiement total par rapport au nombre de réclamations, annoté avec le ratio de la différence et du paiement ainsi que la différence dans le nombre de réclamations. 2 000 divisé par 60 donne environ 33.

Introduction à la régression avec statsmodels en Python

Exécution d'un modèle

from statsmodels.formula.api import ols

mdl_payment_vs_claims = ols("total_payment_sek ~ n_claims",
                            data=swedish_motor_insurance)


mdl_payment_vs_claims = mdl_payment_vs_claims.fit()

print(mdl_payment_vs_claims.params)

Intercept    19.994486
n_claims      3.413824
dtype: float64
Introduction à la régression avec statsmodels en Python

Interprétation des coefficients du modèle

Intercept    19.994486
n_claims      3.413824
dtype: float64

Équation

$\text{total\_payment\_sek} = 19.99 + 3.41 * \text{n\_claims}$

Introduction à la régression avec statsmodels en Python

Passons à la pratique !

Introduction à la régression avec statsmodels en Python

Preparing Video For Download...