Variables explicatives catégorielles

Introduction à la régression avec statsmodels en Python

Maarten Van den Broeck

Content Developer at DataCamp

Ensemble de données sur les poissons

  • Chaque ligne représente un poisson.
  • L’ensemble de données contient 128 lignes.
  • Il existe quatre espèces de poissons :
    • Brème commune
    • Perche européenne
    • Grand brochet
    • Gardon
species mass_g
Brème commune 242,0
Perche 5,9
Brochet 200,0
Gardon 40,0
... ...
Introduction à la régression avec statsmodels en Python

Visualisation variable numérique / catégorielle

import matplotlib.pyplot as plt
import seaborn as sns

sns.displot(data=fish,
            x="mass_g",
            col="species",
            col_wrap=2,
            bins=9)

plt.show()

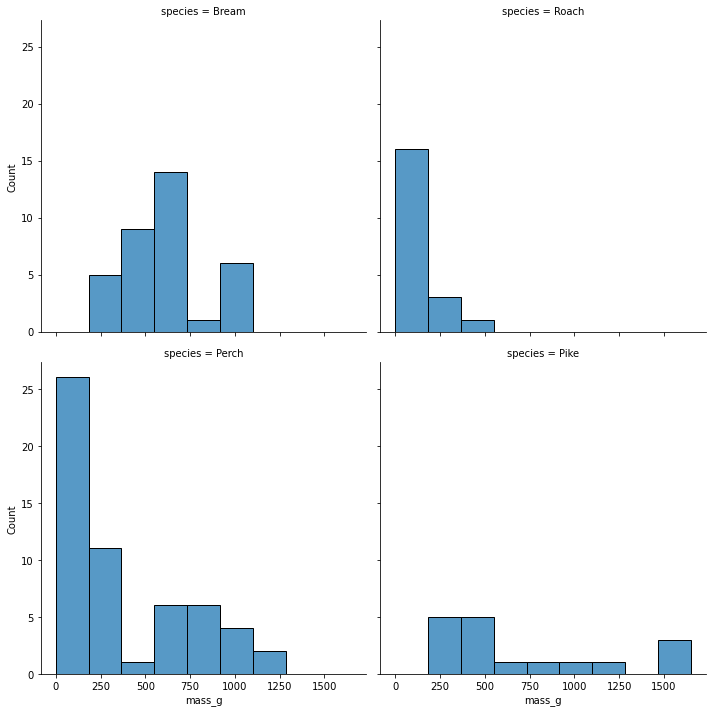
Histogramme à facettes représentant le nombre de poissons en fonction de leur poids. Chaque panneau contient une espèce : brème commune, perche, brochet ou gardon.

Introduction à la régression avec statsmodels en Python

Statistiques sommaires : masse moyenne selon les espèces

summary_stats = fish.groupby("species")["mass_g"].mean()
print(summary_stats)

species
Bream    617.828571
Perch    382.239286
Pike     718.705882
Roach    152.050000
Name: mass_g, dtype: float64
Introduction à la régression avec statsmodels en Python

Régression linéaire

from statsmodels.formula.api import ols 
mdl_mass_vs_species = ols("mass_g ~ species", data=fish).fit()

print(mdl_mass_vs_species.params)

Intercept           617.828571
species[T.Perch]   -235.589286
species[T.Pike]     100.877311
species[T.Roach]   -465.778571
Introduction à la régression avec statsmodels en Python

Modèle avec ou sans ordonnée à l’origine

À partir de la diapositive précédente, modèle avec ordonnée à l’origine

mdl_mass_vs_species = ols(
  "mass_g ~ species", data=fish).fit()

print(mdl_mass_vs_species.params)

Intercept           617.828571
species[T.Perch]   -235.589286
species[T.Pike]     100.877311
species[T.Roach]   -465.778571

Les coefficients sont relatifs à l'ordonnée à l'origine : $617.83 - 235.59 = 382.24!$

Modèle sans ordonnée à l’origine

mdl_mass_vs_species = ols(
  "mass_g ~ species + 0", data=fish).fit()

print(mdl_mass_vs_species.params)

species[Bream]    617.828571
species[Perch]    382.239286
species[Pike]     718.705882
species[Roach]    152.050000

Dans le cas d'une variable catégorielle unique, les coefficients représentent les moyennes.

Introduction à la régression avec statsmodels en Python

Passons à la pratique !

Introduction à la régression avec statsmodels en Python

Preparing Video For Download...