Visualisation de l'ajustement du modèle
Introduction à la régression avec statsmodels en Python

Maarten Van den Broeck
Content Developer at DataCamp
Propriétés résiduelles d'un ajustement satisfaisant
- Les résidus sont normalement distribués.
- La moyenne des résidus est égale à zéro.
Brème commune et perche à nouveau
Brème commune : le modèle « exemplaire »
mdl_bream = ols("mass_g ~ length_cm", data=bream).fit()
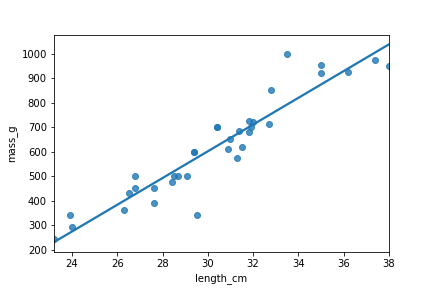
Perche : le modèle « inapproprié »
mdl_perch = ols("mass_g ~ length_cm", data=perch).fit()
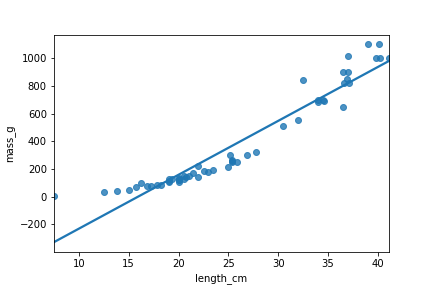
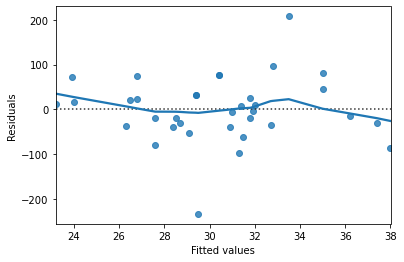
Résidus vs ajustés
Brème commune
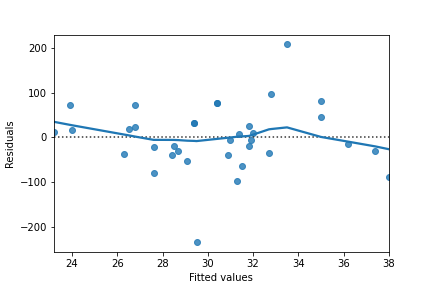
Perche
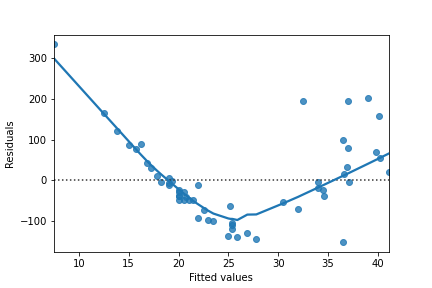
Graphique Q-Q
Brème commune
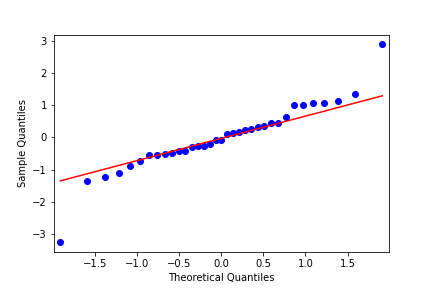
Perche
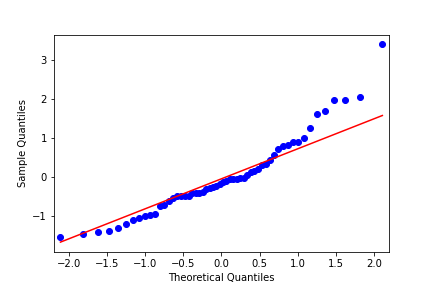
Graphique d'emplacement à l'échelle
Brème commune
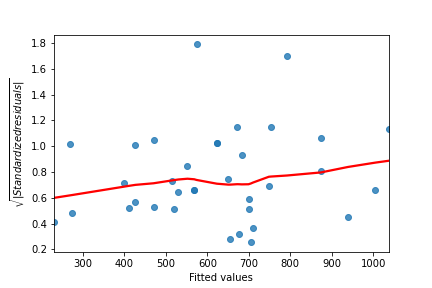
Perche
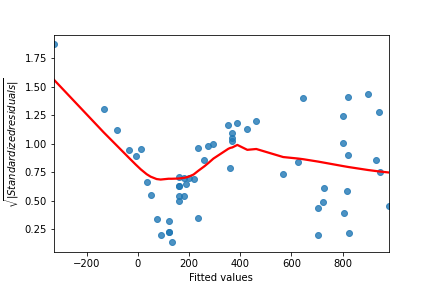
residplot()
sns.residplot(x="length_cm", y="mass_g", data=bream, lowess=True)
plt.xlabel("Fitted values")
plt.ylabel("Residuals")
qqplot()
from statsmodels.api import qqplot
qqplot(data=mdl_bream.resid, fit=True, line="45")

Graphique d'emplacement à l'échelle
model_norm_residuals_bream = mdl_bream.get_influence().resid_studentized_internalmodel_norm_residuals_abs_sqrt_bream = np.sqrt(np.abs(model_norm_residuals_bream))sns.regplot(x=mdl_bream.fittedvalues, y=model_norm_residuals_abs_sqrt_bream, ci=None, lowess=True)plt.xlabel("Fitted values") plt.ylabel("Sqrt of abs val of stdized residuals")
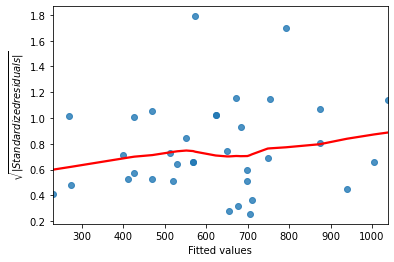
Passons à la pratique !
Introduction à la régression avec statsmodels en Python

