Prévisions et rapports de cotes

Introduction à la régression avec statsmodels en Python

Maarten Van den Broeck

Content Developer at DataCamp

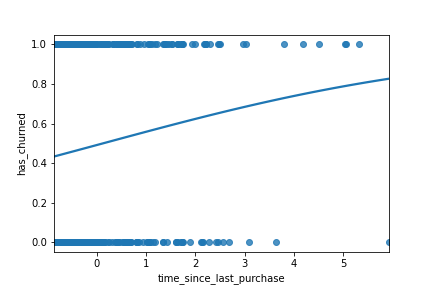
Les prédictions de la fonction regplot()

sns.regplot(x="time_since_last_purchase",
            y="has_churned",
            data=churn,
            ci=None,
            logistic=True)

plt.show()

Diagramme en nuage de points représentant l’attrition en fonction du temps écoulé depuis le dernier achat, avec une courbe de tendance logistique.

Introduction à la régression avec statsmodels en Python

Faire des prévisions

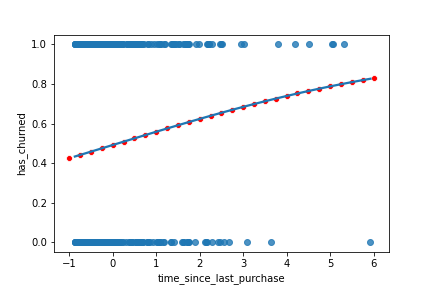
mdl_recency = logit("has_churned ~ time_since_last_purchase",
                    data = churn).fit()


explanatory_data = pd.DataFrame(
  {"time_since_last_purchase": np.arange(-1, 6.25, 0.25)})


prediction_data = explanatory_data.assign(
    has_churned = mdl_recency.predict(explanatory_data))
Introduction à la régression avec statsmodels en Python

Ajout de prévisions de points

sns.regplot(x="time_since_last_purchase",
            y="has_churned",
            data=churn,
            ci=None,
            logistic=True)

sns.scatterplot(x="time_since_last_purchase",
                y="has_churned",
                data=prediction_data,
                color="red")

plt.show()

Le diagramme en nuage de points représentant l’attrition en fonction du temps écoulé depuis le dernier achat, avec une courbe de tendance logistique. Le graphique est annoté avec les résultats de predict(), qui suivent exactement la courbe de tendance.

Introduction à la régression avec statsmodels en Python

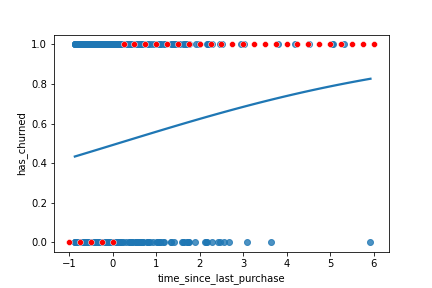
Obtenir le résultat le plus probable

prediction_data = explanatory_data.assign(
    has_churned = mdl_recency.predict(explanatory_data))

prediction_data["most_likely_outcome"] = np.round(prediction_data["has_churned"])
Introduction à la régression avec statsmodels en Python

Visualisation du résultat le plus probable

sns.regplot(x="time_since_last_purchase",
            y="has_churned",
            data=churn,
            ci=None,
            logistic=True)

sns.scatterplot(x="time_since_last_purchase",
                y="most_likely_outcome",
                data=prediction_data,
                color="red")

plt.show()

Le diagramme en nuage de points représentant l’attrition en fonction du temps écoulé depuis le dernier achat, avec une courbe de tendance logistique. Le graphique est annoté avec les résultats les plus probables. Si peu de temps s'est écoulé depuis le dernier achat, le résultat le plus probable est l'absence d’attrition. Si le dernier achat remonte à longtemps, le résultat le plus probable est l’attrition.

Introduction à la régression avec statsmodels en Python

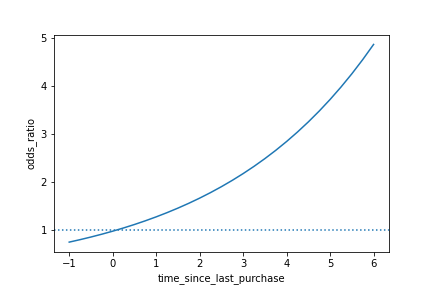
Rapports de cotes

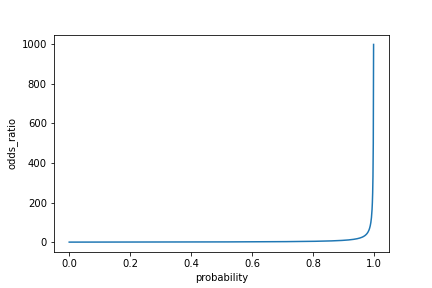
Le rapport de cotes est la probabilité qu'un événement se produise divisée par la probabilité qu'il ne se produise pas.

$$ \text{odds\_ratio} = \frac{\text{probability}}{(1 - \text{probability)}} $$

$$ \text{odds\_ratio} = \frac{0.25}{(1 - 0.25)} = \frac{1}{3} $$

Graphique linéaire représentant le rapport de cotes par rapport à la probabilité. La courbe augmente de manière asymptotique vers l'infini à mesure que la probabilité tend vers un.

Introduction à la régression avec statsmodels en Python

Calcul du rapport de cotes

prediction_data["odds_ratio"] = prediction_data["has_churned"] / 
                                (1 - prediction_data["has_churned"])
Introduction à la régression avec statsmodels en Python

Visualisation du rapport de cotes

sns.lineplot(x="time_since_last_purchase",
             y="odds_ratio",
             data=prediction_data)


plt.axhline(y=1,
            linestyle="dotted")


plt.show()

Graphique linéaire représentant le rapport de cotes en fonction du temps écoulé depuis le dernier achat, avec une ligne correspondant à un rapport de cotes égal à un. Si peu de temps s'est écoulé depuis le dernier achat, le résultat le plus probable est l'absence d’attrition. Les risques d’attrition augmentent à mesure que le temps écoulé depuis le dernier achat s'allonge, jusqu'à atteindre cinq fois les chances de fidélisation.

Introduction à la régression avec statsmodels en Python

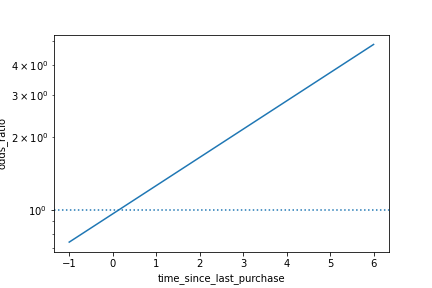
Visualisation du rapport de cotes logarithmique

sns.lineplot(x="time_since_last_purchase",
             y="odds_ratio",
             data=prediction_data)

plt.axhline(y=1,
            linestyle="dotted")

plt.yscale("log")

plt.show()

Le graphique linéaire représentant le rapport de cotes en fonction du temps écoulé depuis le dernier achat, avec une ligne correspondant à un rapport de cotes égal à un. L'axe des y utilise une échelle logarithmique, ce qui a pour conséquence de rendre la courbe du rapport de cotes linéaire.

Introduction à la régression avec statsmodels en Python

Calcul du rapport de cotes logarithmique

prediction_data["log_odds_ratio"] = np.log(prediction_data["odds_ratio"])
Introduction à la régression avec statsmodels en Python

Toutes les prévisions réunies

time_since_last_prchs has_churned most_likely_rspns odds_ratio log_odds_ratio
0 0,491 0 0,966 -0,035
2 0,623 1 1,654 0,503
4 0,739 1 2,834 1,042
6 0,829 1 4,856 1,580
... ... ... ... ...
Introduction à la régression avec statsmodels en Python

Comparaison des échelles

Faire évoluer Les valeurs sont-elles faciles à interpréter ? Les modifications sont-elles faciles à interpréter ? Est-ce exact ?
Probabilité ✔ ✘ ✔
Résultat le plus probable ✔✔ ✔ ✘
Rapport de cotes ✔ ✘ ✔
Rapport de cotes logarithmique ✘ ✔ ✔
Introduction à la régression avec statsmodels en Python

Passons à la pratique !

Introduction à la régression avec statsmodels en Python

Preparing Video For Download...