Corrélation
Introduction aux statistiques

George Boorman
Curriculum Manager, DataCamp
Relations entre deux variables
Coefficient de corrélation de Pearson
- Publié par Karl Pearson en 1896.
- Mesure la force d'une relation entre deux variables
- Nombre compris entre moins un et un
- La valeur absolue correspond à la force de la relation
- Le signe (+ ou -) correspond au sens de la relation
1 https://royalsocietypublishing.org/doi/10.1098/rsta.1896.0007
Relations linéaires
- Linéaire = changements proportionnels entre les variables dépendantes et indépendantes
Valeurs = solidité de la relation
0,99 (relation très forte)
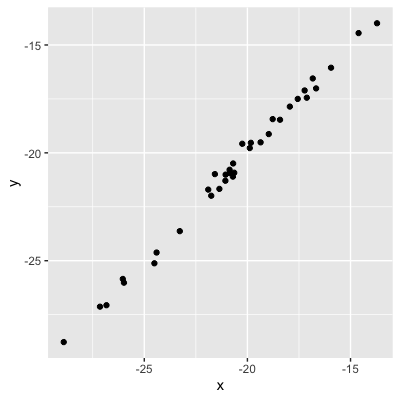
Valeurs = solidité de la relation
0,99 (relation très forte)

0,75 (relation forte)
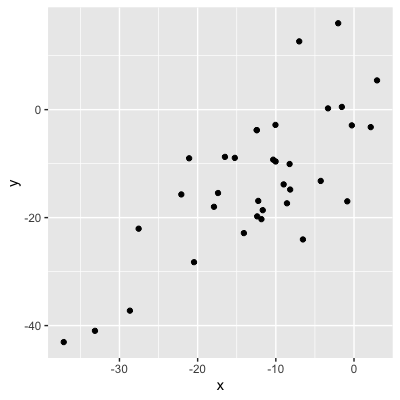
Valeurs = solidité de la relation
0,56 (relation modérée)
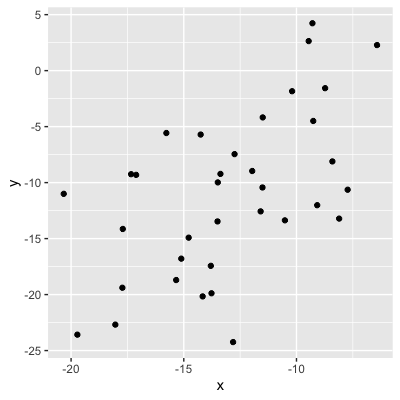
Valeurs = solidité de la relation
0,56 (relation modérée)

0,21 (relation faible)
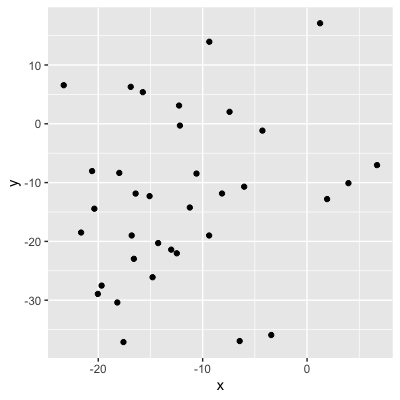
Valeurs = solidité de la relation
0,04 (pas de relation)
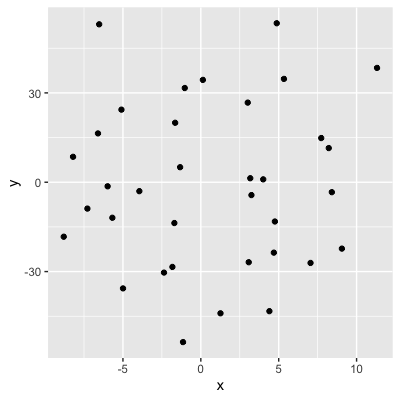
- Connaître la valeur de x ne nous fournit aucune information sur y
Signe = direction
0,75 : lorsque x augmente, y augmente

-0,75 : lorsque x augmente, y diminue
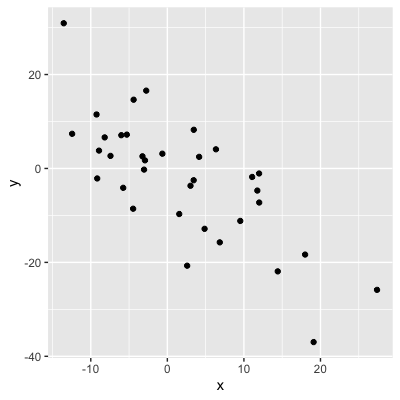
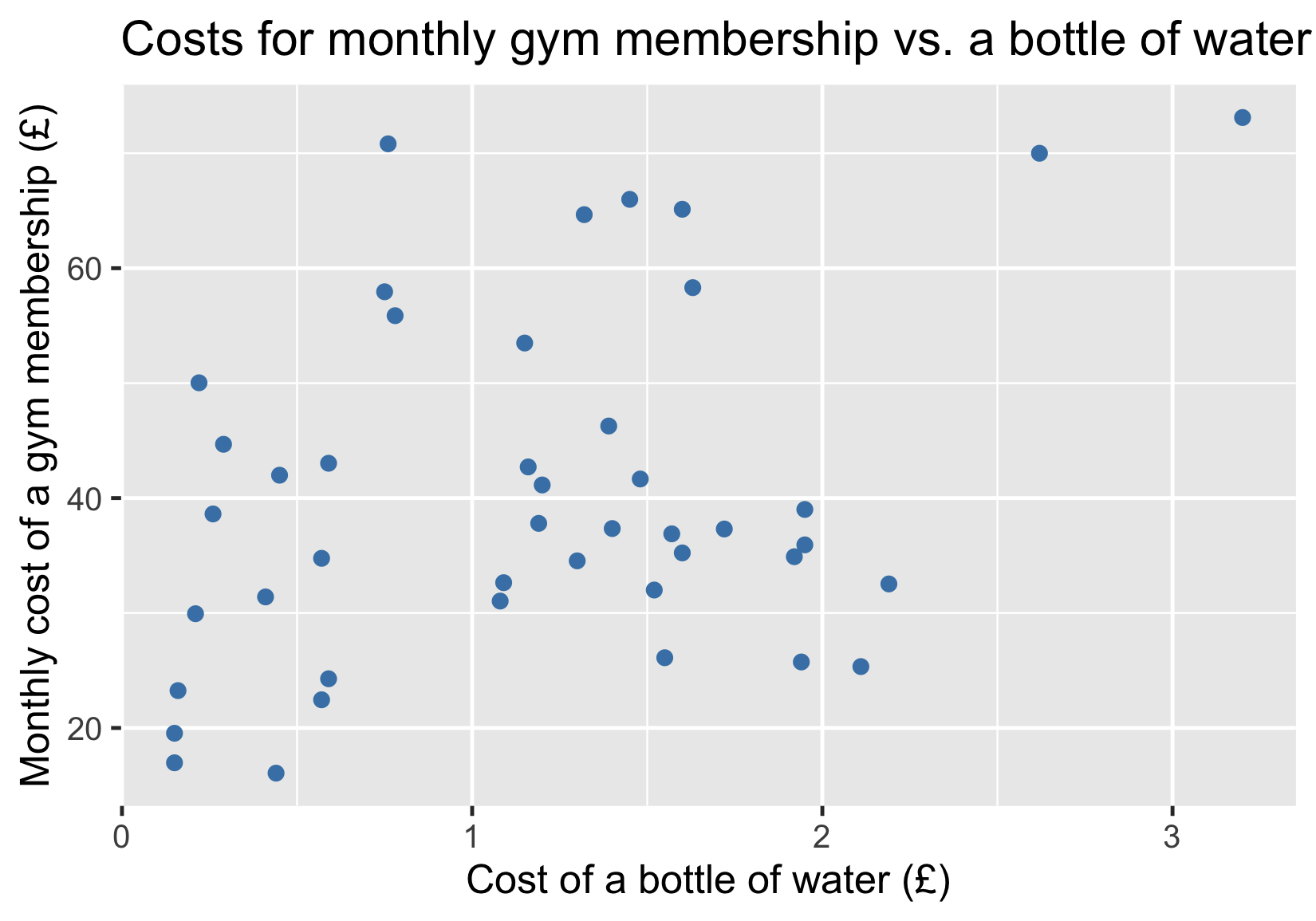
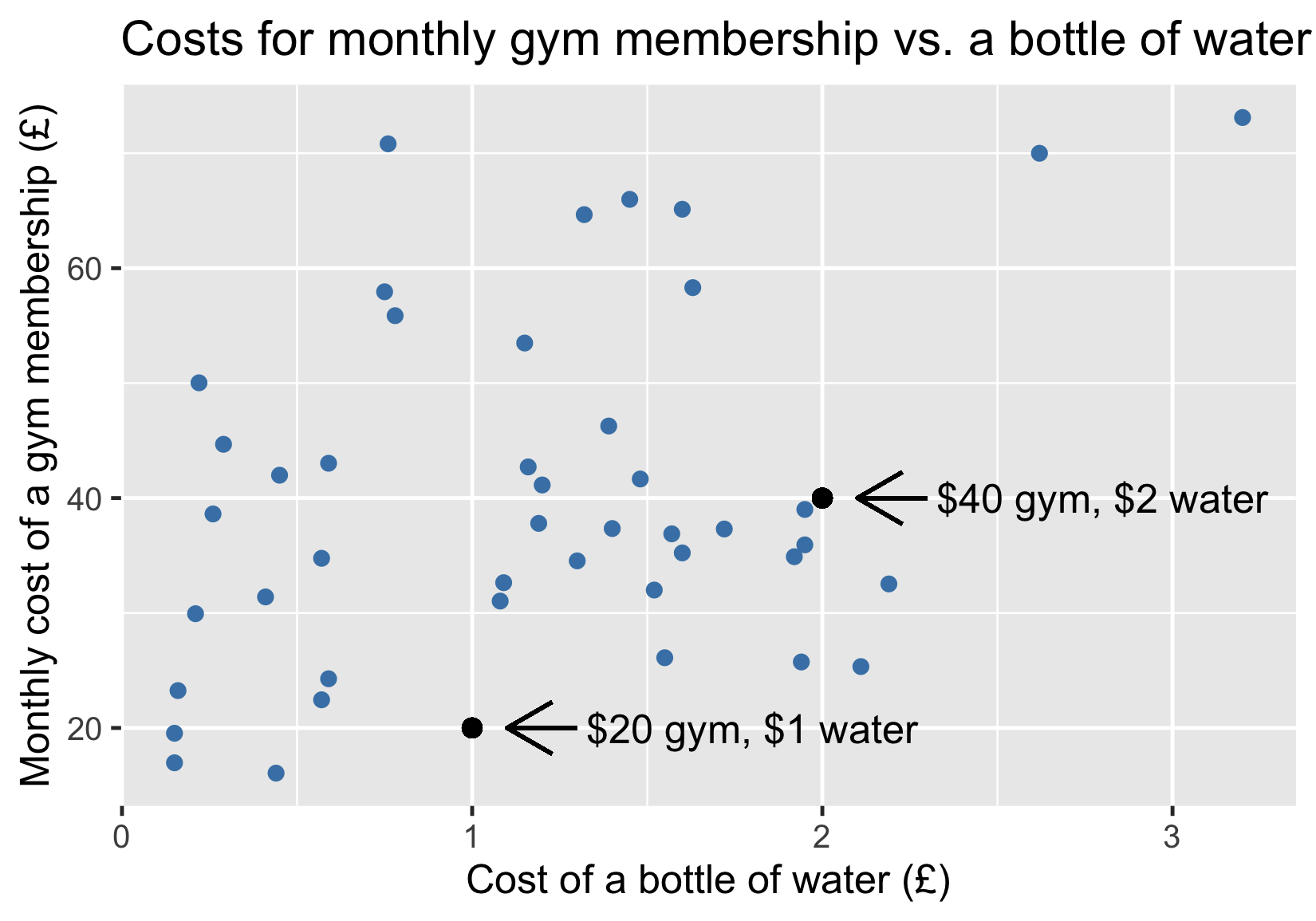
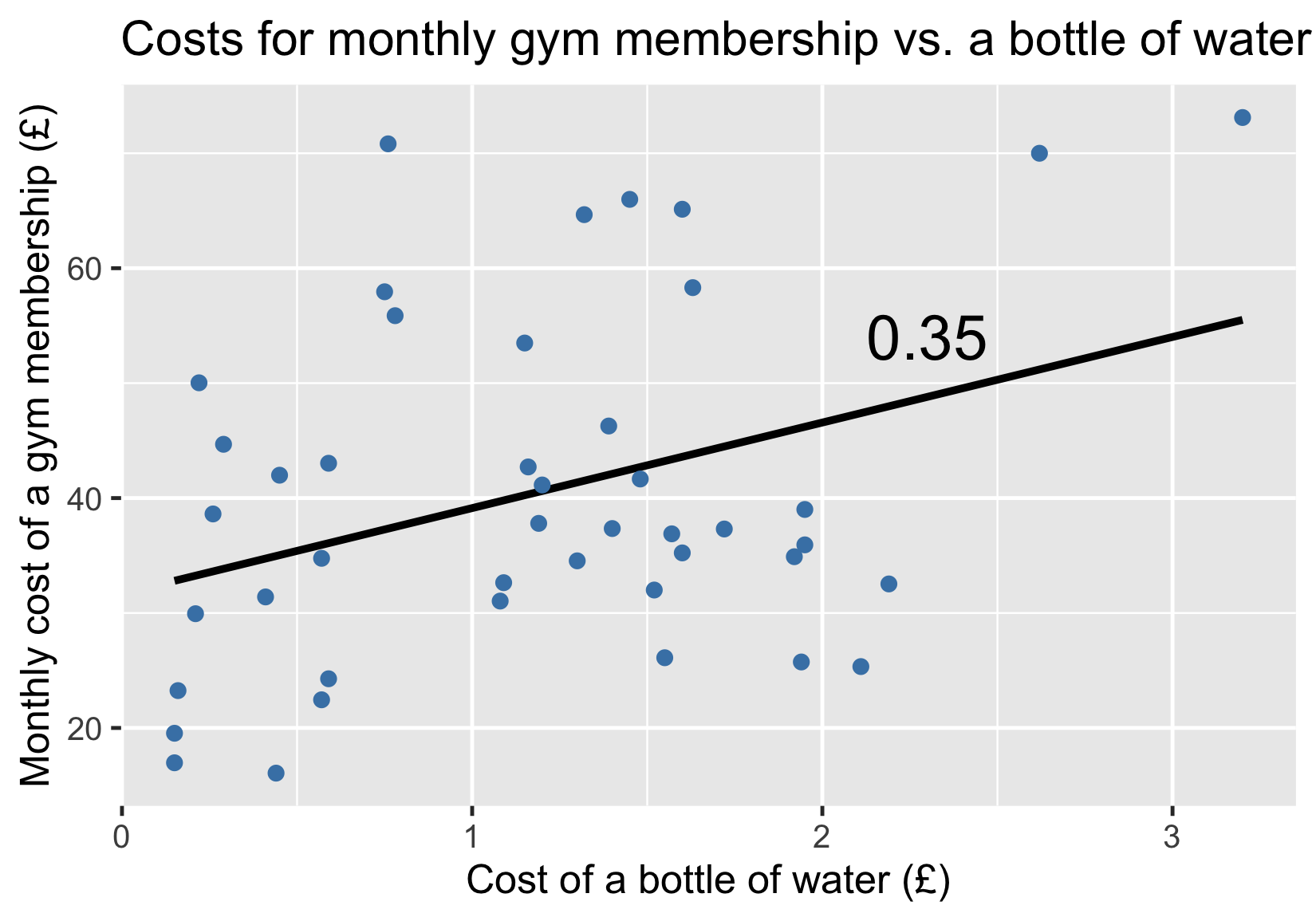
Coûts de la salle de sport vs coûts de l'eau

Ajout d’une ligne de tendance
Espérance de vie vs coût d'une bouteille d'eau
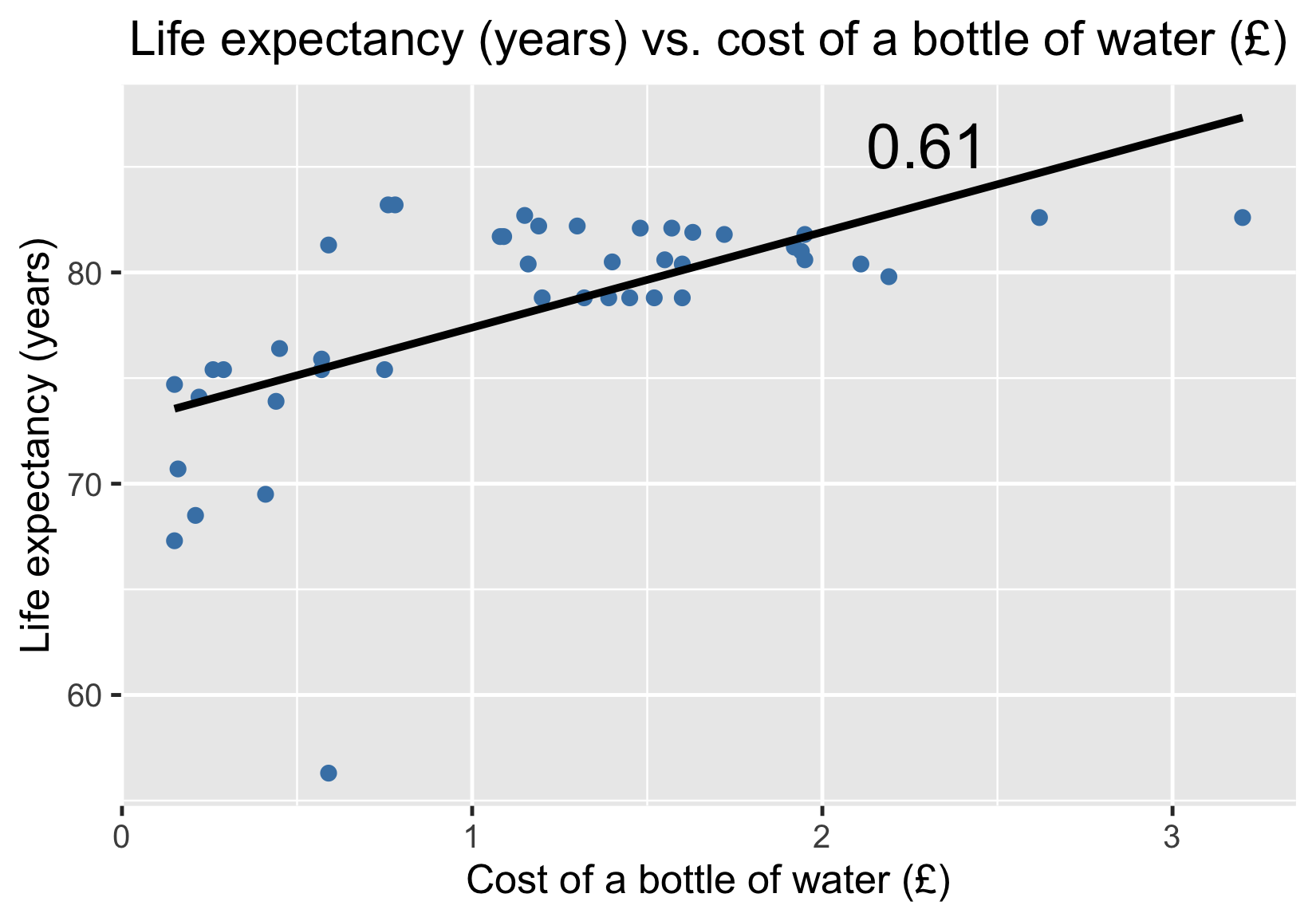
Corrélation ≠ relation de cause à effet
- L'augmentation du coût de l'eau entraînera-t-elle une augmentation de l'espérance de vie ?


- Corrélation ≠ relation de cause à effet
1 Crédit d'image : https://unsplash.com/@micheile; https://unsplash.com/@jon_chng
Variables confusionnelles
Quels autres facteurs pourraient influencer l'espérance de vie ?
- Une bouteille d'eau coûte plus cher dans les pays à économie forte
- Ces pays offrent généralement un accès à des soins de santé de haute qualité
La vigueur de l'économie pourrait constituer une variable confusionnelle
- Une variable confusionnelle n'est pas mesurée, mais peut influencer la relation entre nos variables

Passons à la pratique !
Introduction aux statistiques

