La distribution binomiale
Introduction aux statistiques

George Boorman
Curriculum Manager, DataCamp
Jeu de pile ou face
Résultats binaires
Lancer une seule pièce, plusieurs fois
| Lancer de pièce | Résultat |
|---|---|
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 1 |
| 5 | 0 |
| 6 | 0 |
| 7 | 1 |
| 8 | 0 |
| 9 | 1 |
| 10 | 1 |
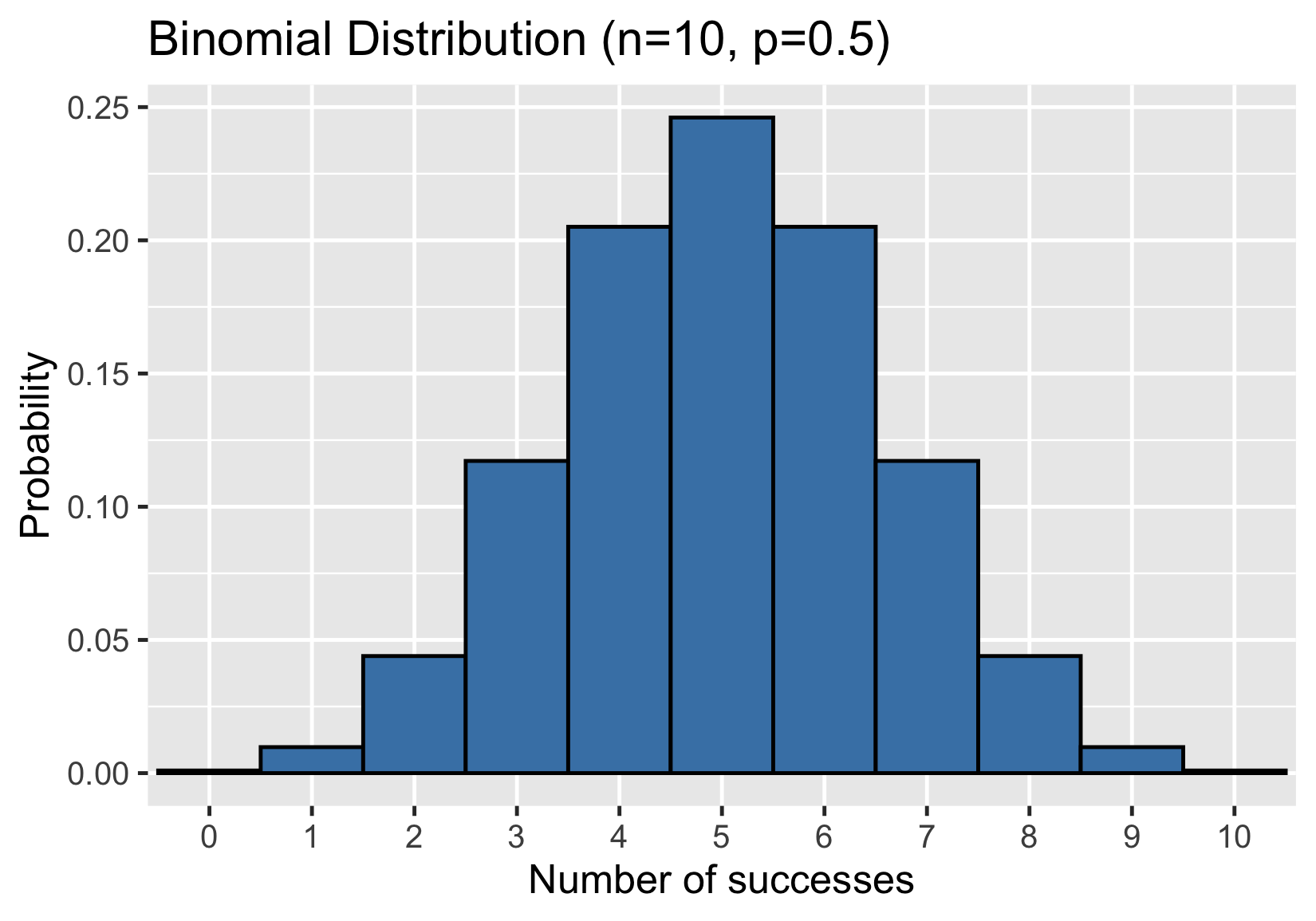
Distribution binomiale
Distribution de probabilité du nombre de réussites dans une séquence d’événements indépendants
Par exemple, le nombre de faces dans une séquence de lancers de pièce
Décrite par $n$ et $p$.
- $n$ : nombre total d'événements
- $p$ : probabilité de réussite
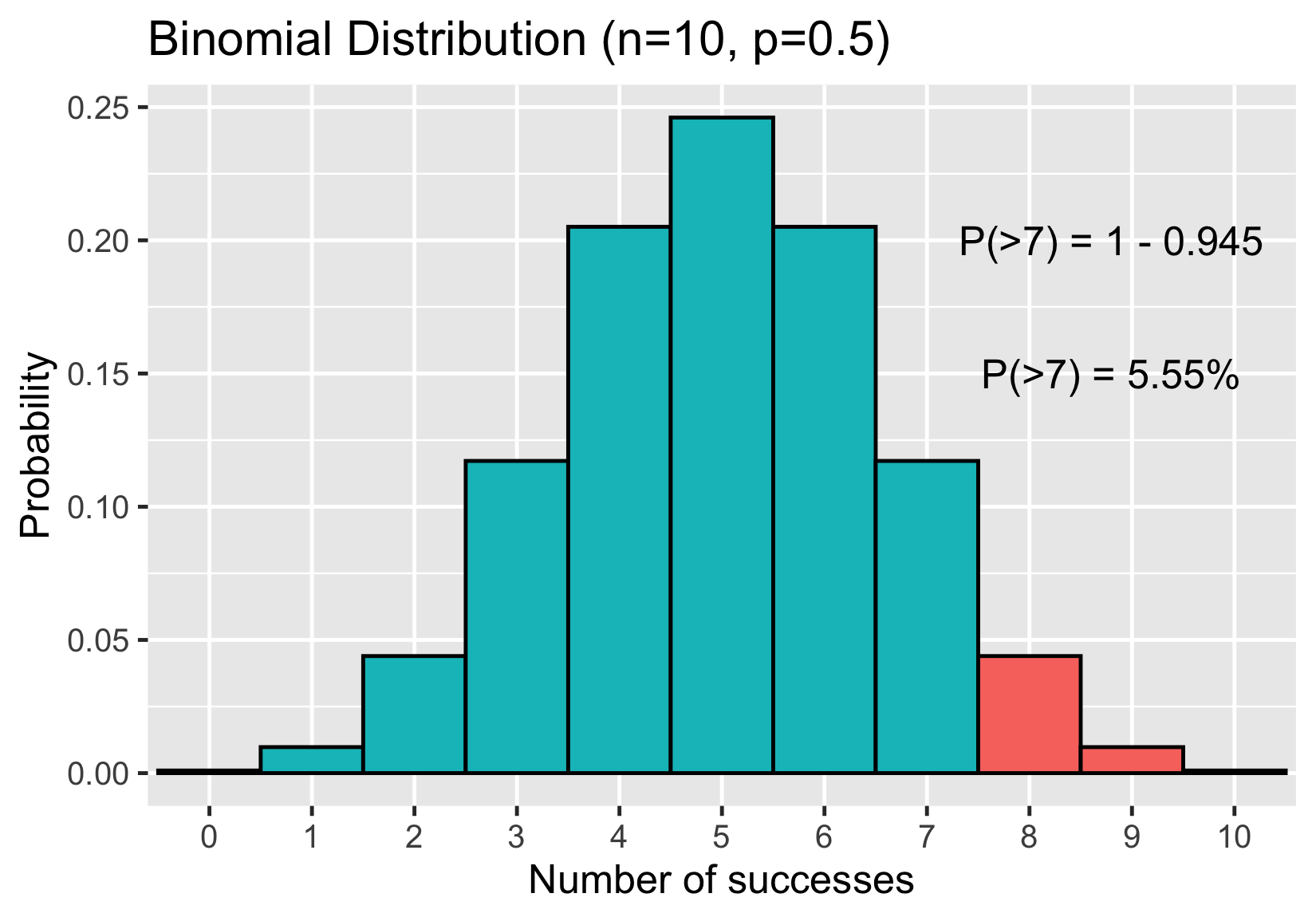
Distribution binomiale
Probabilité d'obtenir 7 faces ou moins
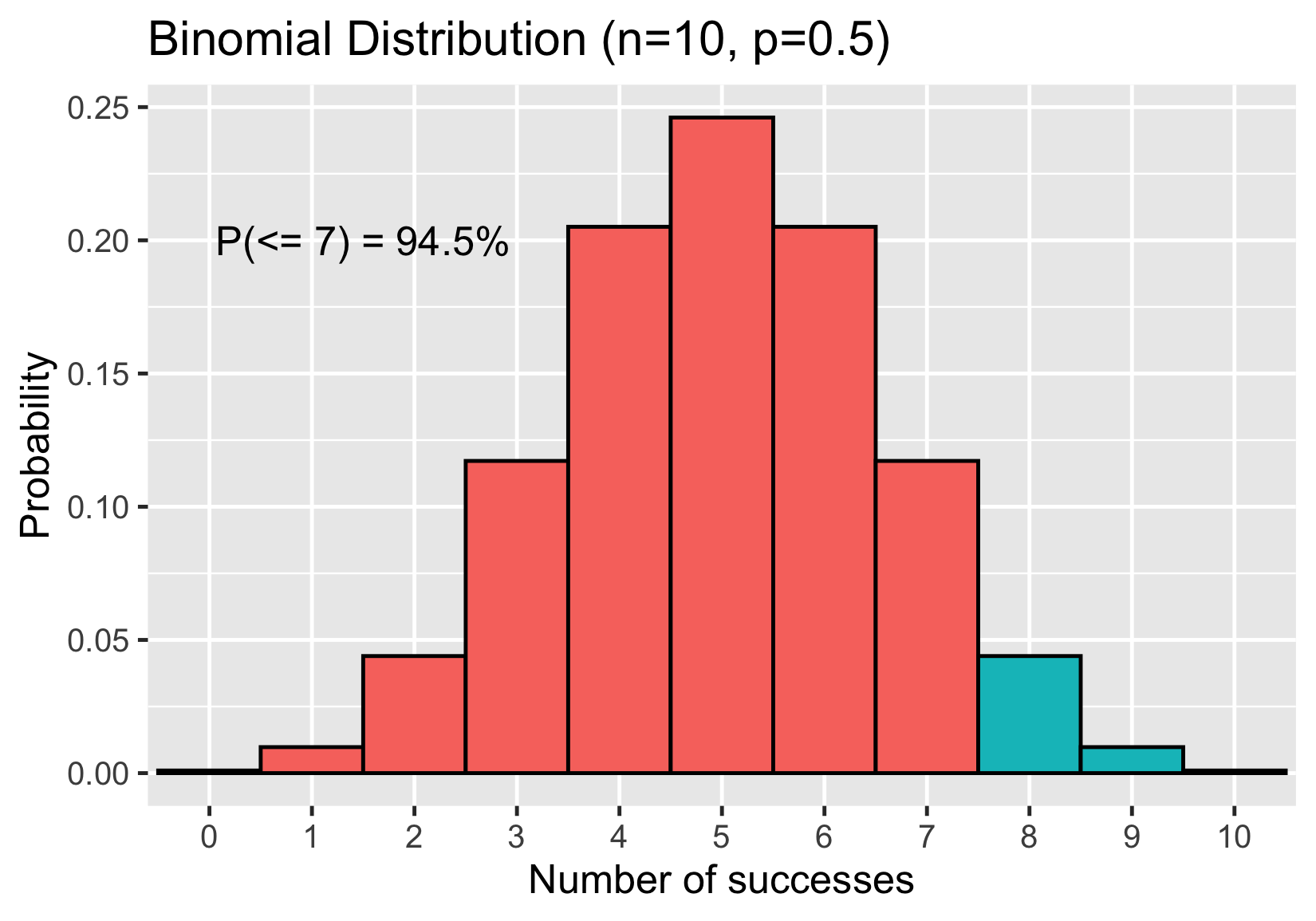
Probabilité d'obtenir 8 faces ou plus
Valeur attendue
${Expected \ value} = n \times p$
Nombre attendu de faces sur 10 lancers $= 10 \times 0,5 = 5$.
Si nous ne connaissons pas $p$, but know $n$ et la valeur attendue :
${p} = \frac{expected \ value}{n} $
Indépendance
La distribution binomiale est une distribution de probabilité du nombre de réussites dans une séquence d’événements indépendants
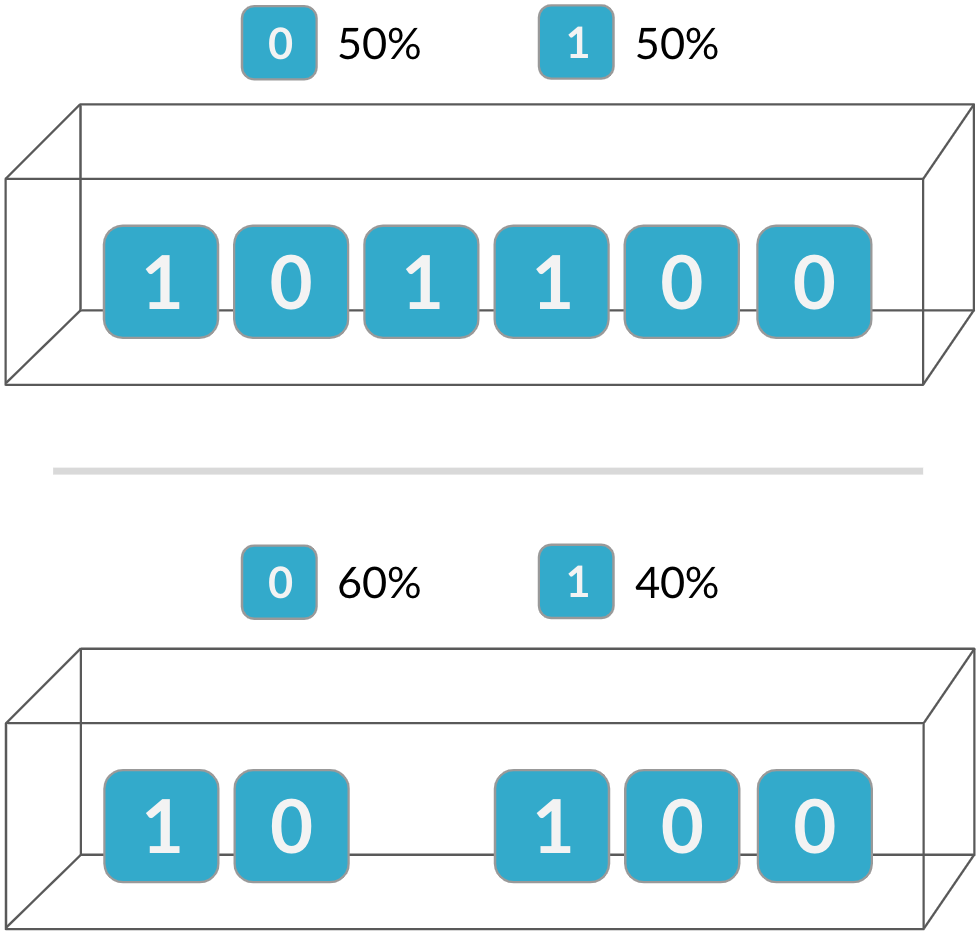
Indépendance
La distribution binomiale est une distribution de probabilité du nombre de réussites dans une séquence d’événements indépendants
Les probabilités du deuxième événement sont modifiées en raison du résultat du premier
Si les événements ne sont pas indépendants, la distribution binomiale ne s'applique pas !
Applications générales
La distribution binomiale peut être utilisée pour des événements indépendants produisant des résultats binaires
- Essai clinique visant à mesurer l'efficacité d'un médicament
- Efficace ou non
- Paris sur le résultat d'un match sportif
- Le parieur peut gagner ou perdre

Passons à la pratique !
Introduction aux statistiques

