Distributions discrètes
Introduction aux statistiques

George Boorman
Curriculum Manager, DataCamp

Les dés sont jetés
Choix des vendeurs

Distribution des probabilités
Décrit la probabilité de chaque résultat possible dans un scénario
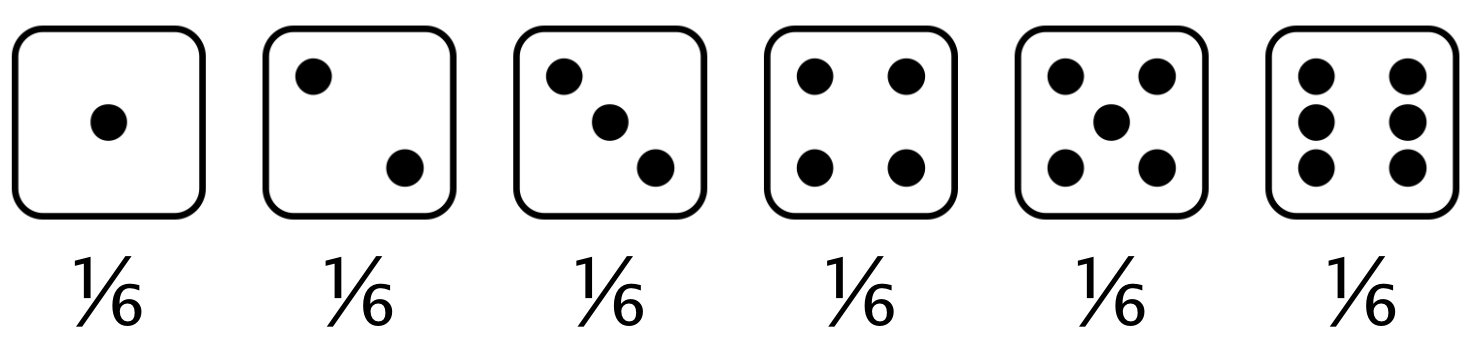
Valeur attendue : La moyenne d'une distribution des probabilités
Valeur attendue d’un lancer de dé équitable = $(1 \times \frac{1}{6}) + (2 \times \frac{1}{6}) +(3 \times \frac{1}{6}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3,5$.
Pourquoi les distributions de probabilité sont-elles importantes ?
- Nous aide à évaluer les risques et éclaire notre prise de décision
- Largement utilisée dans les tests d'hypothèses
- Probabilité que les résultats soient le fruit du hasard
Visualisation d’une distribution des probabilités
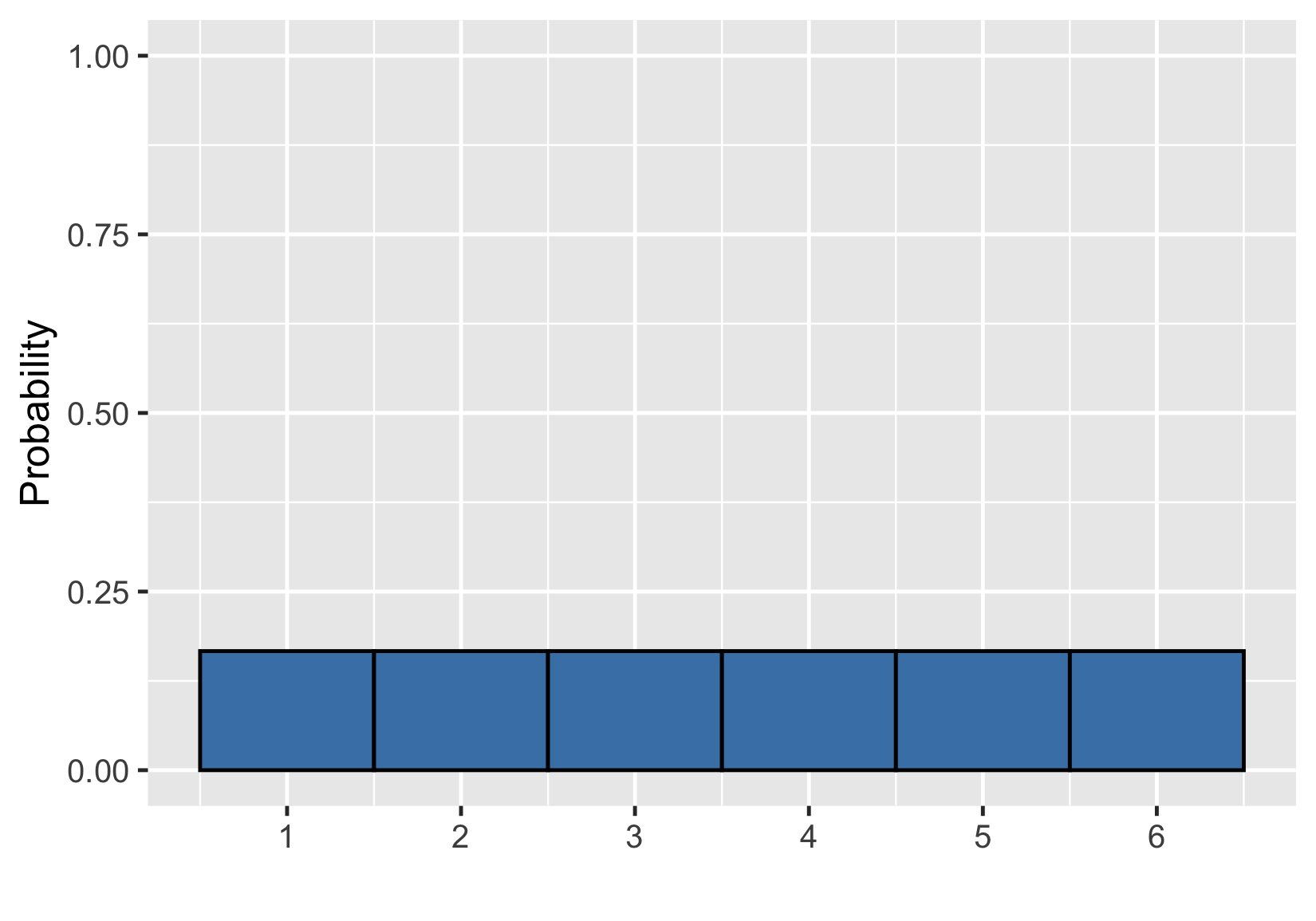
Probabilité = aire
$$P(\text{die roll}) \le 2 = ~?$$
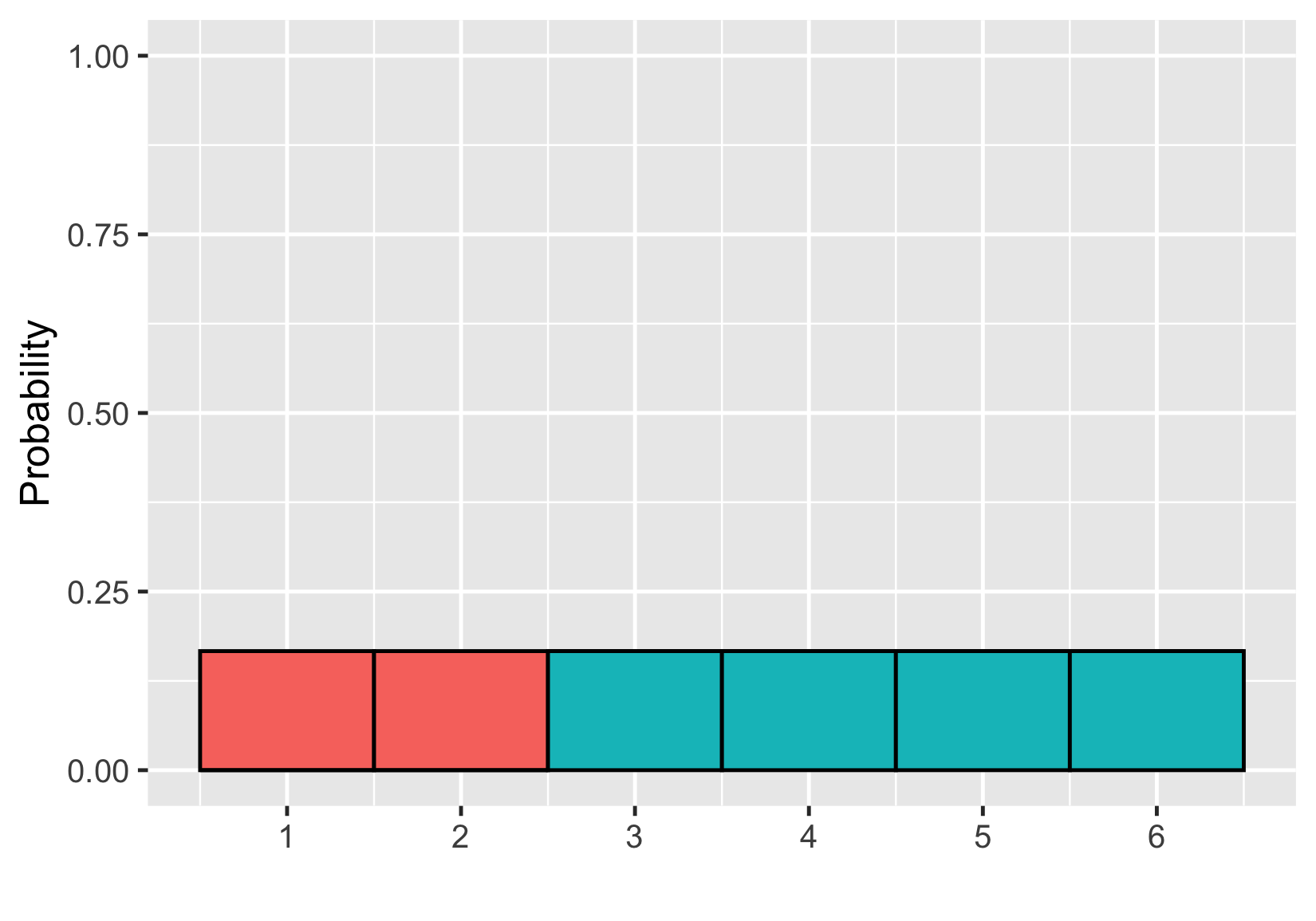
Probabilité = aire
$$P(\text{lancer de dé} \le 2) = 1/3$$
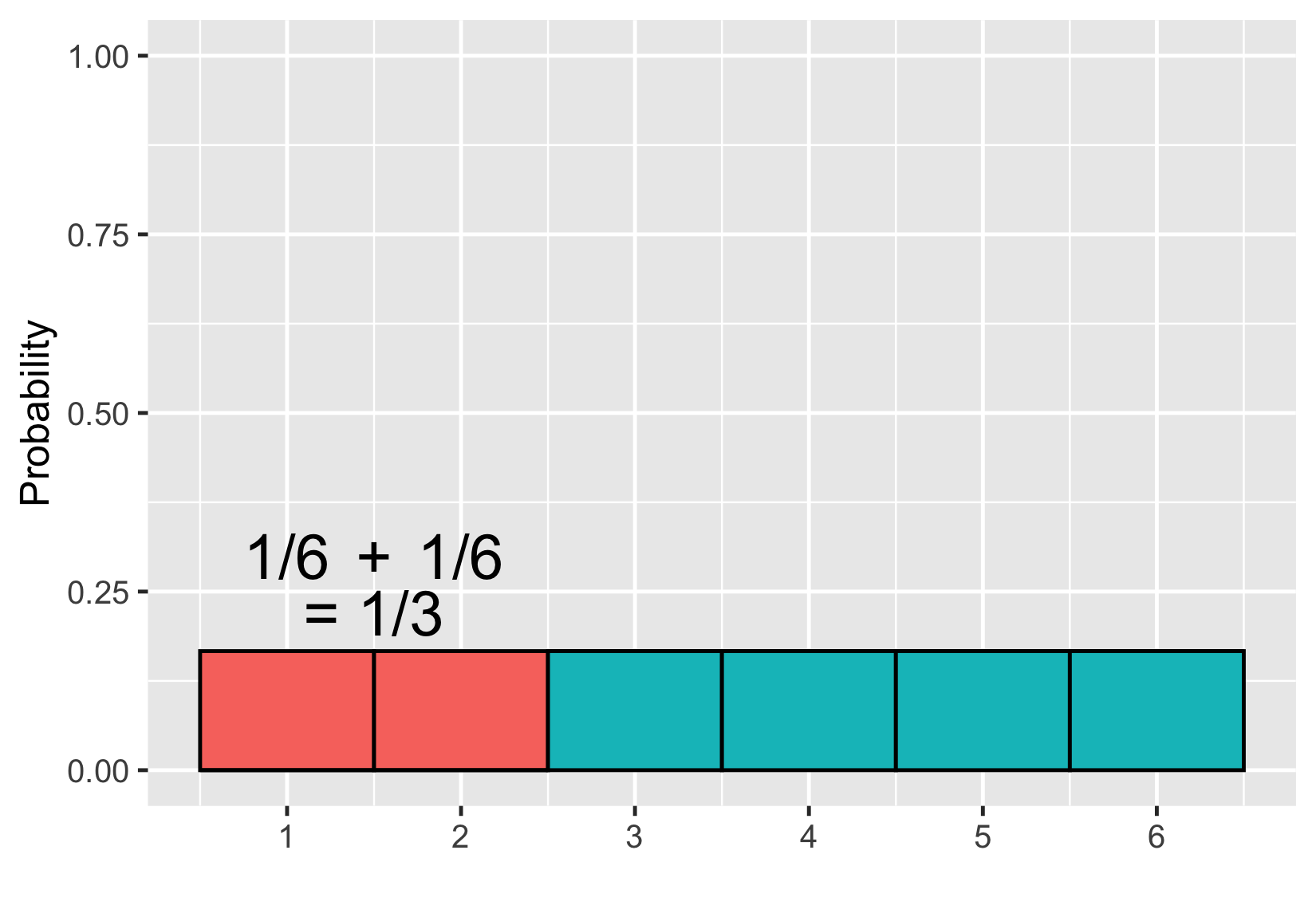
Dé irrégulier
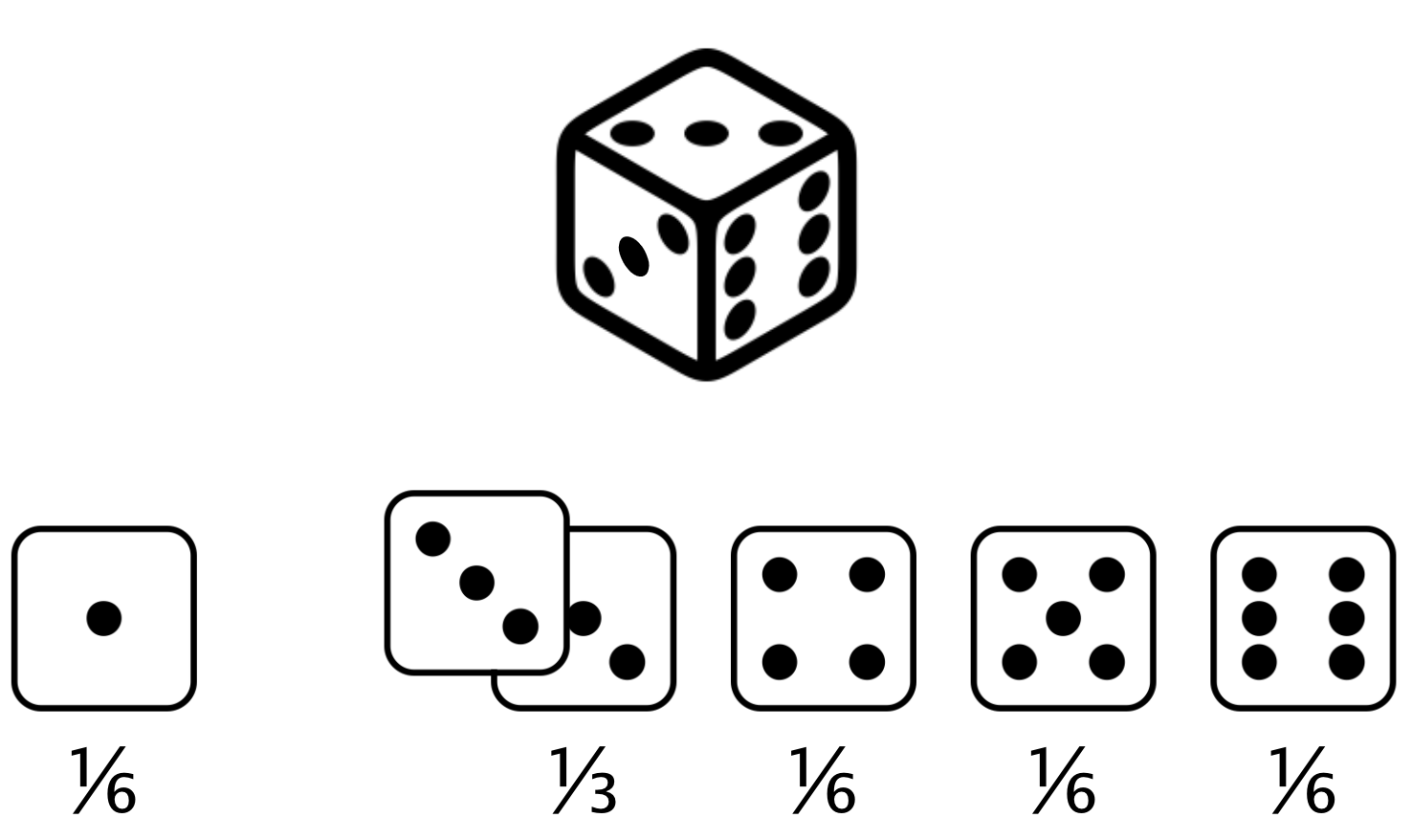
Valeur attendue d’un lancer de dé irrégulier = $(1 \times \frac{1}{6}) +(2 \times 0) +(3 \times \frac{1}{3}) +(4 \times \frac{1}{6}) +(5 \times \frac{1}{6}) +(6 \times \frac{1}{6}) = 3,67$
Visualiser des probabilités non uniformes
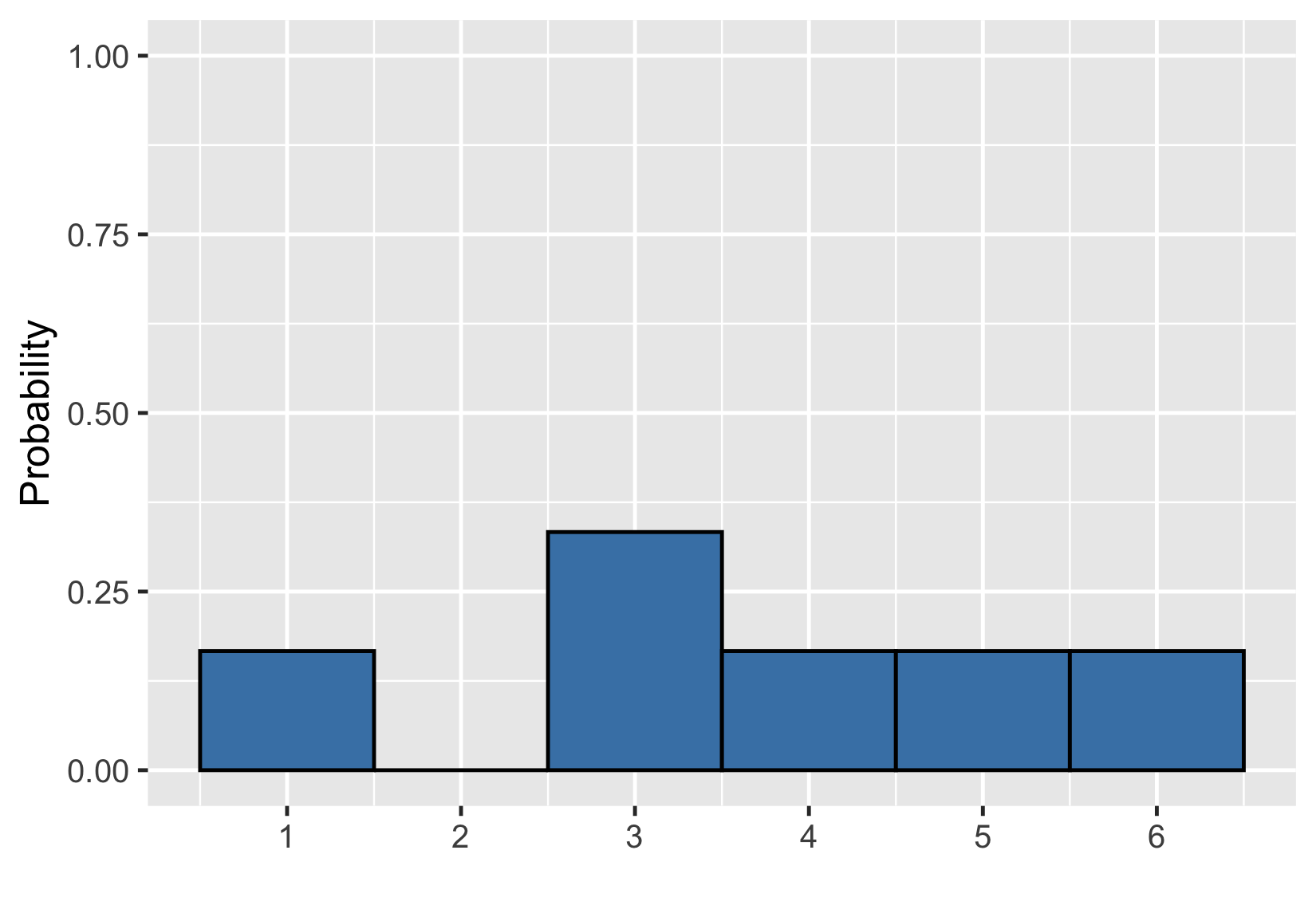
Addition d’aires
$$P(\text{uneven die roll}) \le 2 = ~?$$
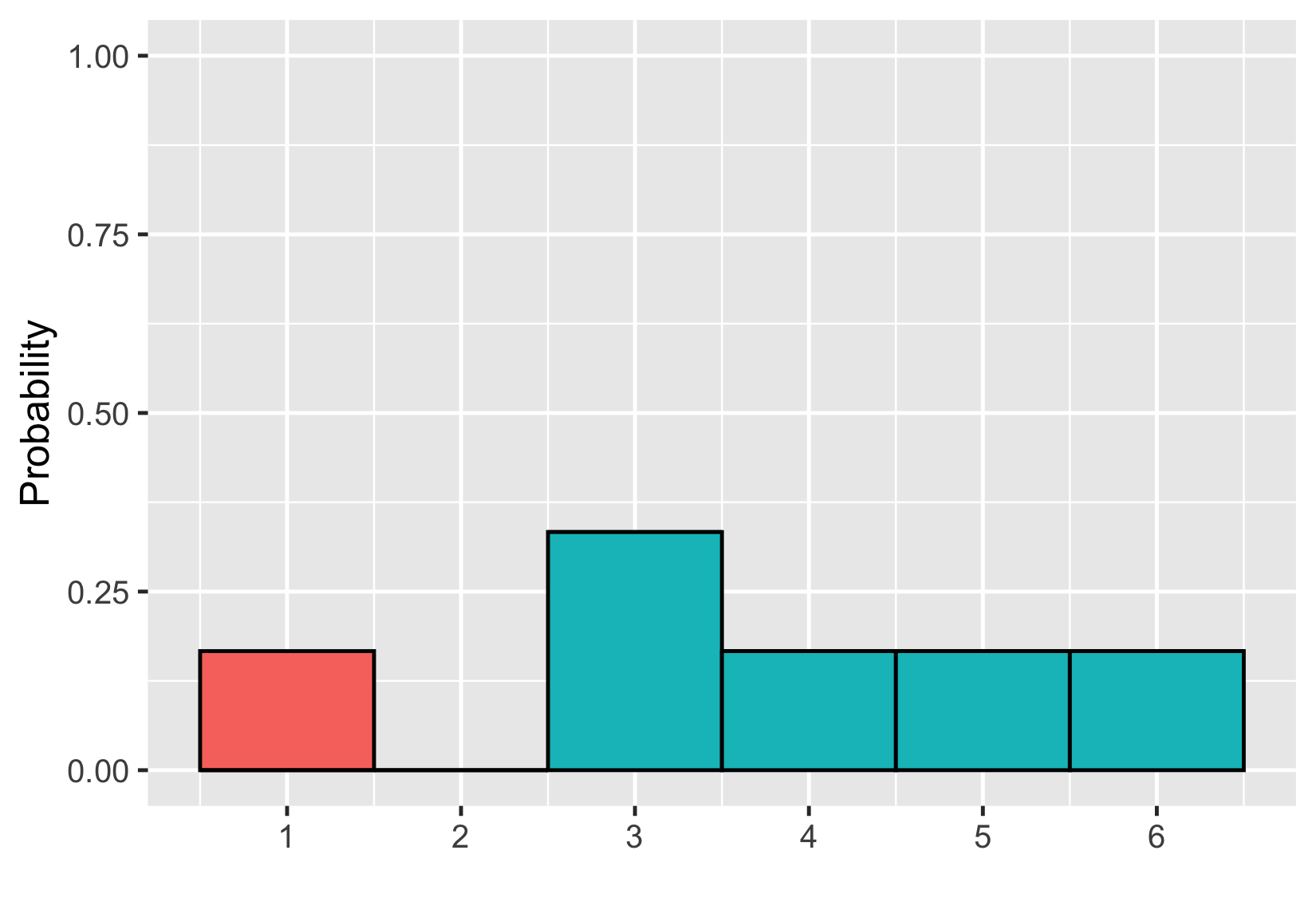
Addition d’aires
$$P(\text{uneven die roll}) \le 2 = 1/6$$
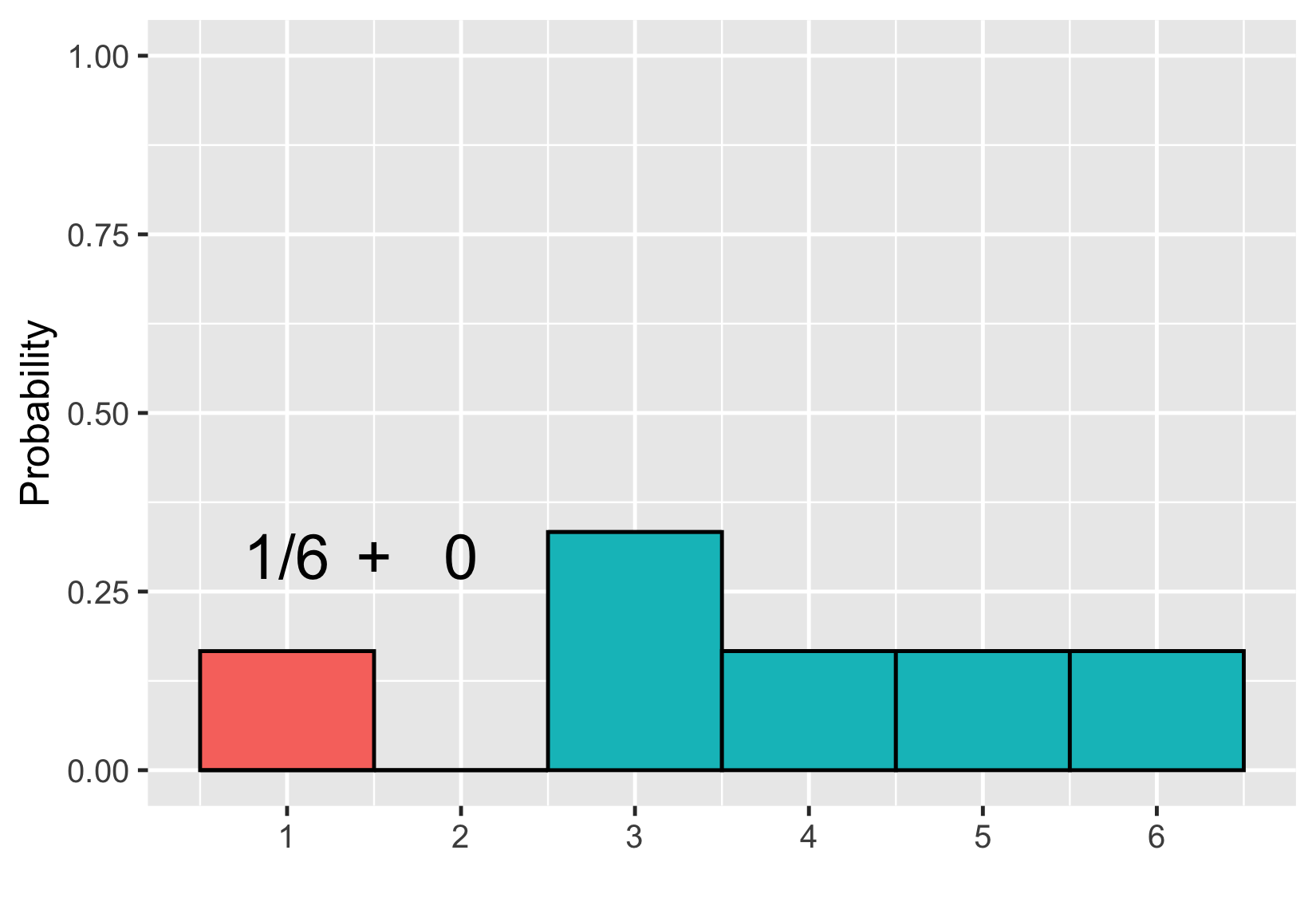
Distributions de probabilités discrètes
Décrit la probabilité de résultats discrets
Dé équitable
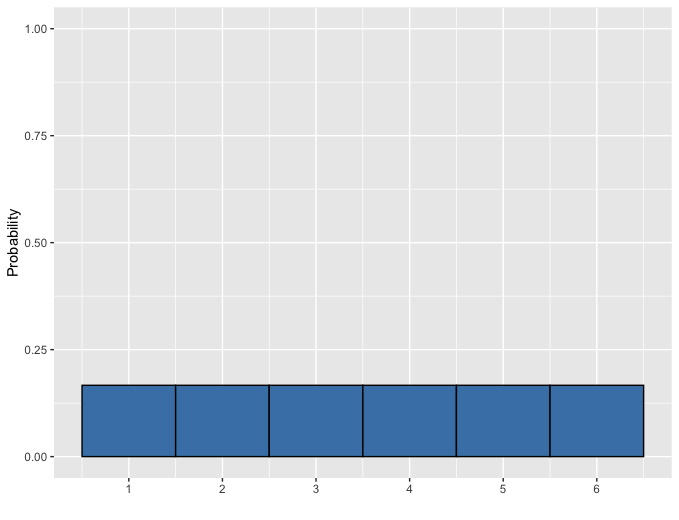
Distribution uniforme discrète
Dé irrégulier
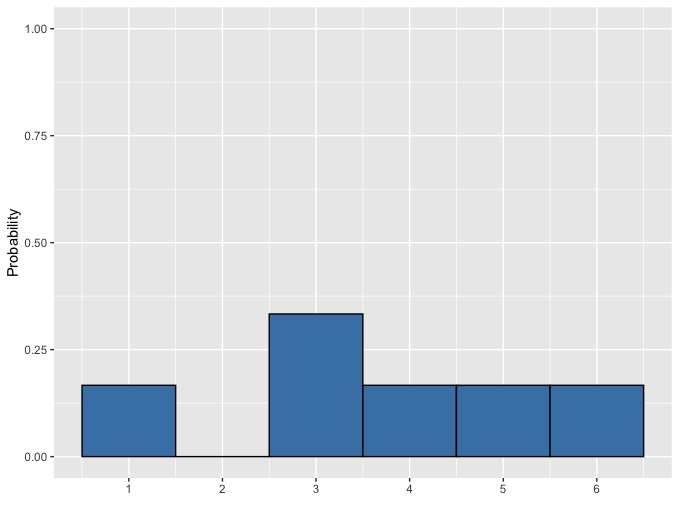
Échantillonnage à partir d'une distribution discrète
| Lancer | Résultat |
|---|---|
| 1 | 1 |
| 2 | 2 |
| 3 | 3 |
| 4 | 4 |
| 5 | 5 |
| 6 | 6 |
$ {Mean} = 3.5 $
| Lancer | Résultat |
|---|---|
| 1 | 3 |
| 2 | 1 |
| 3 | 2 |
| 4 | 4 |
| 5 | 6 |
| 6 | 3 |
| 7 | 2 |
| 8 | 2 |
| 9 | 2 |
| 10 | 5 |
Visualisation d’un échantillon
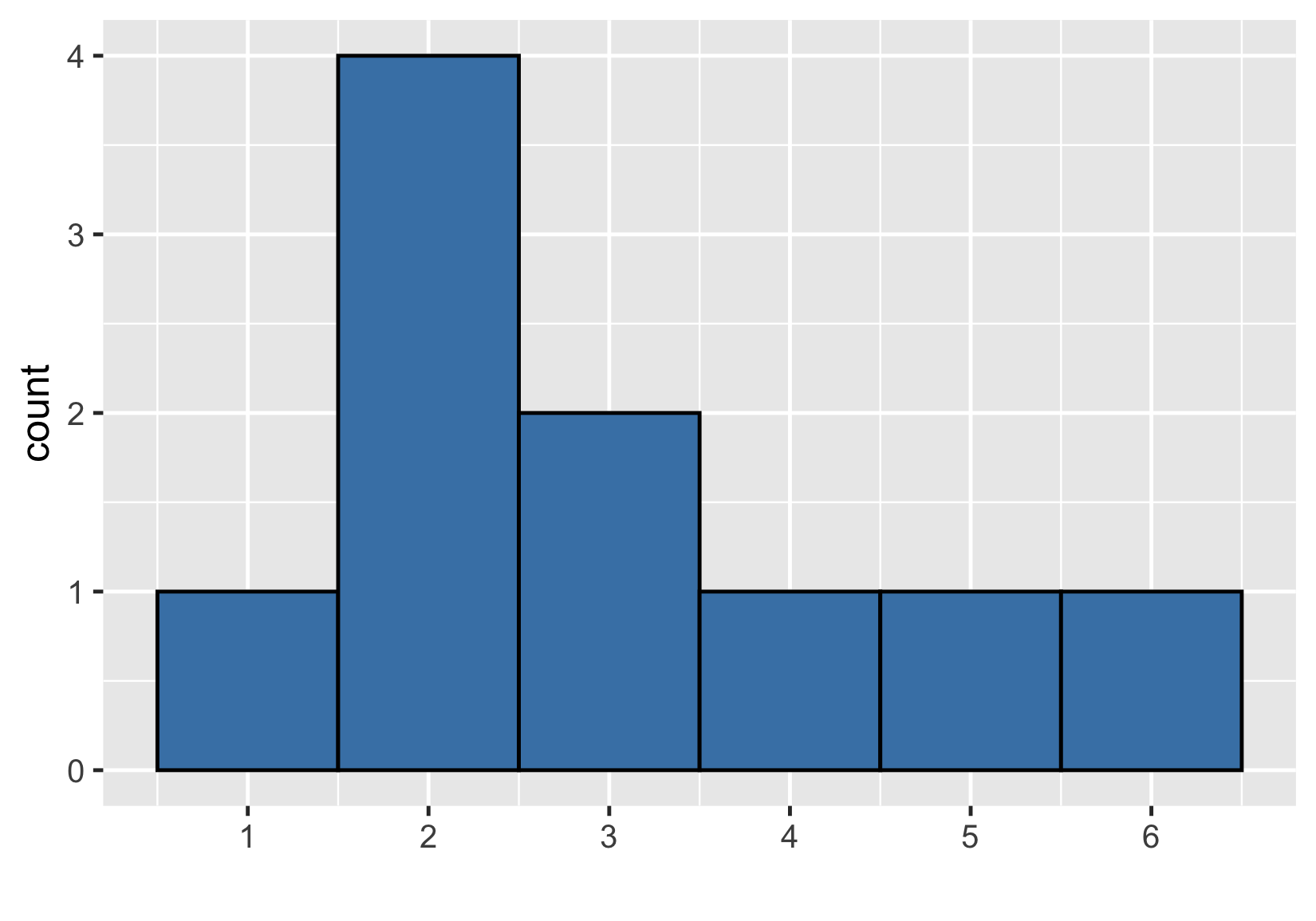
Distribution de l’échantillon vs distribution théorique

$ {Mean} = 3.0 $

$ {Mean} = 3.5 $
Un échantillon plus important
Échantillon de 100 lancers
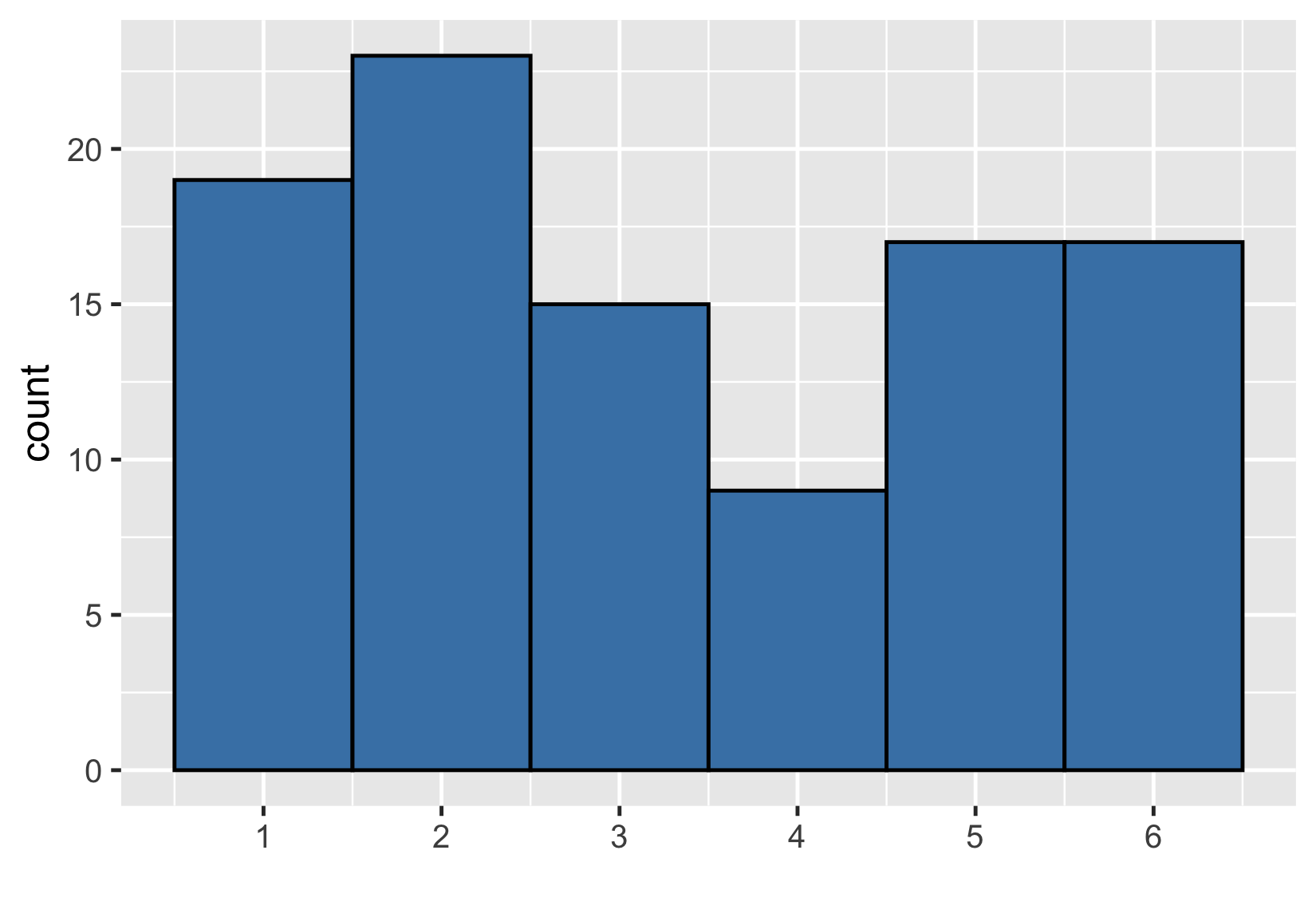
$ {Mean} = 3.33 $
Un échantillon encore plus important
Échantillon de 1000 lancers
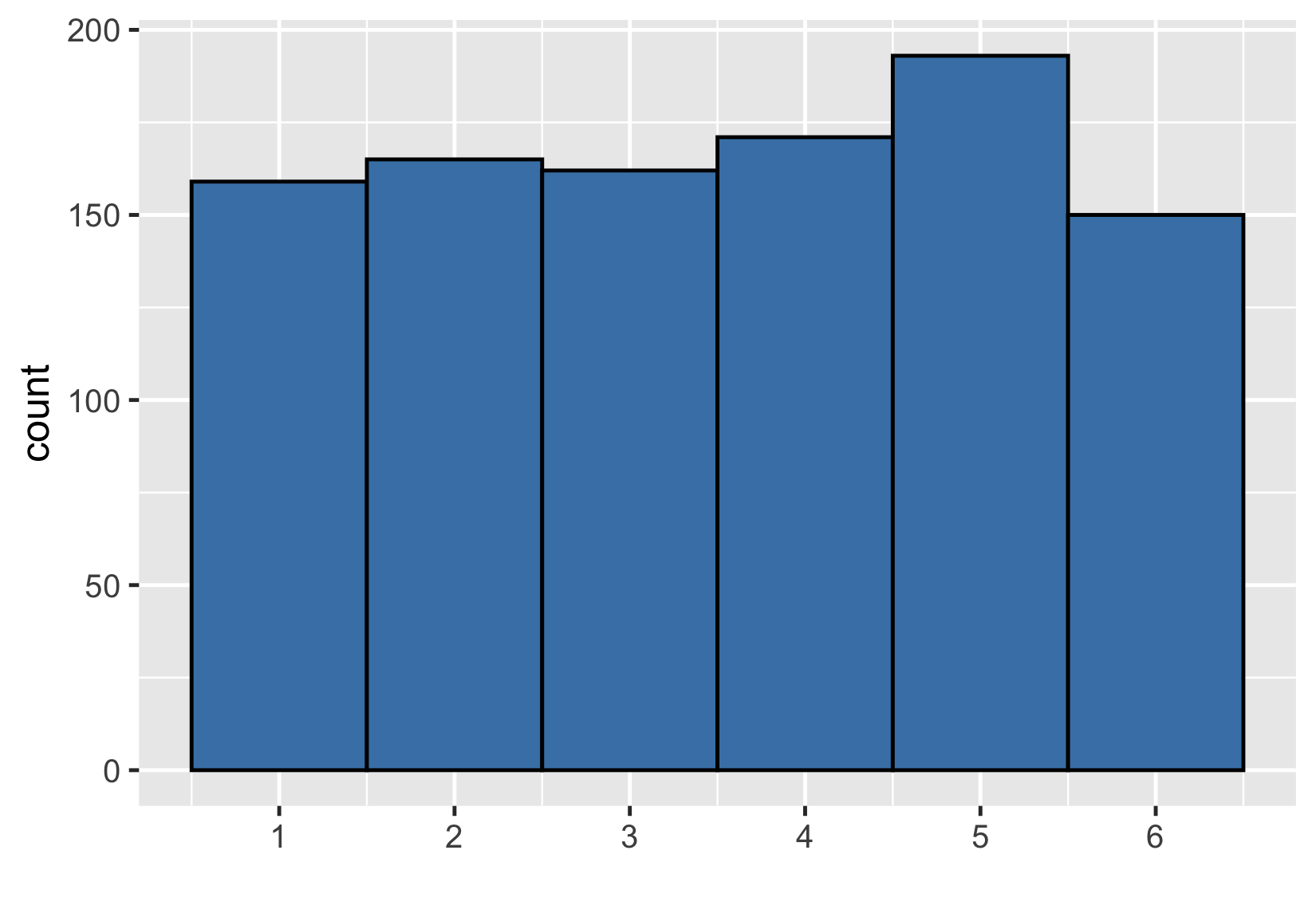
$ {Mean} = 3.52 $
La loi des grands nombres
Au fur et à mesure que la taille de votre échantillon augmente, la moyenne de l’échantillon se rapproche de la valeur attendue.
| Taille de l’échantillon | Moyenne |
|---|---|
| 10 | 3,00 |
| 100 | 3,33 |
| 1000 | 3,52 |
Passons à la pratique !
Introduction aux statistiques

