Probabilité conditionnelle
Introduction aux statistiques

George Boorman
Curriculum Manager, DataCamp
Plusieurs réunions
Échantillonnage sans remise

Plusieurs réunions
Échantillonnage sans remise
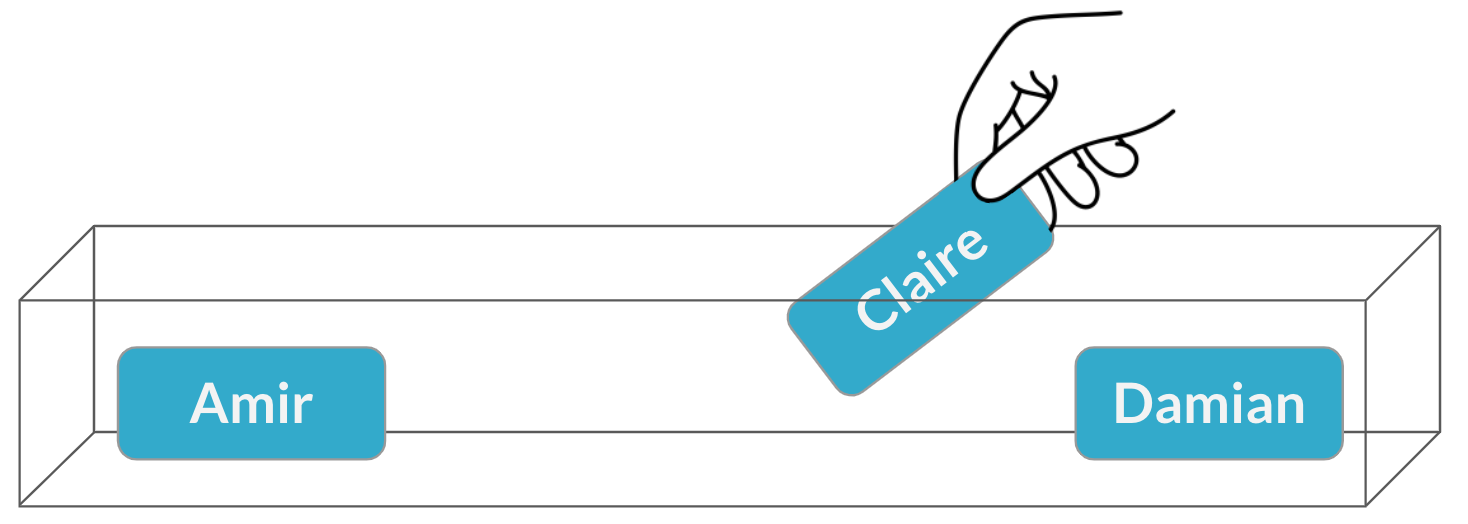
$$P(\text{Claire}) = \frac{1}{3} = 33\%$$
Événements dépendants
La probabilité du deuxième événement est influencée par le résultat du premier événement

Événements dépendants
La probabilité du deuxième événement est influencée par le résultat du premier événement
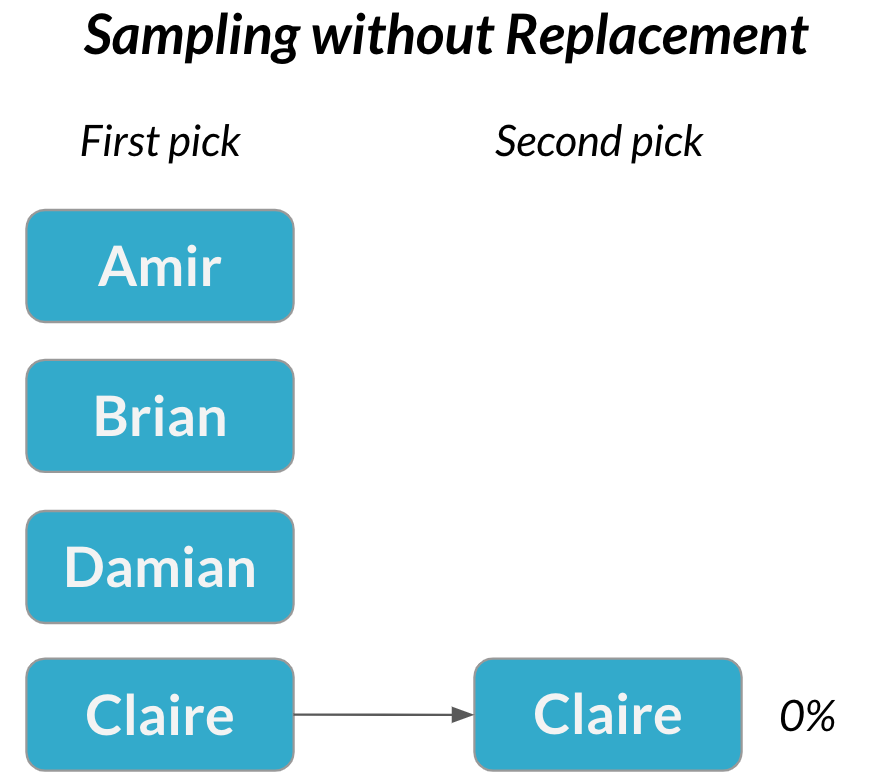
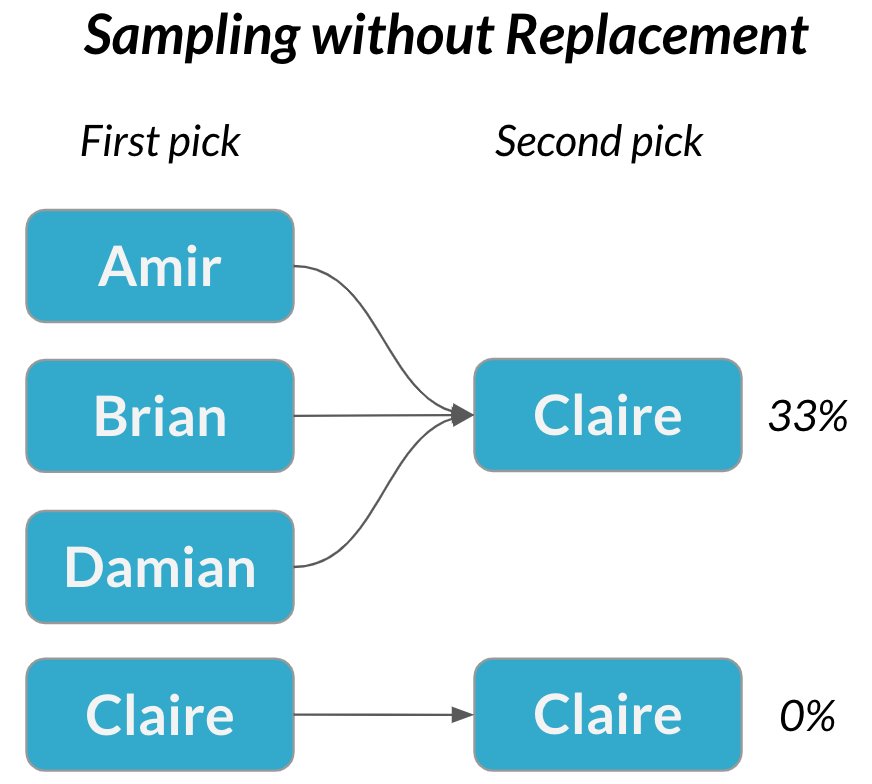
Événements dépendants
La probabilité du deuxième événement est influencée par le résultat du premier événement
Échantillonnage sans remise = chaque sélection est dépendante
Probabilité conditionnelle
La probabilité conditionnelle est utilisée pour calculer la probabilité d'événements dépendants
- La probabilité d'un événement dépend du résultat d'un autre événement

Diagrammes de Venn
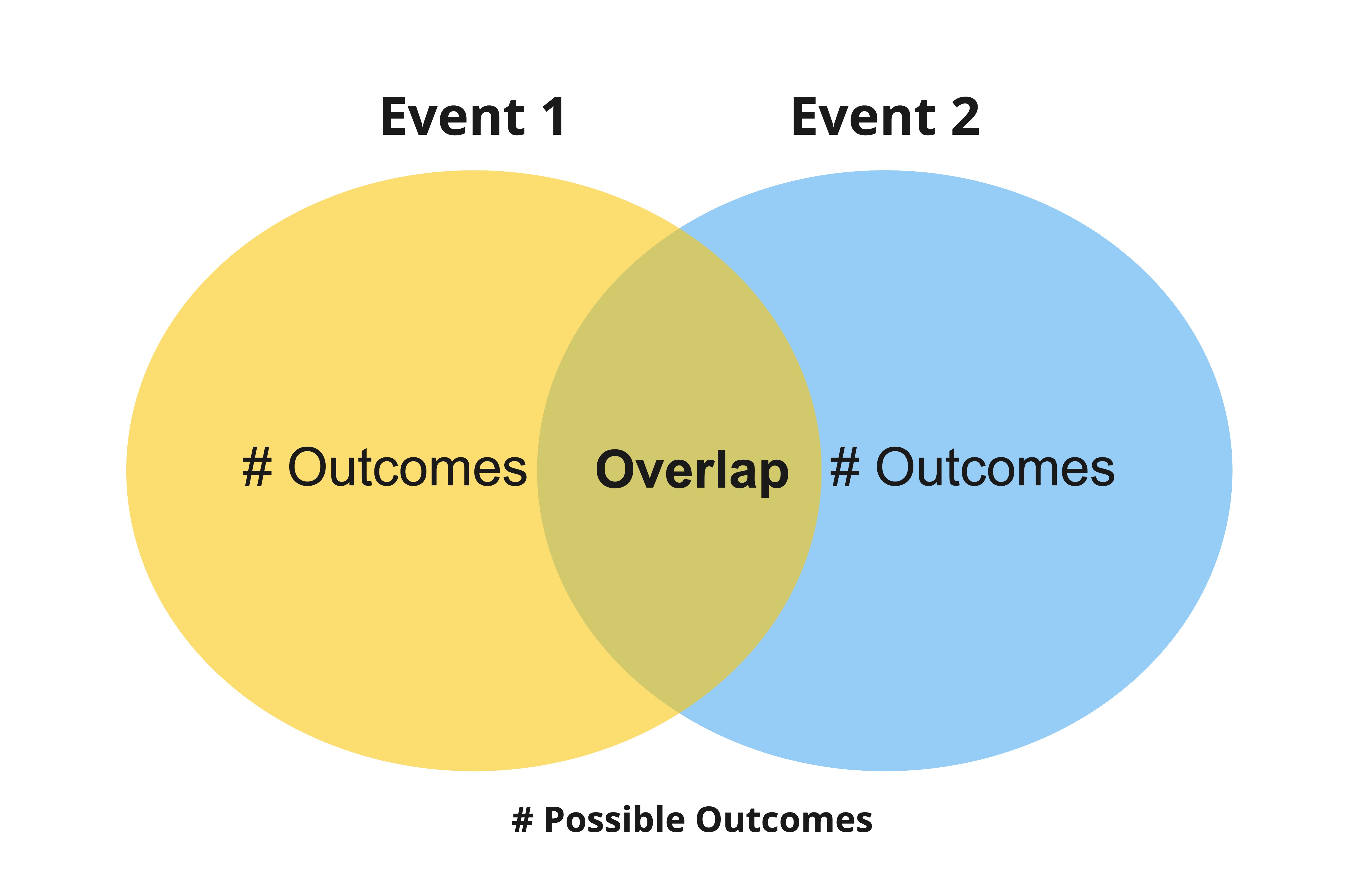
Ventes de cuisine supérieures à $150
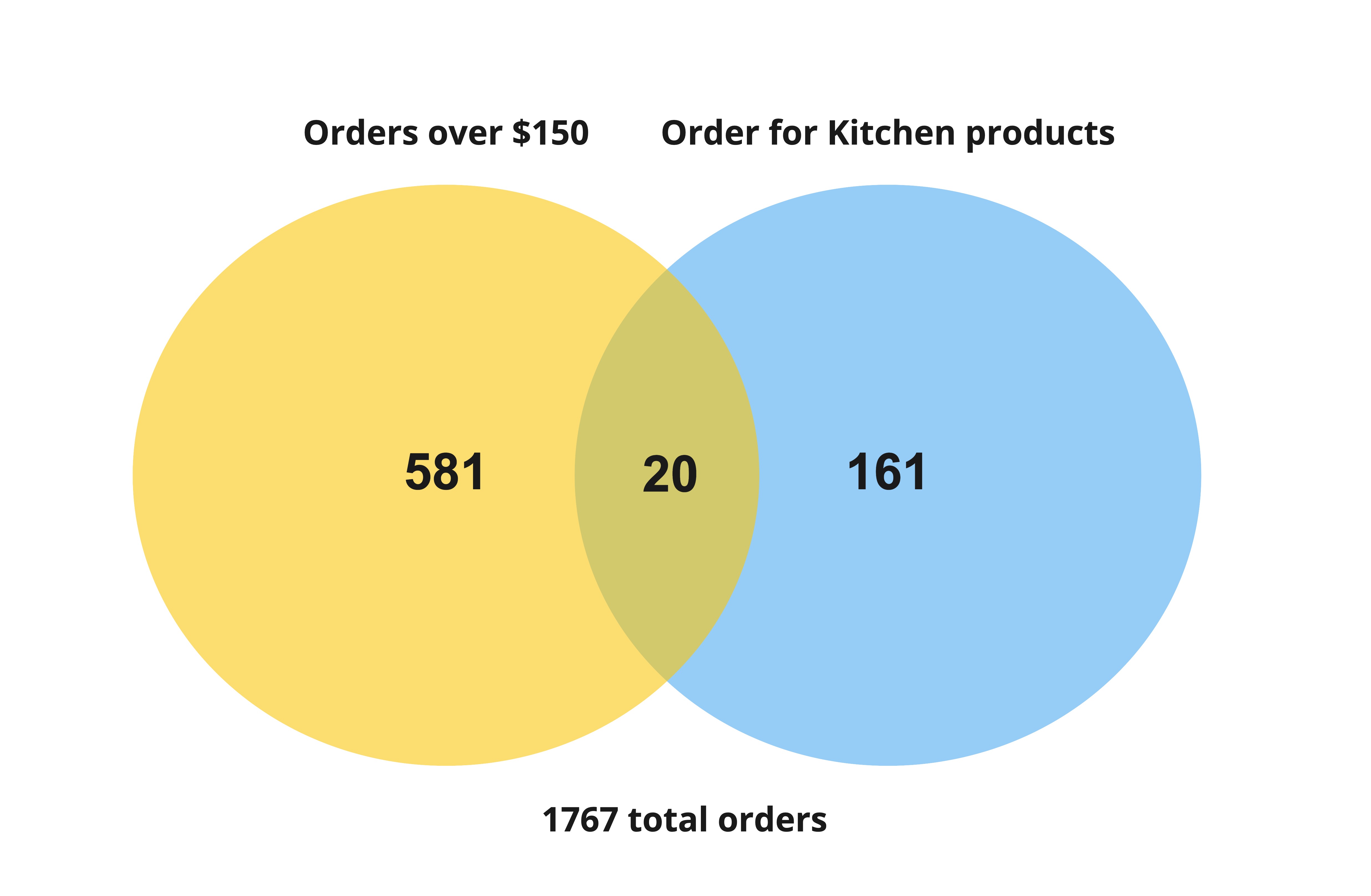
Ventes de cuisine supérieures à $150

$$P(Order > 150 | Kitchen) = \frac{\frac{20}{1767}}{\frac{181}{1767}}$$
$$P(Order > 150 | Kitchen) = \frac{20}{181} $$
L'ordre des événements est important
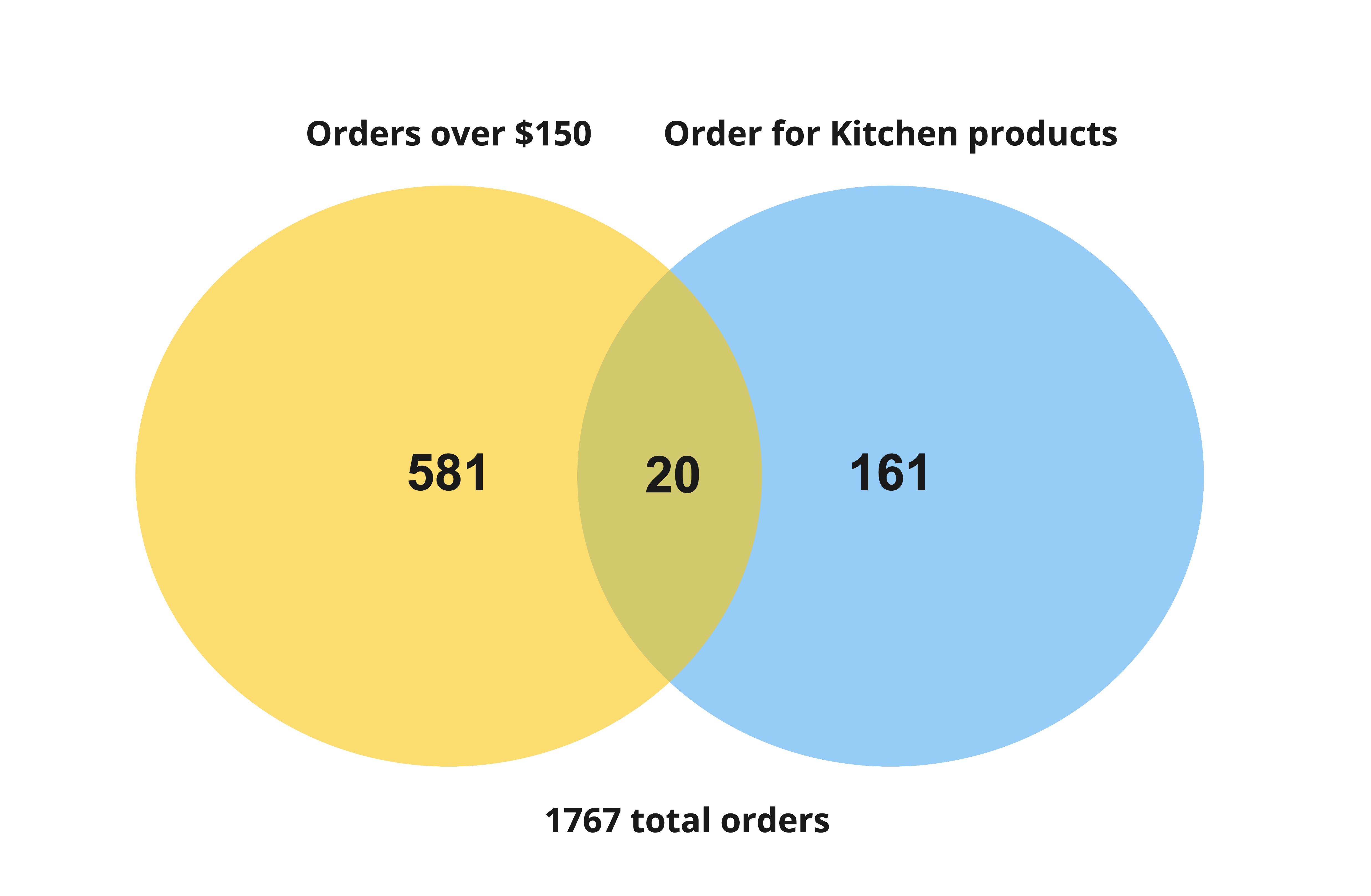
$$P(Kitchen | Order > 150) = \frac{\frac{20}{1767}}{\frac{601}{1767}}$$
$$P(Kitchen | Order > 150) = \frac{20}{601} $$
Formule de probabilité conditionnelle
$$P(A | B) = \frac{{P(A \ \cap \ B)}}{{P(B)}}$$
$P(A | B)$ → Probabilité de l'événement A, selon l'événement B
$P(A \ \cap \ B)$ → Probabilité que l'événement A et l'événement B se produisent
- Divisée par la probabilité de l'événement B → $P(B)$
Passons à la pratique !
Introduction aux statistiques

