Mesures de dispersion
Introduction aux statistiques

George Boorman
Curriculum Manager, DataCamp
Qu’est-ce que la dispersion ?
Pourquoi la dispersion est-elle importante ?
- La dispersion mesure la variété de nos données
Les t-shirts coûtent généralement $30
- Le coût peut varier entre 10 et 200 $
- Quelle est la probabilité qu'un produit coûte 30 $ ?
Si les t-shirts coûtaient entre 20 et 50 $
- Cela modifie-t-il la probabilité d'en trouver un pour 30 $ ?

1 Crédit d'image : https://unsplash.com/@uyk
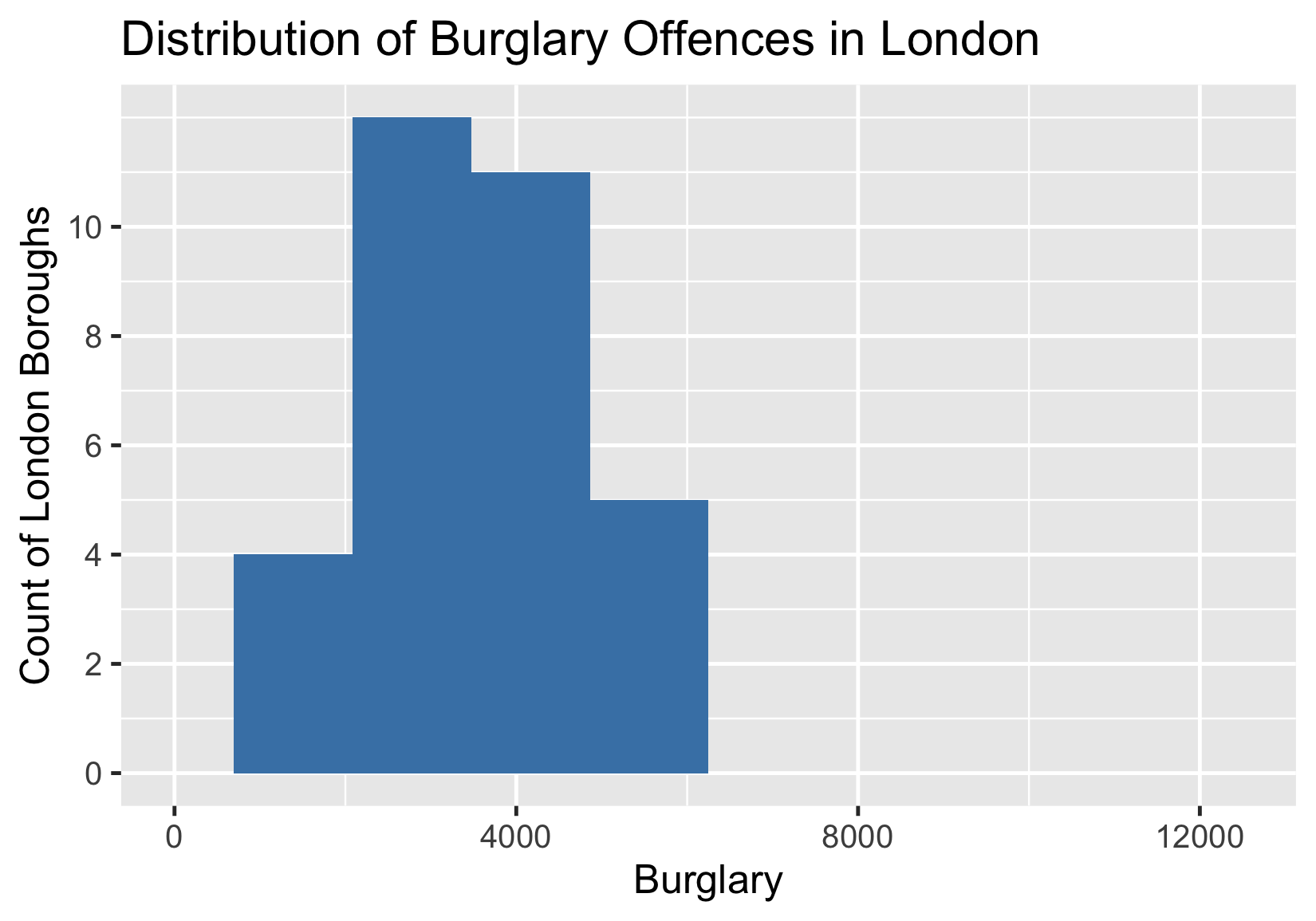
Étendue
${range} = maximum - minimum$
${range(Burglaries)} = 5 183 - 1 432$
${range(Burglaries)} = 3 751$
| Arrondissement | Cambriolage |
|---|---|
| Tower Hamlets | 5 183 |
| Hackney | 5 079 |
| Barnet | 5 067 |
| … | … |
| Sutton | 1 815 |
| Bexley | 1 583 |
| Kingston sur Tamise | 1 432 |
Variance
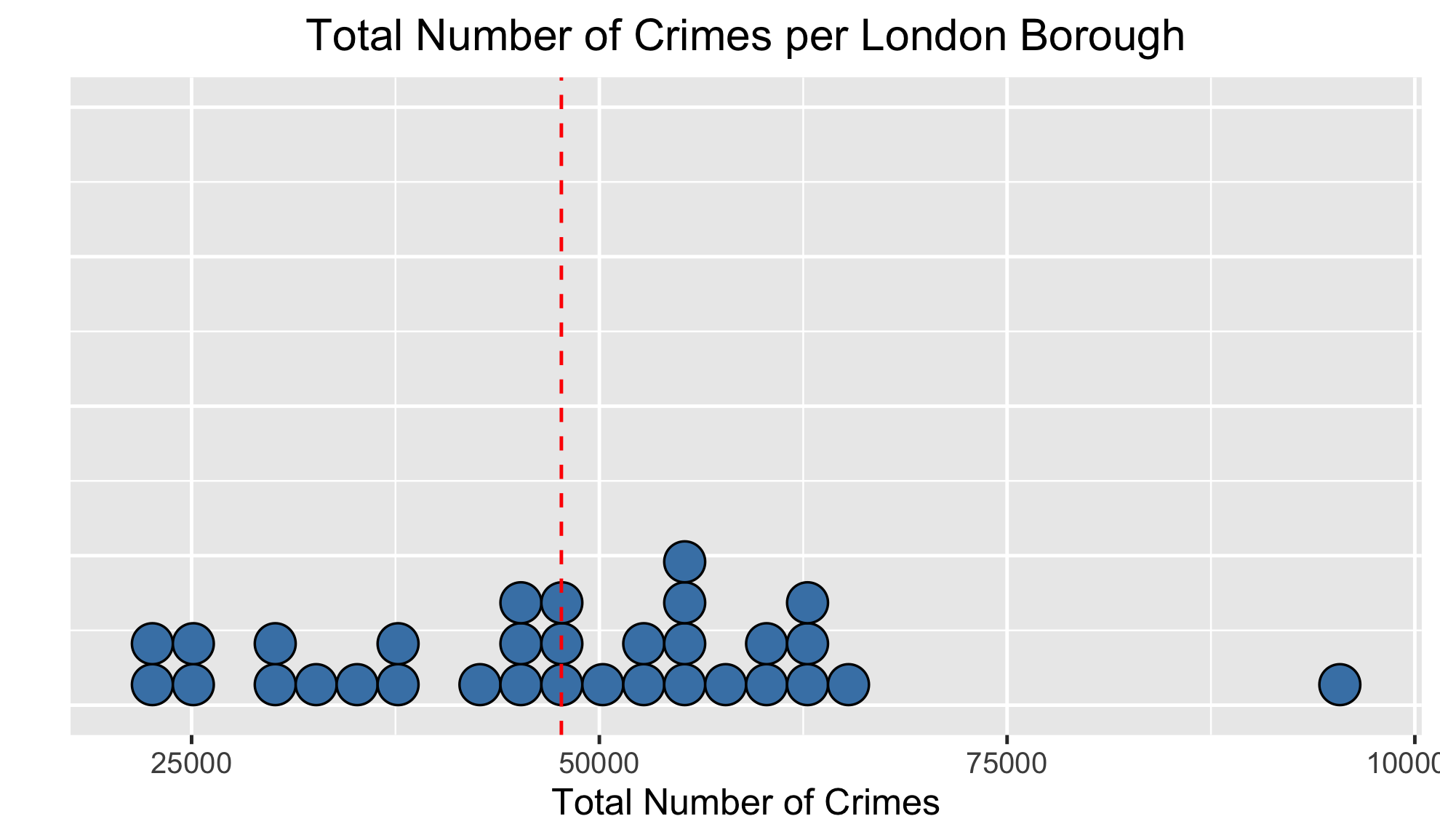
Variance
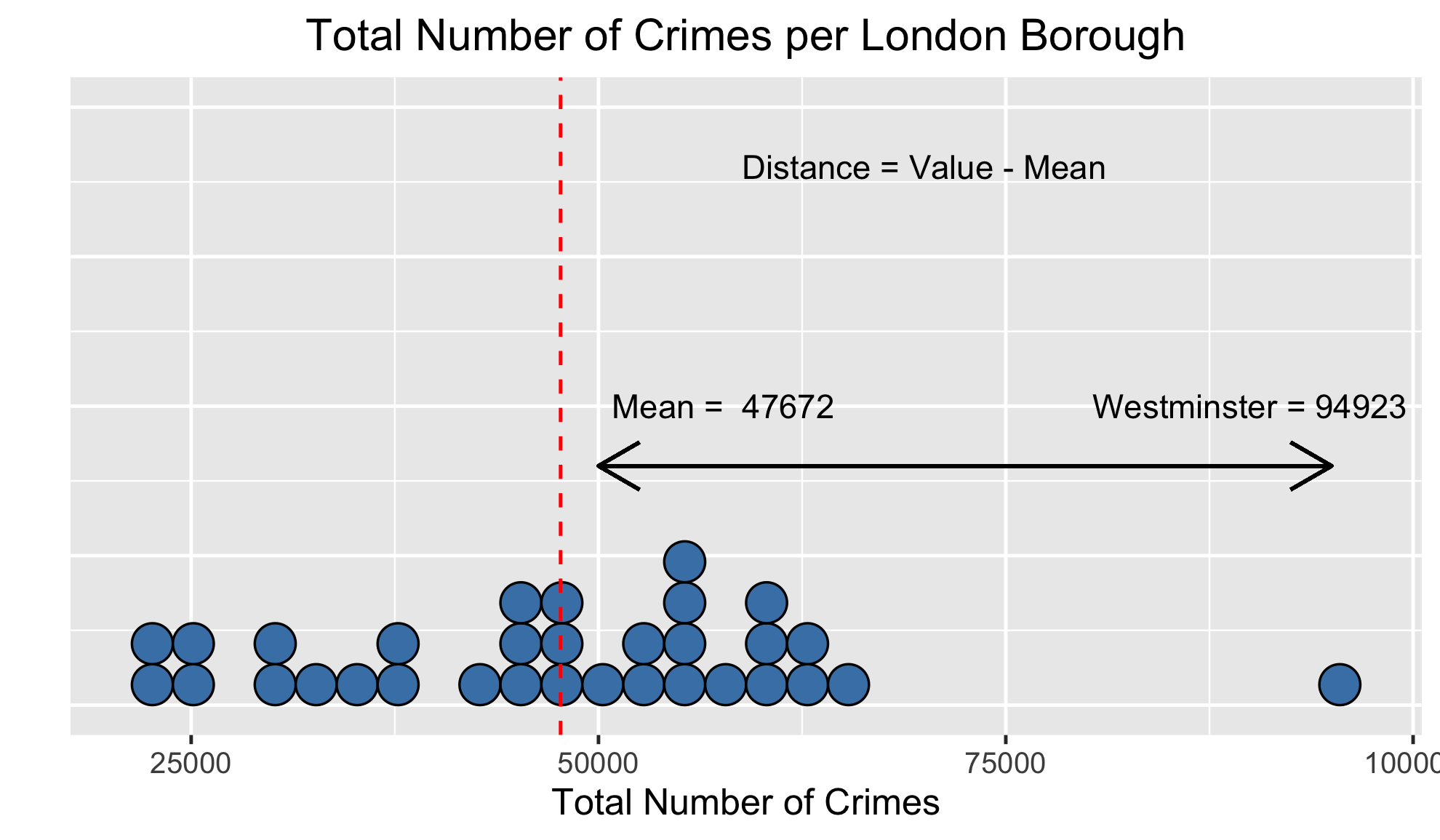
Variance
| Arrondissement | Total des crimes | Moyenne | Distance |
|---|---|---|---|
| Barking et Dagenham | 37 939 | 47 672 | -9 733 |
| Barnet | 52 421 | 47 672 | 4 749 |
| Bexley | 29 285 | 47 672 | -18 387 |
| Brent | 55 465 | 47 672 | 7 793 |
| Bromley | 42 982 | 47 672 | -4 690 |
| Camden | 54 806 | 47 672 | 7 134 |
| … | … | … | … |
| Total | 1 525 492 | 1 525 492 | 0 |
Variance
| Arrondissement | Total des crimes | Moyenne | Distance | Distance au carré |
|---|---|---|---|---|
| Barking et Dagenham | 37 939 | 47 672 | -9 733 | 94 731 289 |
| Barnet | 52 421 | 47 672 | 4 749 | 22 553 001 |
| Bexley | 29 285 | 47 672 | -18 387 | 338 081 769 |
| Brent | 55 465 | 47 672 | 7 793 | 60 730 849 |
| Bromley | 42 982 | 47 672 | -4 690 | 21 996 100 |
| Camden | 54 806 | 47 672 | 7 134 | 50 893 956 |
| … | … | … | … | … |
| Total | 1 525 492 | 1 525 492 | 0 | 7 509 750 824 |
Variance
$${variance(total \ crime)} = \frac{7 509 750 824}{32}$$
$${variance(total \ crime)} = \ 234 679 713$$
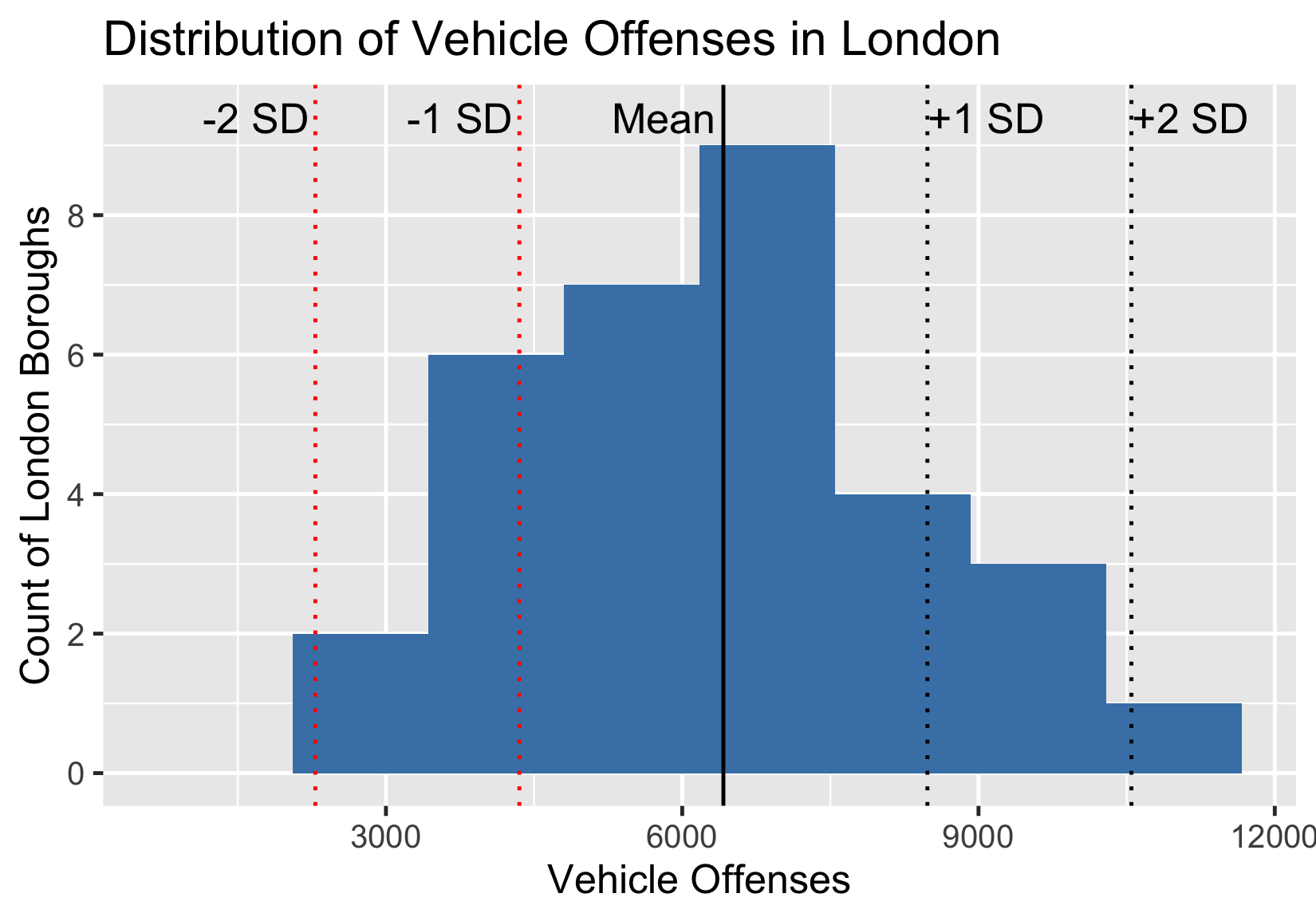
Écart-type
${standard \ deviation(total \ crime)} = {\sqrt( variance(total \ crime))}$
${standard \ deviation(total \ crime)} = {\sqrt(234,679,713)}$
${standard \ deviation(total \ crime)} = 15,319.26$
- Écart-type proche de zéro = données regroupées autour de la moyenne
Écart-type dans un histogramme
Quartiles
- Quartiles :
- diviser les données en quatre parties égales
| Crime | 0 % | 25 % | 50 % | 75 % | 100 % |
|---|---|---|---|---|---|
| Cambriolage | 1 432,00 | 2 681,75 | 3 416,50 | 4 392,00 | 5,183.00 |
| Vol qualifié | 363.00 | 895.75 | 1 354,50 | 1 976,50 | 4 156,00 |
| Vol | 4 090,00 | 7 739,75 | 9 624,00 | 12 059,00 | 40 278,00 |
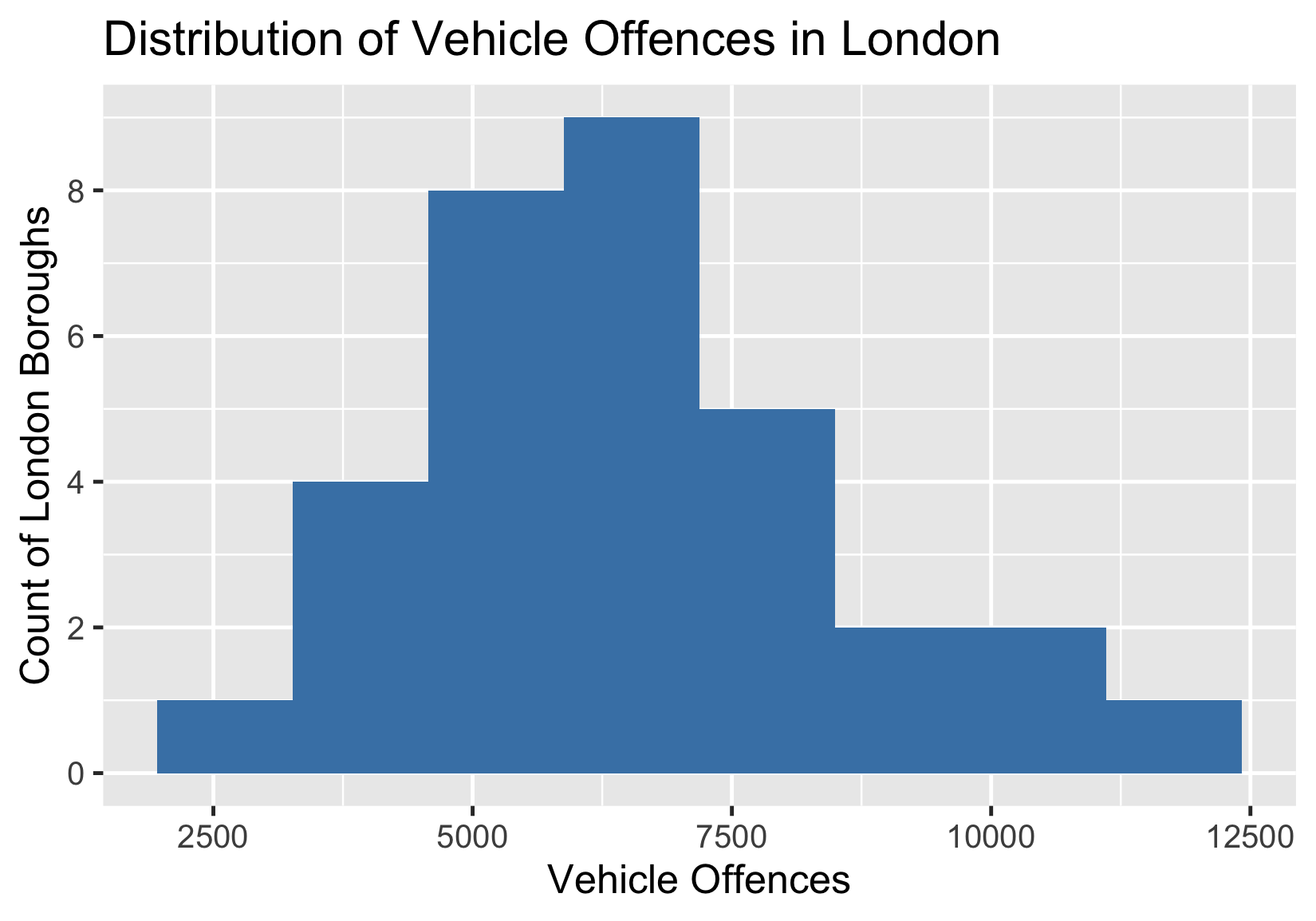
| Infractions liées aux véhicules | 2 143,00 | 4 838,25 | 6 424,50 | 7 520,75 | 11 292,00 |
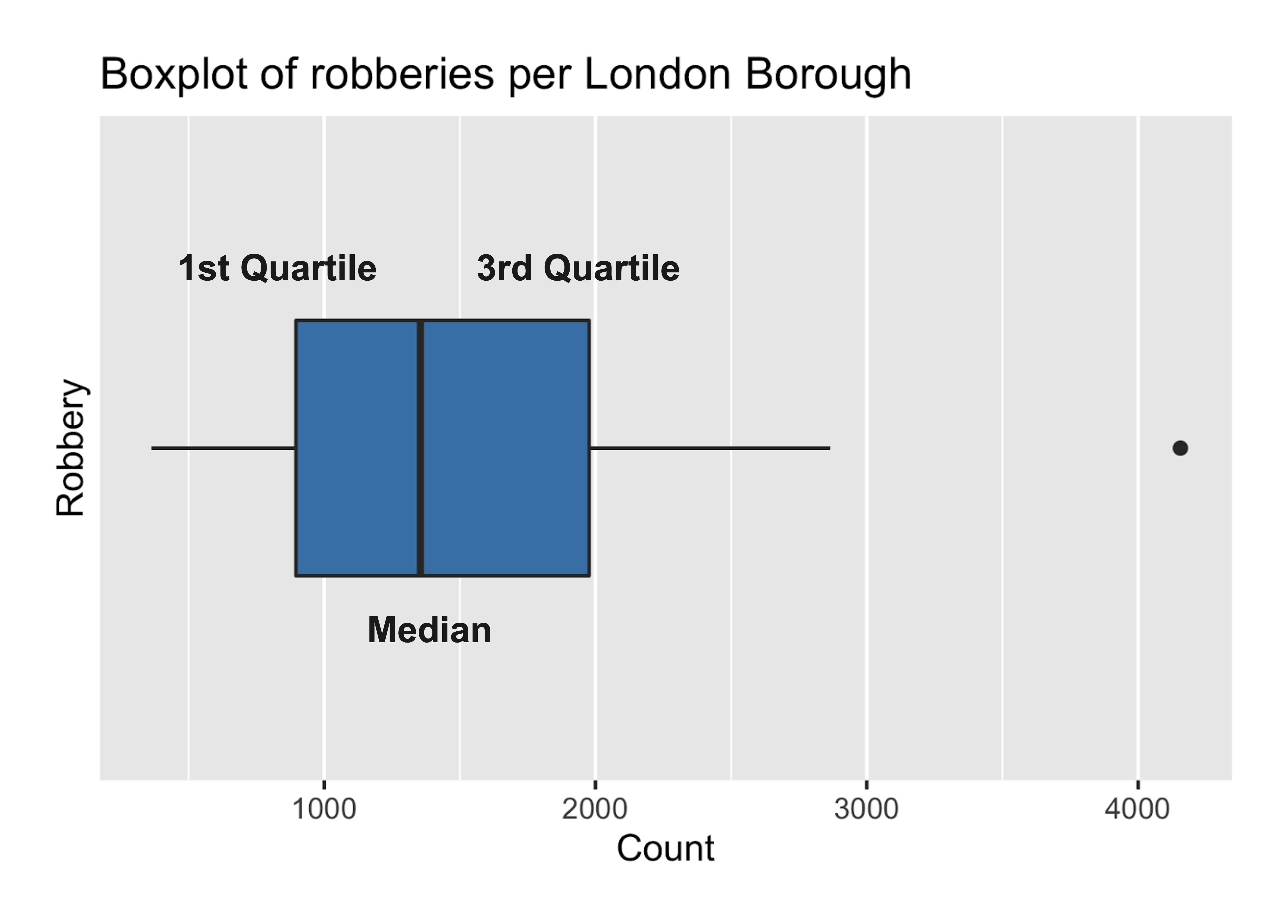
Quartiles
- Quartiles :
- diviser les données en quatre parties égales
| Crime | 0 % | 25 % | 50 % | 75 % | 100 % |
|---|---|---|---|---|---|
| Cambriolage | 1 432,00 | 2 681,75 | 3 416,50 | 4 392,00 | 5,183.00 |
| Vol qualifié | 363.00 | 895.75 | 1 354,50 | 1 976,50 | 4 156,00 |
| Vol | 4 090,00 | 7 739,75 | 9 624,00 | 12 059,00 | 40 278,00 |
| Infractions liées aux véhicules | 2 143,00 | 4 838,25 | 6 424,50 | 7 520,75 | 11 292,00 |
- Deuxième quartile (50 %) = médiane
Diagrammes en boîte
Intervalle interquartile (IQR)
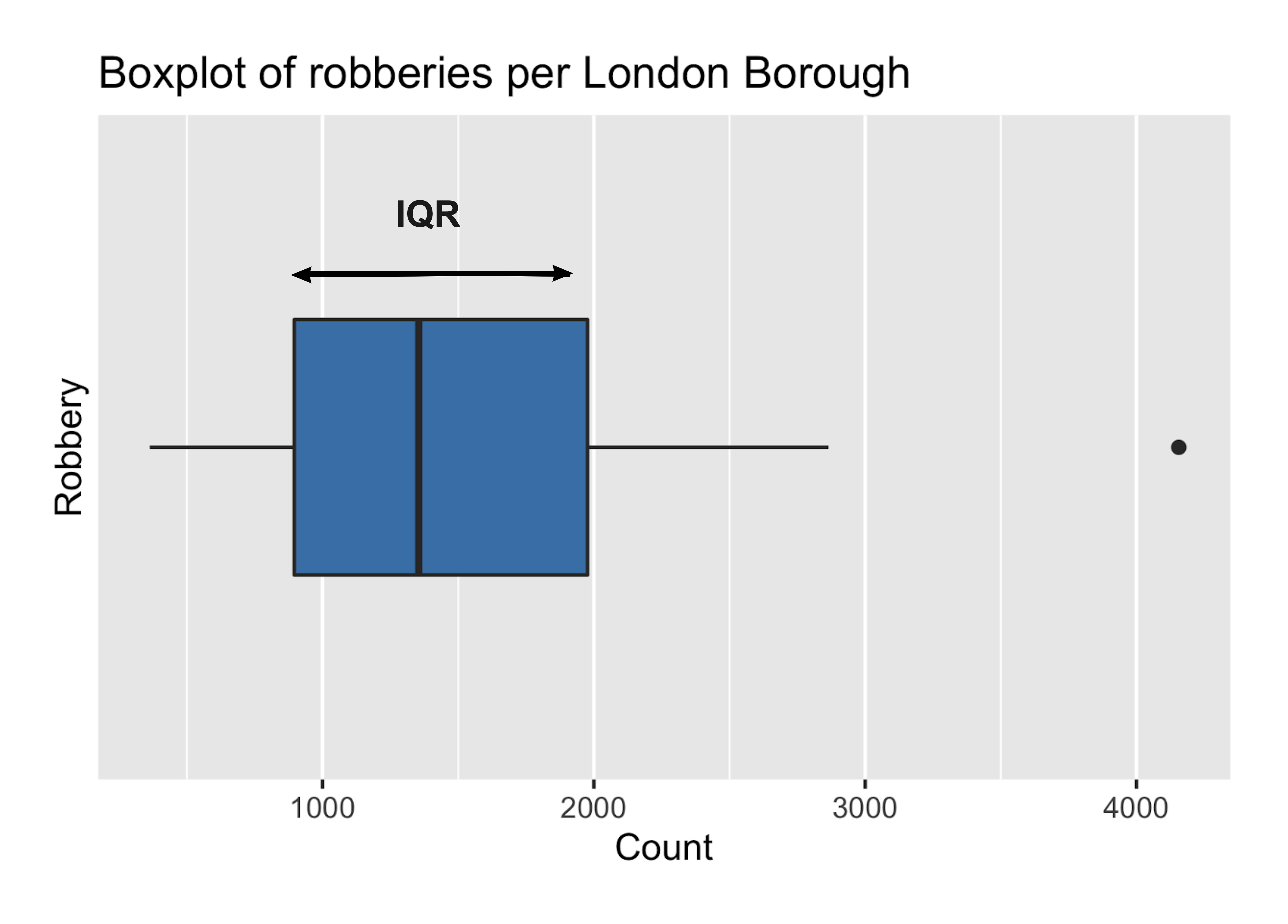
- L'IQR est moins affecté par les valeurs extrêmes
IQR = 3e quartile - 1er quartile
IQR = 1976,50 - 895,75
IQR = 1080,75
Passons à la pratique !
Introduction aux statistiques

