Quelles sont les chances ?

Introduction aux statistiques

George Boorman

Curriculum Manager, DataCamp

Mesurer les chances

Quelle est la probabilité d’un événement ?

$$ P(\text{event}) = \frac{\text{\# ways event can happen}}{\text{total \# of possible outcomes}} $$

Exemple : pile ou face

$$ P(\text{heads}) = \frac{\text{1 way to get heads}}{\text{2 possible outcomes}} = \frac{1}{2} = 50\%$$

line of probability from left where 0 percent = impossible, to right where 100 percent = will certainly happen.png

Introduction aux statistiques

Affectation des vendeurs

Box with Amir, Brian, Claire, and Damian's names.png

  • Échantillonnage
Introduction aux statistiques

Affectation des vendeurs

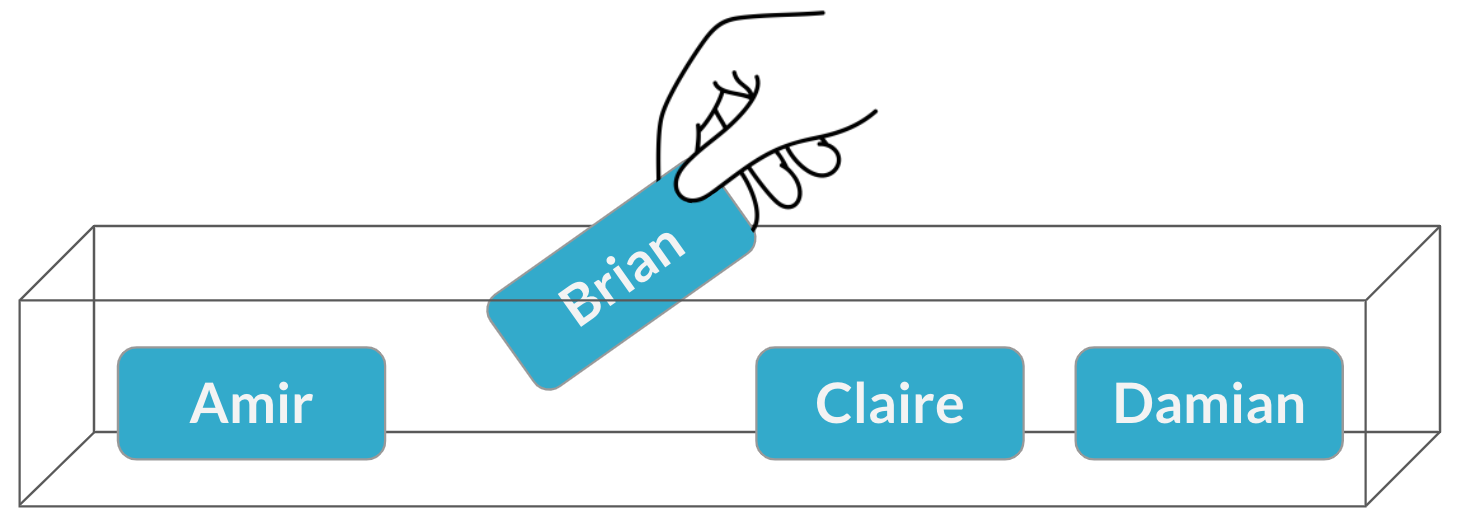
Pulling out Brian's name from the box.png

$$P(\text{Brian}) = \frac{1}{4} = 25\%$$

Introduction aux statistiques

Réunion matinale

Pulling out Brian's name from the box.png

Introduction aux statistiques

Réunion de l'après-midi

Pulling out Brian's name from the box.png

$$P(\text{Brian}) = \frac{1}{4} = 25\%$$

  • Échantillonnage avec remise
Introduction aux statistiques

Probabilité indépendante

Deux événements sont indépendants si la probabilité du deuxième événement ne change pas en fonction du résultat du premier événement.

Introduction aux statistiques

Ventes au détail en ligne

Numéro de commande Type de produit Quantité nette Chiffre d'affaires brut Réductions Retours Chiffre d'affaires net
200 Panier 13 3 744,0 -316,80 0,00 3 427,20
201 Panier 12 3 825,0 -201,60 -288,0 3 335,40
202 Panier 17 3 035,0 -63,25 0,00 2 971,75
203 Art et sculpture 47 2 696,8 -44,16 0,00 2 652,64
204 Panier 17 2 695,0 -52,50 -110,00 2 532,50

wooden_baskets.jpg

1 Crédit d'image : https://unsplash.com/@rodriguezedm
Introduction aux statistiques

Probabilité de passer une commande pour un produit de joaillerie

Type de produit Nombre de commandes
Panier 551
Art et sculpture 337
Bijoux 210
Cuisine 161
Décoration d'intérieur 131
… …
Total 1 767
Introduction aux statistiques

Probabilité de passer une commande pour un produit de joaillerie

$$P(Jewelry) = \frac{Order \ Count(Jewelry)}{Sum(Total \ Order \ Count)}$$

$$P(Jewelry) = \frac{210}{1767}$$

$$P(Jewelry) = 11.88 %$$

Introduction aux statistiques

Probabilités pour tous les types de produits

Type de produit Nombre de commandes Probabilité
Panier 551 31,18 %
Art et sculpture 337 19,07 %
Bijoux 210 11,88 %
Cuisine 161 9,11 %
Décoration d'intérieur 131 7,41 %
… … …
Total 1 767 100 %
Introduction aux statistiques

Passons à la pratique !

Introduction aux statistiques

Preparing Video For Download...