Big-O notation: time complexity

Optimizing Code in Java

Pavlos Kosmetatos

Lead Engineer @Wealthyhood

What is time complexity?

Time Complexity: Measure of how runtime grows with input size
Helps answer: "What happens when my data gets 10× larger?"
Does not focus on absolute time

Big-O notation

Mathematical notation to describe worst-case scenario.

Some common complexity classes:

O(1): Constant time - size-independent

Understanding O(1)

An example of a O(1) operation is ArrayList's get()

Internal (simplified) implementation for an ArrayList that holds Strings:

public class ArrayList {}
    private String[] data; // Internal array
    private int size;

    // Get operation - direct array access
    public String get(int index) {
        return data[index]; // O(1)
    }
}

Big-O notation

Mathematical notation to describe worst-case scenario

Some common complexity classes:

O(1): Constant time - size-independent
O(n): Linear time - grows with input size

Understanding O(n)

A similar example, but for ArrayList's contains()

public boolean contains(Object o) {
    return indexOf(o) >= 0;
}

public int indexOf(Object o) {
    // Linear search through array
    for (int i = 0; i < size; i++) {
        if (o.equals(elementData[i])) {
            return i;
        }
    }
    return -1; // Not found
}

Big-O notation

Mathematical notation to describe worst-case scenario

Some common complexity classes:

O(1): Constant time - size-independent
O(n): Linear time - grows with input size
O(n²): Quadratic time - grows quadratically with input size

A practical example with quadratic complexity

// Finding a pair of numbers that sum to a target value
// Time complexity: O(n²)

public int[] findPairWithSum(ArrayList<Integer> numbers, int targetSum) {
    for (int i = 0; i < numbers.size(); i++) {
        for (int j = i + 1; j < numbers.size(); j++) {
            if (numbers.get(i) + numbers.get(j) == targetSum) {
                console.log("Found them!")
            }
        }
    }
}

Why time complexity matters

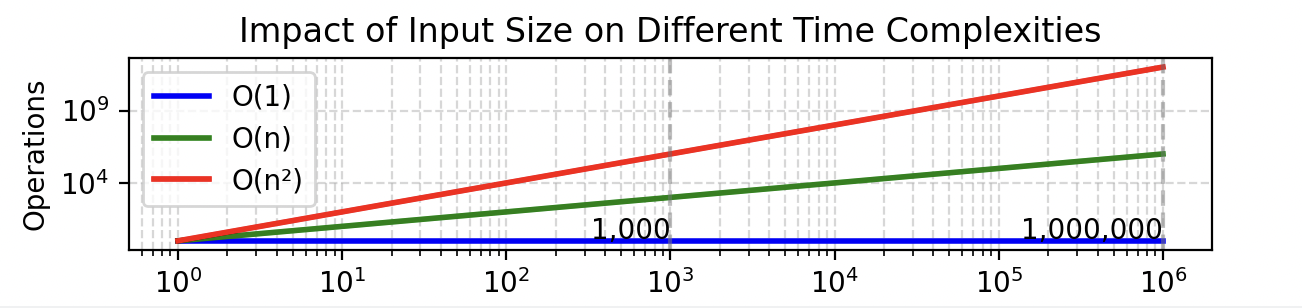
Input size impact:

O(1): 1,000 -> 1,000,000 items = Same time!
O(n): 1,000 -> 1,000,000 items = 1,000× slower
O(n²): 1,000 -> 1,000,000 items = 1,000,000× slower

Screenshot 2025-05-10 at 2.27.06?PM.png

Let's practice!

Optimizing Code in Java