Quelles sont les chances ?
Introduction aux statistiques en Python

Maggie Matsui
Content Developer, DataCamp
Mesurer les chances
Quelle est la probabilité d’un événement ?
$$ P(\text{événement}) = \frac{\text{nombre de manières d'obtenir l'événement}}{\text{nombre total de résultats possibles}} $$
Exemple : pile ou face
$$ P(\text{face}) = \frac{\text{1 manière d'obtenir face}}{\text{2 résultats possibles}} = \frac{1}{2} = 50 \%$$

Affectation des vendeurs
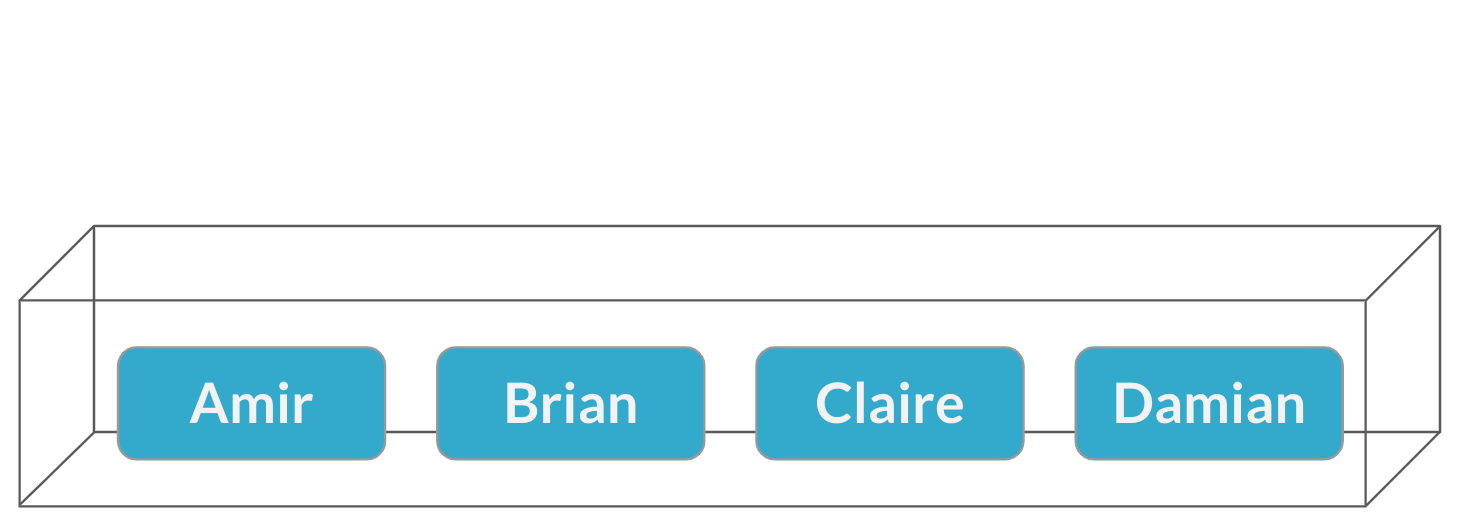
Affectation des vendeurs
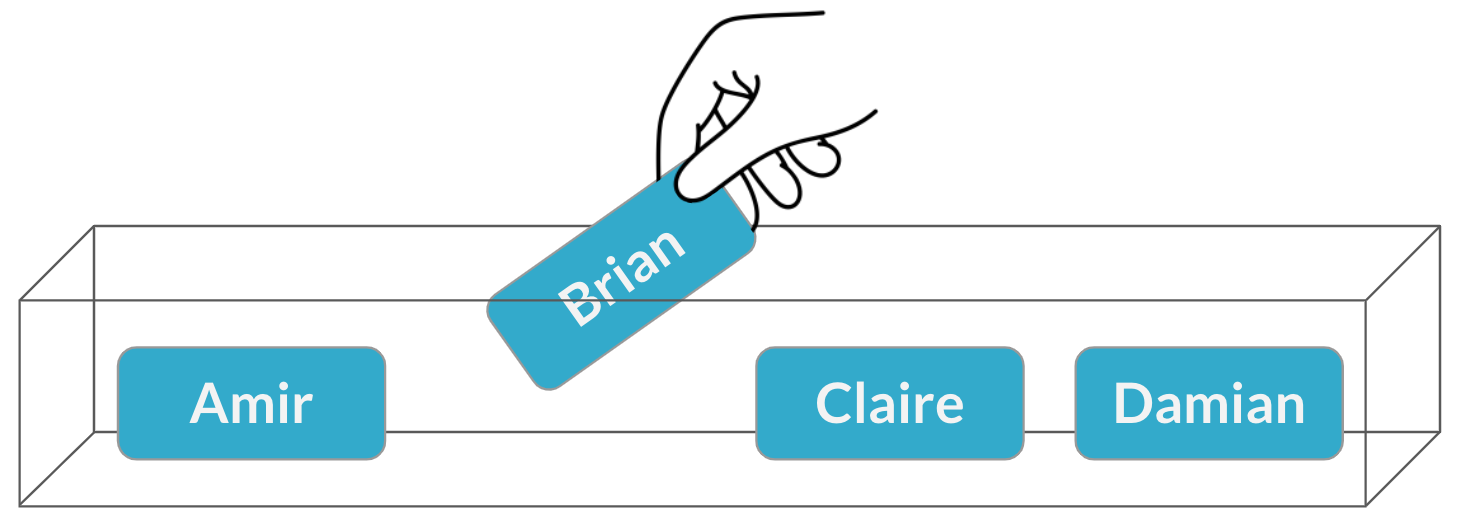
$$P(\text{Brian}) = \frac{1}{4} = 25 \%$$
Echantillonnage à partir d’un DataFrame
print(sales_counts)
name n_sales
0 Amir 178
1 Brian 128
2 Claire 75
3 Damian 69
sales_counts.sample()
name n_sales
1 Brian 128
sales_counts.sample()
name n_sales
2 Claire 75
Définition d’une graine aléatoire
np.random.seed(10)sales_counts.sample()
name n_sales
1 Brian 128
np.random.seed(10)
sales_counts.sample()
name n_sales
1 Brian 128
np.random.seed(10)
sales_counts.sample()
name n_sales
1 Brian 128
Une deuxième réunion
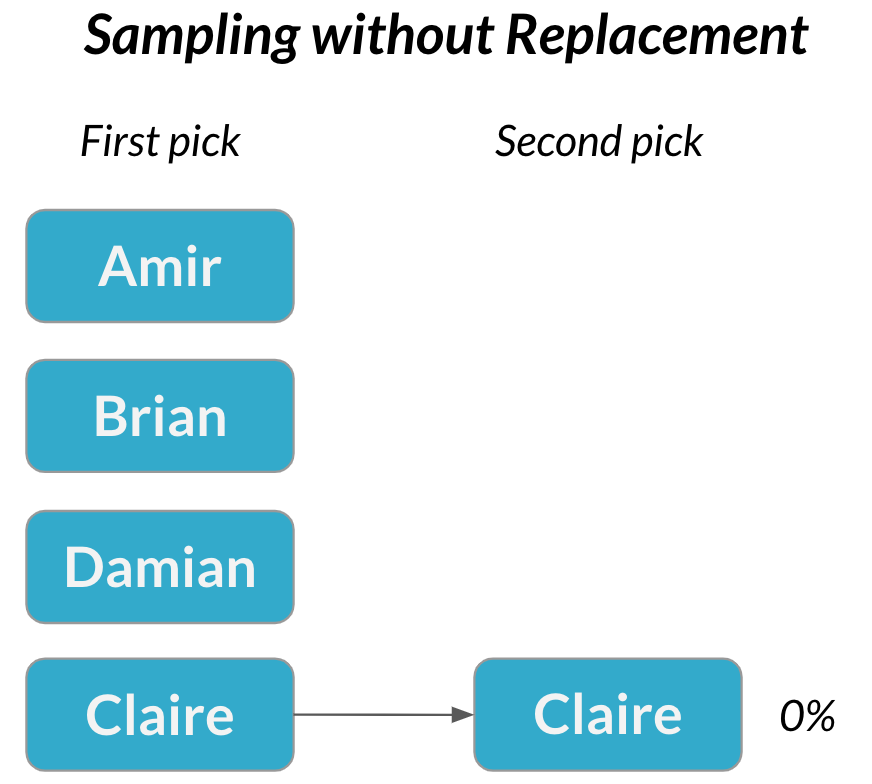
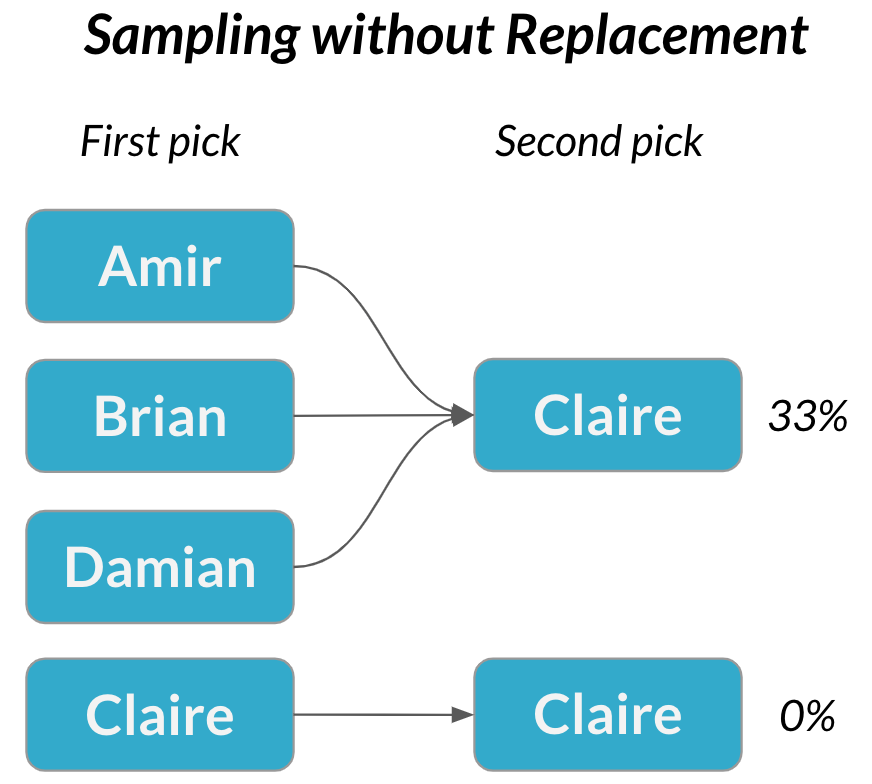
Échantillonnage sans remise

Une deuxième réunion
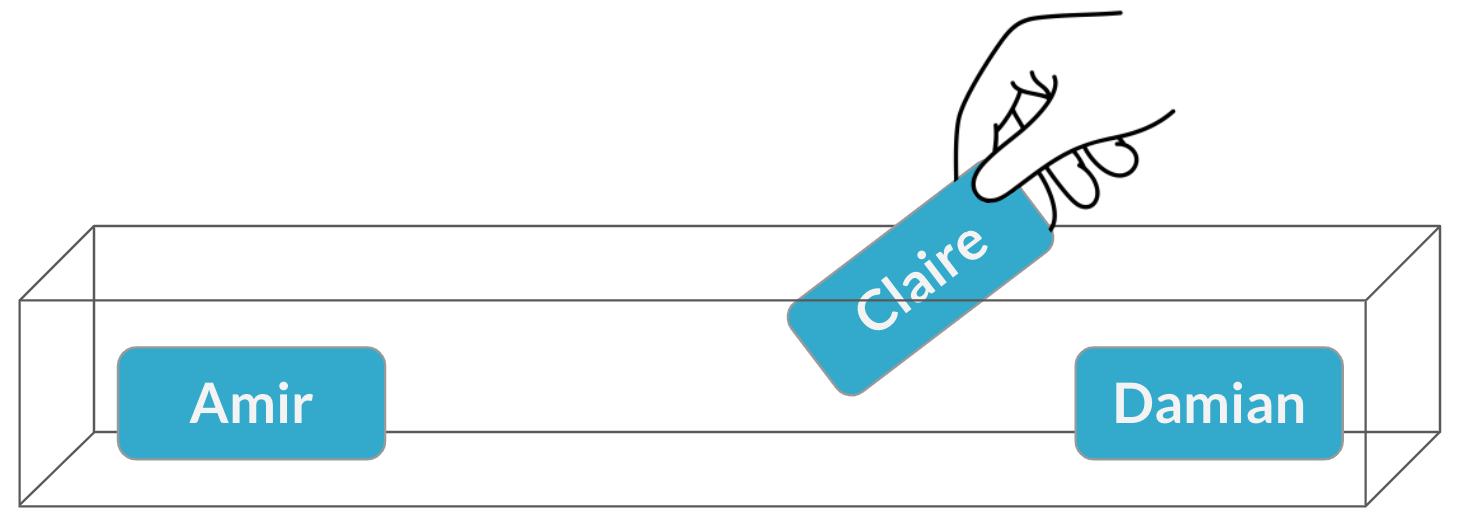
$$P(\text{Claire}) = \frac{1}{3} = 33 \%$$
Échantillonner deux fois en Python
sales_counts.sample(2)
name n_sales
1 Brian 128
2 Claire 75
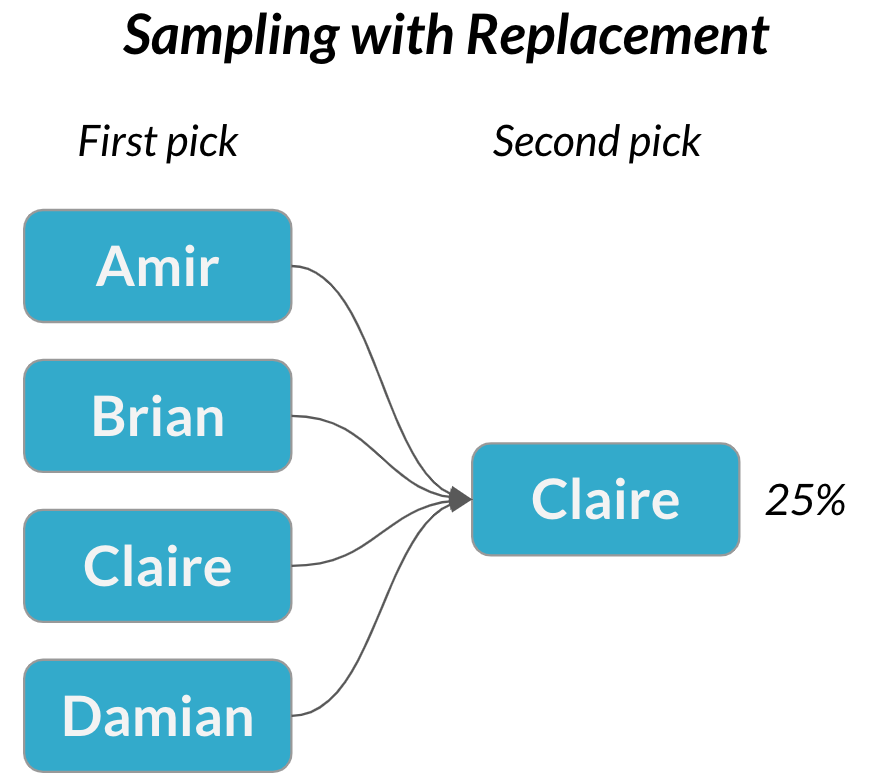
Échantillonnage avec remise
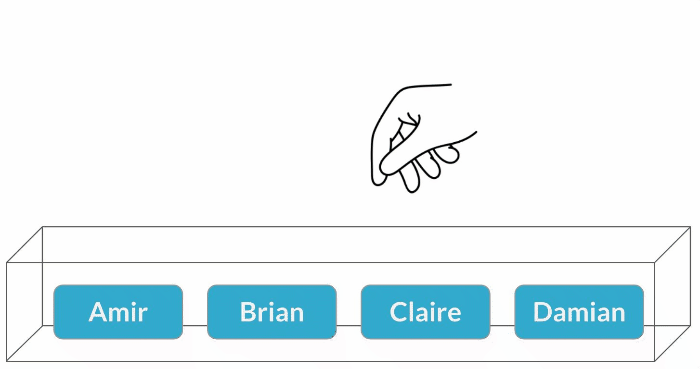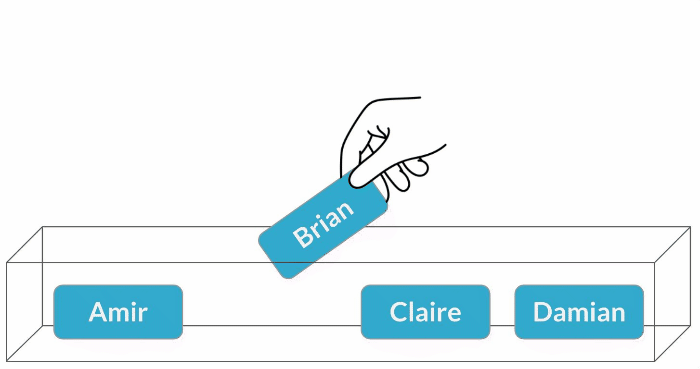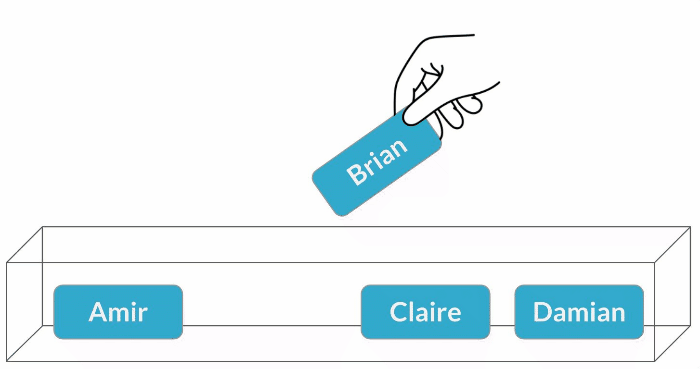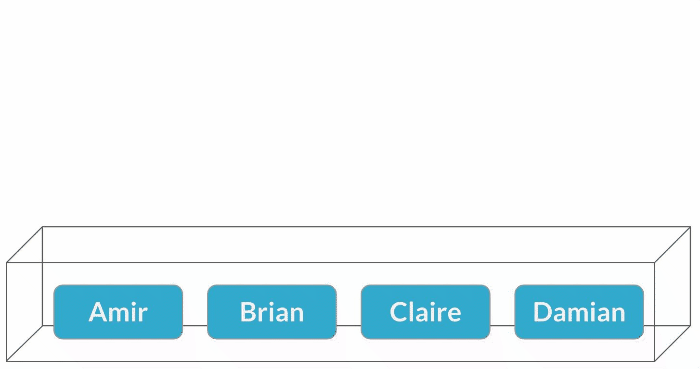
Échantillonnage avec remise
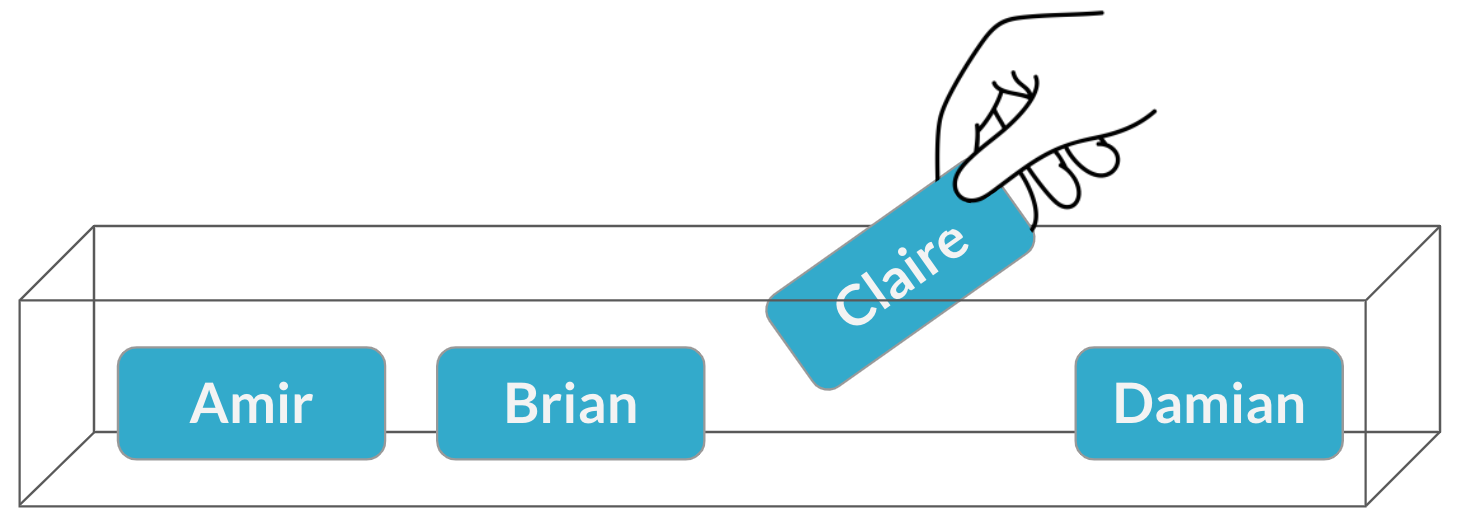
$$P(\text{Claire}) = \frac{1}{4} = 25 \%$$
Echantillonnage avec/sans remise en Python
sales_counts.sample(5, replace = True)
name n_sales
1 Brian 128
2 Claire 75
1 Brian 128
3 Damian 69
0 Amir 178
Événements indépendants
Deux événements sont indépendants si la probabilité du deuxième événement n’est pas affectée par le résultat du premier.

Événements indépendants
Deux événements sont indépendants si la probabilité du deuxième événement n’est pas affectée par le résultat du premier.
Échantillonnage avec remise : chaque choix est indépendant
Événements dépendants
Deux événements sont dépendants si la probabilité du deuxième événement est affectée par le résultat du premier.

Événements dépendants
Deux événements sont dépendants si la probabilité du deuxième événement est affectée par le résultat du premier.
Événements dépendants
Deux événements sont dépendants si la probabilité du deuxième événement est affectée par le résultat du premier.
Échantillonnage sans remise : les choix deviennent dépendants
Passons à la pratique !
Introduction aux statistiques en Python

